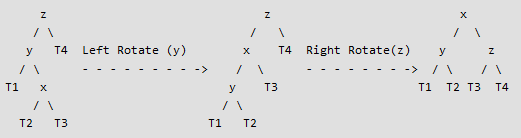Memory allocator
Allocating memory with malloc is usually quite efficient. However, for performance-critical applications that need to allocate/free many objects of the same size, the genericity of malloc may become a burden.
The goal of this exercise is to implement a fast allocator that provides a high-performance memory allocation mechanism for objects of a fixed-size.
To use this allocator, an application first initializes a struct fast_alloc structure by calling void fast_alloc_init(struct fast_alloc*fa, size_t block_size). This pre-allocates a number (e.g. 100) of objects of size block_size and it creates a linked-list of available blocks.
When the application needs a new object, it calls void* fast_alloc(struct fast_alloc *fa) which simply extracts the first block of the list of available blocks.
When the application frees an object with void fast_free(struct fast_alloc *fa, void* ptr), the memory allocator simply adds the block at the beginning of the list of available blocks.
Preparation
To get started, get the base for today's lab:
- git clone -b tp7_memalloc_base https://gitlabev.imtbs-tsp.eu/csc4508/csc4508_facebook.git csc4508_tp7
- or git checkout tp7_memalloc_base
Implementing a memory allocator
Implement void fast_alloc_init(struct fast_alloc *fa, size_t block_size). This function initializes the fa structure. It allocates 10 objects of size block_size and creates a linked list that starts at fa->firstblock.
Implement void* fast_alloc(struct fast_alloc *fa). This function removes the first token of the linked list and returns its address.
If the list is empty, print an error message ("Cannot allocate memory") and return NULL.
Implement void fast_free(struct fast_alloc *fa, void* ptr). This function adds the block located at address ptr to the list of available blocks.
We evaluate the performance of the memory allocator by performing many calls to malloc/free. Compare the performance obtained with libc's memory allocator (i.e. malloc and free) and with your fast allocator.
Thread-safety
- Add a synchronization mechanism (e.g. a mutex) to ensure the consistency of the linked list
- Use one instance of the memory allocator per thread to avoid concurrent access to the memory allocator
Implement and evaluate both strategies. Modify the benchmarking program so that it creates multiple threads that run the benchmark in parallel.
How does the performance of both strategies compare with the performance of malloc ?
FaceBook (bonus)
As the number of users increases, the FaceBook server faces an increase in the number of connection to process every second. To absorb this increase, one solution is to speed up the treatment of some pages.
For this, we will set up a cache system memory inspired by memcached. the principle is to store in memory the content of a page which can be reused later. For example, the profile page of a user can be kept in memory, then reused as it is as long as its profile is not modified.
Preparation
To get started, get the base for today's lab:
- git clone -b tp7_base https://gitlabev.imtbs-tsp.eu/csc4508/csc4508_facebook.git csc4508_tp7
- or git checkout tp7_base
Implementing a binary search tree
The cache that we are going to set up associates a key (for example, the requested URL) with a data (for example, the content of the page to display). The different (key, value) couples are stored as a binary search tree ordered by the key.
The goal of this exercise is to implement an AVL tree ( tree by Georgy Adelson-Velsky and Landis ) which has the property of being self-balanced. In an AVL tree, the height of two child trees of any node differs by at most 1. If their height differs by more than one, a rebalancing is triggered.
This guarantees a search complexity of log2(n), n being the number of nodes.
For example, the tree in figure 1 is an AVL tree, because, for each node, the height difference between the left subtree and the right subtree is less than or equal to 1.
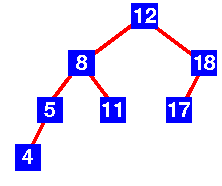
Figure 1: example of an AVL tree
On the other hand, the tree in figure 2 is not an AVL tree. Indeed, for node 12, the height of the left subtree is 4, while the height of the right subtree is 2.
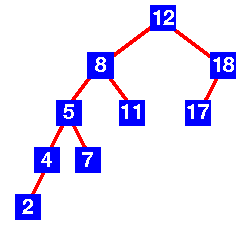
Figure 2: example of a non-AVL tree
In this exercise, you will implement an AVL tree that we will use to store key / value pairs like the Dictionary class from Java or std::map from the C ++ STL.
The memcache directory contains a set of functions that will serve as a basis for the implementation of this tree.
In treeAVL.c, complete all the TODO in updateHeight(), nbNodes(), newNode(), and insert(). Do not mind the release() function for now.
NB: Do not worry about making the tree balanced (the insert
function therefore does not implement, for the moment,
self-balancing) or storing the value associated with each key. Also, your
function insert shall work as follows:
- If node is NULL, then insert returns newNode(key)
- If key is smaller than node->key,
insert inserts key in the lowest possible
leaf of the left subtree of node.
To do this, we recommend that you call recursively insert. NB: the insert() function returns a struct node *. Also, don't forget to store the node returned by insert() in your structure data (don't just call insert() regardless of its return value. Otherwise, you will probably encounter some bugs in this question or to the following questions).
- If key is greater than node->key,
then insert key in the lowest leaf of the
right subtree of node.
To do this, we recommend that you call recursively insert. Same NB as in the previous point.
- If key is equal to node->key, insert simply returns node without doing anything else (thus, there are never two identical keys in the tree).
- Then, insert updates the height field of node .
Once your functions are implemented, type make run. If needed, fix your functions until make run prints:
In other words, the test_insert_and_nbNode unit test is OK.
Now run make valgrind which runs the program with Valrgind. Valgrind at least informs you that you have memory leaks. Complete release() and possibly the other functions coded so far so that valgrind ./unitTests does not notify you of any memory access problem or memory leak.
So, test_insert_and_nbNode and test_release are OK.
Implementing getKeyNode()
Implement the internal getKeyNode() function which allows you to search for a key in the tree. Do not forget to check for memory access problem or memory leaks with valgrind.
This question aims to implement the balancing of the tree that happens during insertion.
To do this, once the insertion has been completed, for each node concerned by the insertion, it is necessary to calculate its "balance", i.e. the height difference between the left subtree of the node and its right subtree.
If the balance of a node is between -1 and +1, there is nothing to do.
On the other hand, if the balance of a node is strictly less than -1 or strictly greater than +1, it is necessary to rebalance the tree at this node. 4 different cases may happen (to be processed in the insert() function after the balance calculation). When presenting these 4 cases, 3 nodes play a particular role:
- z is the deepest node at which the balance is strictly less than -1 or
strictly greater than +1;
- x is the grandchild node of z, whose tree contains the key that was just
inserted;
- y is the child node of z, which is the parent of x.
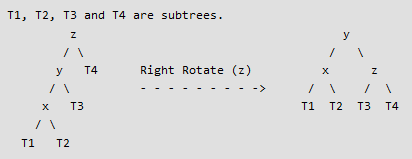
1st case - Left-Left case : At the level of z, the tree is unbalanced to the left. In addition, x is located to the left of y. In order to rebalance the tree, rotate z to the right (see figure 3).
2nd case - Right-Right Case : At the level of z, the tree is unbalanced to the right. In addition, x is located to the right of y. So, to rebalance the tree, rotate z to the left (see figure 4).
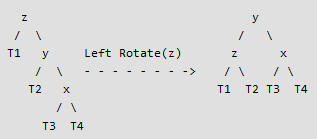
3rd case - Left-Right Case : At the level of z, the tree is unbalanced on the left. Moreover, x is located to the right of y. So to rebalance the tree, first rotate y to the left, then rotate z to the right (see figure 5).
4th case - Right-Left Case : At the level of z, the tree is unbalanced to the right. Moreover, x is to the left of y. Then, to rebalance the tree, first rotate y to the right, then rotate z to the left (see figure 6).
Managing these 4 cases for this node is enough to rebalance the entire tree, because the tree returns to its original height.
The rightRotate and leftRotate functions are provided. Add the calculation of the balance and the treatment of the 4 cases in the insert() function.
Then, run make run . Fix your function until:
- the tests left_balance_test , RightRight_balance_test, leftRight_balance_test and LeftRight_balance_test are OK;
- valgrind ./unitTests do not report any memory access or memory leak problem.
Storage of key / value pairs in the AVL tree
So far, our AVL tree only stores keys. This question aims at usubf this tree to store key / value pairs, and thus obtain a dictionary structure (cf. classes Dictionary in Java or std::map in the STL C ++). This allows us to find the value associated with a key with a complexity of O(log(n)).
Complete treeAVL.h and treeAVL.c:
- add a char *value field to the structure Node;
- add a char *value parameter to the newNode function and copy its content into the string node value character created;
- add a char *value parameter to the insert function and use this parameter in this function. In particular, if there is already a node with key key, be sure to replace the old value with the new value;
- Complete the getValue() function
NB: it is probable that the search algorithm in getValue() is very similar to the search algorithm in getKeyHeight(). To avoid code duplication, create a function which centralizes this code and which is called by getValue() and getKeyHeight().
Take into account, in the unit tests unitTest_usernameUnix.c, the new signature of the insert() function by running the following commands in a terminal:
As a precaution, check that the changed lines went well by running
You should only have lines like this:
in other words, only lines mentioning line numbers (like 38c38 above) or "---". If not, do
cp /tmp/unitTests_$USER.c .
in order to recover your initial file. Then, post an SOS message on the forum.
Finally, type make run . Fix your functions until:
- the test test_getValue is OK;
- code> valgrind ./unitTests does not notify you of any memory access or leak memory problem.
Implementing a cache
- void memcache_init(struct memcache_t* cache): initialize the cache
- void memcache_set(struct memcache_t* cache, const char* key, void* value) : add the couple (key, value) to the cache
- void* memcache_get(struct memcache_t* cache, const char* key): returns the value associated with the key key
Once integrated into the FaceBook server, the cache may be used by several threads simultaneously. It is therefore necessary to protect it against concurrent accesses.
Modify your implementation to manage concurrent access while limiting contention problems.
Using the cache in FaceBook
In order to speed up the display of certain pages, we are going to use the cache by associating a URL (for example "view_user?user=0") to a response (in this case, the page displayed for the user 0).
Caching do_help
First, we will start with the caching of the do_help function. Edit this function as follows:
- If the page_request->url key is in the cache, copy the associated value into page_request->reply and exit the function ;
- Otherwise, allocate a struct page_reply and fill it with the content of the page ;
- Add the (key, value) couple in the cache.
To test your implementation, it is recommended to add messages indicating whether the page is generated or copied from the cache. You can also simulate a complex calculation necessary for the generation of the page by adding a call to sleep().
Caching do_hello
Do the same for the do_hello function.
Caching do_view_user
The do_view_user function is slightly more complex to implement. Indeed, the content displayed may change when the profile of the user is changed.
A solution to this problem is to add a timestamp to the cached page and the user profile. If the user timestamp is newer than the cached timestamp, it is necessary to update the cached data.
Implement this solution in the do_view_user function.
- add a last_modified field of type struct timeval in the user structure. Whenever a user changes, update this field by calling gettimeofday();
- Define a struct reply structure containing an array of reply characters and a timestamp.
- In the do_view_code function, if the response timestamp is older as the user timestamp, regenerate the page and update the timestamp.