Tri rapide (∼1h15 – moyen – entraînement)
L'algorithme de tri rapide (quick sort en anglais) est un des algorithmes de tri les plus efficaces connus : c'est un algorithme qui a une complexité moyenne optimale, même si cet algorithme peut devenir inefficace dans des cas pathologiques. De plus, l'algorithme de tri rapide est un algorithme de tri en place, c'est-à-dire qu'il ne nécessite pas de tableau annexe pour trier les éléments. L'algorithme de tri fusion que vous avez étudié dans l'exercice précédent a aussi une complexité moyenne optimale, mais il nécessite un tableau annexe, ce qui rend le tri rapide plus efficace en pratique.
L'algorithme de tri rapide part aussi de l'idée qu'il faut diviser pour mieux régner. Toutefois, contrairement au tri rapide, lorsque l'algorithme de tri rapide divise le tableau en deux parties, le tri rapide s'assure que tous les éléments du tableau de gauche sont plus petits que tous les éléments du tableau de droite. Au final, il n'y a donc pas besoin de fusionner les tableaux comme dans le tri fusion puisque les tableaux de gauche et de droite sont déjà bien placés.
Pour y arriver, le tri rapide choisit un élément appelé pivot dans le tableau. Le choix de ce pivot est libre, mais on prend en général l'élément le plus à droite du tableau. Ensuite, l'algorithme place ce pivot à sa place définitive en s'assurant que tous les éléments à gauche du pivot sont plus petits que le pivot et que tous les éléments à droite du pivot sont plus grands. On peut remarquer que, comme le pivot est choisit de façon arbitraire, le tableau de gauche et le tableau de droite ont une taille quelconque. À l'étape suivante, on trie de façon récursive les tableaux de gauche et de droite.
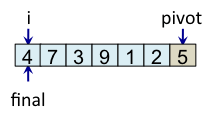
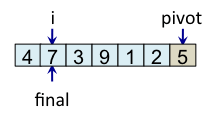
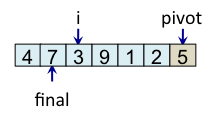
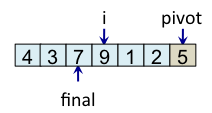
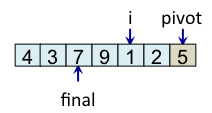
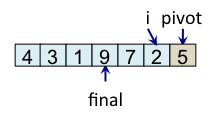
Le schéma ci-dessous illustre l'étape de partitionnement. Après avoir choisit l'élément de droite comme pivot, c'est-à-dire l'élément 5, l'algorithme initialise i et final à 0. L'indice i sert à parcourir le tableau alors que l'indice final sert à savoir quelle sera la place finale du pivot.
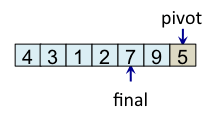
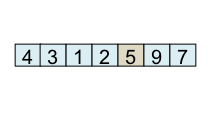
Le principe de l'algorithme est de n'incrémenter final qu'après s'être assuré que l'élément à la place final (et donc tous les éléments à gauche de final) est strictement plus petit que le pivot. Par exemple, lorsque i est égal à 1, l'élément à l'indice final (7) est plus grand que le pivot (5), donc l'algorithme n'incrémente pas final. En revanche, dès que l'algorithme s'aperçoit qu'un élément pourrait être bien placé en échangeant des éléments, l'algorithme incrémente final. C'est, par exemple, le cas lorsque i est égal à 2. Dans ce cas, l'élément à la place final vaut 7, l'élément à la place i vaut 3 et l'élément pivot vaut 5. Comme 3 est plus petit que 5, il suffit d'inverser 3 et 7 pour que l'élément à la place final devienne strictement plus petit que le pivot. Une fois cette inversion effectuée, on peut incrémenter final puisque 3 est maintenant bien placé. À la fin de l'étape de partitionnement, on est assuré que les éléments à gauche de final sont strictement plus petits que le pivot, alors que les éléments à droite de final sont plus grands ou égaux. Il suffit alors de déplacer le pivot à la place final, comme illustré à l'étape fin, puis de trier les tableaux de gauche et de droite.
| i=0 |
|
Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final |
| i=1 |
|
Teste si tab[i] < pivot faux => ne fait rien |
| i=2 |
|
Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final |
| i=3 |
|
Teste si tab[i] < pivot faux => ne fait rien |
| i=4 |
|
Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final |
| i=5 |
|
Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final |
| i=6 |
|
i atteint pivot => échange pivot avec tab[final] |
| Fin |
|
État à la fin du partitionnement Ce qui est à gauche du pivot est plus petit que ce qui est à droite |
Une illustration folklorique de l'algorithme est donnée ici.
Écrivez une méthode quicksort prenant en argument un tableau d'entiers et deux indices nommés start et end. Cette méthode doit trier récursivement le tableau se trouvant entre start et end inclus.
- Si la différence entre end et start est inférieur ou égale à zéro, le tableau à une taille inférieure ou égale à 1, ce qui signifie que le sous-tableau est trié. Il ne faut donc rien faire.
- Sinon, c'est que le tableau a une taille au moins égale à deux. La méthode doit
donc :
- Appeler partition pour partitionner le tableau et stocker l'indice final dans une variable locale,
- Appeler quicksort avec la partie gauche du tableau (entre start et final - 1) et quicksort avec la partie droite du tableau (entre final + 1 et end).
Testez votre méthode quicksort en appelant quicksort(tab, 0, tab.length - 1) dans votre méthode main. Vérifiez que le tableau est bien trié en appelant display.
Finalement, écrivez une seconde méthode quicksort ne prenant qu'un tableau d'entiers en argument, et appelant la seconde méthode quicksort de façon à trier entièrement le tableau passé en argument.
