CI2 : Les méthodes de classe
Dans cette série d'exercices, vous apprenez à utiliser les méthodes statiques et vous étudiez des algorithmes classiques de recherche et de tri.
Durée des exercices obligatoires : 2h10 en présentiel
- Exercice 1 : obligatoire (moyen, ∼1h)
- Exercice 2 : obligatoire (moyen, ∼1h10)
- Exercice 3 : entraînement (moyen, ∼1h10)
- Exercice 4 : entraînement (moyen)
Palindromes et anacycliques (∼60mn – moyen – obligatoire)
Le but de cet exercice est de vous familiariser avec les méthodes de classes en travaillant sur des tableaux de caractères.
Créez une variable words initialisé avec les tableaux de caractères suivants :
- { 'a', 'n', 'i', 'm', 'a', 'l' },
- { 'r', 'a', 'd', 'a', 'r' },
- { 'r', 'e', 's', 'u', 'm', 'a' },
- { 'r', 'e', 's', 's', 'a', 's', 's', 'e', 'r' },
- { 'r', 'e', 'l', 'a', 'c', 'e', 'r' },
- { 'k', 'a', 'y', 'a', 'k' },
- { 'v', 'i', 'v', 'e', ' ', 'J', 'a', 'v', 'a', ' ', '!' }
On vous rappelle que pour copier/coller sous Linux, il faut sélectionner à la souris la zone que vous souhaitez copier, puis cliquer sur le bouton du milieu de la souris pour coller.
Le tableau words est donc un tableau de (références vers des) tableaux de caractères, dont le type est naturellement char[][].
La déclaration et l'initialisation d'un tableau de tableau s'écrit :
Pour afficher un caractère, il suffit d'utiliser System.out.print(char c) (sans retour à la ligne) ou System.out.println(char c) (avec retour à la ligne). Notez que System.out.println(char c) est une surcharge de System.out.println(String msg) que vous avez déjà utilisé. Vous pouvez aussi utiliser System.out.println() sans paramètre, qui est une troisième surcharge et qui génère uniquement un retour à la ligne sans rien afficher de plus.
Pensez à utiliser la documentation Java (voir menu Liens utiles). Par exemple, vous pouvez voir les méthodes qui permettent d'effectuer des affichages dans le terminal ici.
Écrivez une méthode de classe nommée printWords(char[][] words) utilisant printWord pour afficher chacun des tableaux de caractères référencés par words. Utilisez ensuite cette méthode pour afficher les éléments du tableau words à partir de la méthode main.
Écrivez une méthode isPalindrome(char[] word) renvoyant vrai si le mot référencé par word est un palindrome et faux sinon. On vous rappelle qu'un palindrome est un mot qui reste identique si l'on inverse l'ordre des lettres. C'est par exemple le cas du mot « radar ».
Vous pouvez tester la méthode isPalindrome en affichant son résultat lorsque vous l'invoquez avec words[0] (résultat attendu faux) et avec words[1] (résultat attendu vrai).
Pour mettre en œuvre cet algorithme, vous pouvez par exemple parcourir la première moitié du mot (de 0 à word.length/2) avec une variable entière i, et vérifier que pour tout i, word[i] est égal à word[word.length - i - 1].
On cherche maintenant à trouver les anacycliques dans notre tableau de mots. Un anacyclique est un mot qui peut se lire dans les deux sens (aux accents près). Contrairement à un palindrome, lorsqu'on lit un anacyclique de droite à gauche, le mot résultant n'est pas forcément le même que celui obtenu en lisant de gauche à droite. De façon à trouver les anacycliques dans notre liste de mot, on va les réécrire en inversant l'ordre des lettres.
Pour commencer, on vous demande d'écrire une méthode reverseWord(char[] word) qui inverse les lettres dans le tableau word (c'est-à-dire, la lettre à la position i est inversée avec la lettre à la position word.length - i - 1). Vous remarquerez que, comme word est passé par référence, le mot référencé par l'appelant est bien modifié.
Testez votre méthode en inversant le mot words[0] dans la méthode main. Pensez à afficher le mot inverse avec la méthode printWord.
Pour finir, écrivez une méthode reverseWords(char[][] list) qui inverse l'ordre des lettres de chacun des mots référencés par list. Quels mots et phrases sont des anacycliques ?
Tous les mots, sauf le dernier, sont des anacycliques.
Tri fusion (∼1h10 – moyen – obligatoire)
Le tri étant décidément une réelle passion chez les informaticiens, nous allons étudier un nouvel algorithme de tri appelé l'algorithme de tri fusion (merge sort en anglais). Cet algorithme est intéressant car il peut être mis en œuvre de façon relativement efficace.
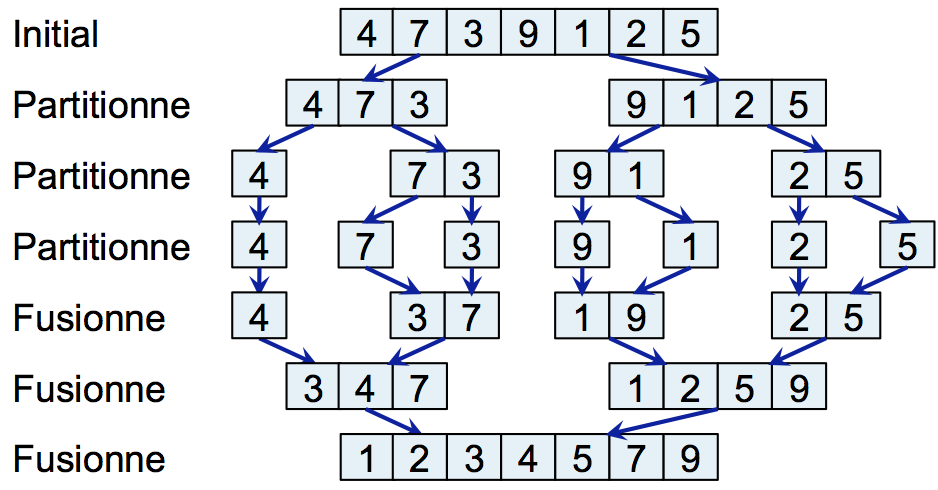
L'algorithme de tri fusion part de l'idée qu'il faut diviser pour mieux régner. Le principe est de prendre un tableau non trié et de le partitionner en deux parties à peu près égales. Ensuite, de façon récursive, l'algorithme trie le tableau de gauche et le tableau de droite. Enfin, l'algorithme fusionne les deux tableaux triés pour construire un tableau contenant tous les éléments triés. Cette opération de fusion est une opération relativement efficace car fusionner des tableaux triés est rapide en terme de temps de calcul.
Le schéma suivant illustre le principe. De façon récursive, l'algorithme commence par partitionner les tableaux jusqu'à obtenir des tableaux de taille 1. Ce tableau de taille 1 est naturellement trié. Ensuite, l'algorithme fusionne les tableaux de façon à reconstruire la liste triée.
La mise en œuvre que nous vous proposons dans cet exercice n'est pas optimisée, mais elle a l'avantage d'être relativement simple à comprendre. Cette mise en œuvre est subdivisée en trois parties. Dans la première partie, nous écrivons la méthode qui fusionne des tableaux triés. Dans la second partie, nous écrivons la méthode qui partitionne les tableaux. Enfin, dans la troisième partie nous complétons notre programme en utilisant les deux méthodes précédentes.
Une illustration fantaisiste de l'algorithme est donnée ici.
Nous pouvons maintenant mettre en œuvre la fusion. Pour cela, vous allez écrire une nouvelle méthode nommée merge, prenant en argument deux tableaux t1 et t2 triés et renvoyant la fusion de ces deux tableaux. Le fait qu'il y ait deux méthodes merge ne pose pas de problème, car les arguments des deux méthodes sont différents, ce qui permet à Java de savoir quelle méthode on souhaite appeler en fonction des paramètres.
Nous mettons en œuvre merge de façon récursive :
- Si t1 a une taille égale à zéro, alors merge doit renvoyer t2
- Si t2 a une taille égale à zéro, alors merge doit renvoyer t1
- Si t1[0] est plus petit que ou égal à t2[0], alors merge doit renvoyer le tableau construit à partir de t1[0] et du résultat de la fusion de la partie droite de t1 avec le tableau t2. La partie droite de t1 s'obtient en appelant la méthode right et l'ajout à gauche de t1[0] s'obtient en appelant la seconde méthode merge que vous avez défini à la question précédente.
- Dans le cas inverse, il suffit d'appeler merge en inversant les rôles de t1 et t2.
Testez merge en affichant le résultat de la fusion de t1 et t2 dans la méthode main.
Les deux cas les plus couteux sont les deux derniers. On note que le dernier cas se produit au maximum n fois. L'avant-dernier cas nous donne la relation de récurrence suivante:
Où le n vient de right et int[] merge(int val, int[] tab). On appelle ensuite merge avec un élément en moins dans un des tableaux. À partir de là, nous avons:
La complexité finale de merge est donc quadratique.
- Création du tableau final de taille égale à la somme des deux tailles.
- Pour chacune des deux tableaux t0 et t1, nous conservons indice i0 et i1 nous indiquant notre position dans chaque tableau. Ces indices sont initialisés à 0 et seront incrémenté de 1 à chaque fois qu'un élément sera ajouté au tableau final.
- Tant que les deux indices ne sont pas égaux à la taille de leur tableau respectif, prendre la valeur la plus petite entre t0[i0] et t1[i1] et la rajouter au tableau final. Incrémenter la valeur de l'indice ayant amené l'ajout.
Dans cette partie, nous nous occupons de partitionner un tableau.
Nous pouvons enfin mettre en œuvre l'algorithme du tri-fusion.
- Si tab a une taille inférieure ou égale à 1, alors le tableau est déjà trié et il suffit de le renvoyer.
- Sinon, il faut appeler mergeSort sur la partie gauche de tab, puis mergeSort sur la partie droite de tab et enfin utiliser merge pour fusionner les résultats des deux appels à mergeSort.
On rappelle que :
En réalité, la complexité avec un merge efficace est , ce qui est la complexité optimale pour un algorithme de tri ! En effet, la relation de récurrence devient : Le log vient du fait que l'on divise n par deux jusqu'à obtenir un nombre inférieur à 1.
Tri rapide (∼1h15 – moyen – entraînement)
L'algorithme de tri rapide (quick sort en anglais) est un des algorithmes de tri les plus efficaces connus : c'est un algorithme qui a une complexité moyenne optimale, même si cet algorithme peut devenir inefficace dans des cas pathologiques. De plus, l'algorithme de tri rapide est un algorithme de tri en place, c'est-à-dire qu'il ne nécessite pas de tableau annexe pour trier les éléments. L'algorithme de tri fusion que vous avez étudié dans l'exercice précédent a aussi une complexité moyenne optimale, mais il nécessite un tableau annexe, ce qui rend le tri rapide plus efficace en pratique.
L'algorithme de tri rapide part aussi de l'idée qu'il faut diviser pour mieux régner. Toutefois, contrairement au tri rapide, lorsque l'algorithme de tri rapide divise le tableau en deux parties, le tri rapide s'assure que tous les éléments du tableau de gauche sont plus petits que tous les éléments du tableau de droite. Finalement, il n'y a donc pas besoin de fusionner les tableaux comme dans le tri fusion puisque les tableaux de gauche et de droite sont déjà bien placés.
Pour y arriver, le tri rapide choisit un élément appelé pivot dans le tableau. Le choix de ce pivot est libre, mais on prend en général l'élément le plus à droite du tableau. Ensuite, l'algorithme place ce pivot à sa place définitive en s'assurant que tous les éléments à gauche du pivot sont plus petits que le pivot et que tous les éléments à droite du pivot sont plus grands. On peut remarquer que, comme le pivot est choisi de façon arbitraire, le tableau de gauche et le tableau de droite ont une taille quelconque. À l'étape suivante, on trie de manière récursive les tableaux de gauche et de droite.
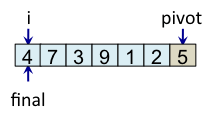
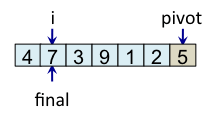
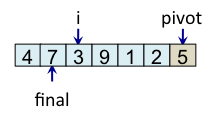
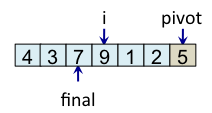
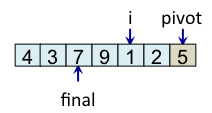
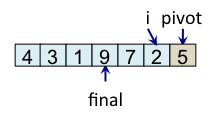
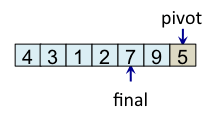
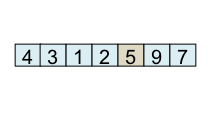
Le schéma ci-dessous illustre l'étape de partitionnement. Après avoir choisi l'élément de droite comme pivot, c'est-à-dire l'élément 5, l'algorithme initialise i et final à 0. L'indice i sert à parcourir le tableau alors que l'indice final sert à savoir quelle sera la place finale du pivot.
Le principe de l'algorithme est de n'incrémenter final qu'après s'être assuré que l'élément à la place final (et donc tous les éléments à gauche de final) est strictement plus petit que le pivot. Par exemple, lorsque i est égal à 1, l'élément à l'indice final (7) est plus grand que le pivot (5), donc l'algorithme n'incrémente pas final. En revanche, dès que l'algorithme s'aperçoit qu'un élément pourrait être bien placé en échangeant des éléments, l'algorithme incrémente final. C'est, par exemple, le cas lorsque i est égal à 2. Dans ce cas, l'élément à la place final vaut 7, l'élément à la place i vaut 3 et l'élément pivot vaut 5. Comme 3 est plus petit que 5, il suffit d'inverser 3 et 7 pour que l'élément à la place final devienne strictement plus petit que le pivot. Une fois cette inversion effectuée, on peut incrémenter final puisque 3 est maintenant bien placé. À la fin de l'étape de partitionnement, on est assuré que les éléments à gauche de final sont strictement plus petits que le pivot, alors que les éléments à droite de final sont plus grands ou égaux. Il suffit alors de déplacer le pivot à la place final, comme illustré à l'étape fin, puis de trier les tableaux de gauche et de droite.
Une illustration folklorique de l'algorithme est donnée ici.
Écrivez une méthode quicksort prenant en argument un tableau d'entiers et deux indices nommés start et end. Cette méthode doit trier récursivement le tableau se trouvant entre start et end inclus.
- Si la différence entre end et start est inférieur ou égale à zéro, le tableau à une taille inférieure ou égale à 1, ce qui signifie que le sous-tableau est trié. Il ne faut donc rien faire.
- Sinon, c'est que le tableau a une taille au moins égale à deux. La méthode doit
donc :
- Appeler partition pour partitionner le tableau et stocker l'indice final dans une variable locale,
- Appeler quicksort avec la partie gauche du tableau (entre start et final - 1) et quicksort avec la partie droite du tableau (entre final + 1 et end).
Testez votre méthode quicksort en appelant quicksort(tab, 0, tab.length - 1) dans votre méthode main. Vérifiez que le tableau est bien trié en appelant display.
Finalement, écrivez une seconde méthode quicksort ne prenant qu'un tableau d'entiers en argument, et appelant la seconde méthode quicksort de façon à trier entièrement le tableau passé en argument.
En créant l'équation de récurrence dans ce cas, on retrouve la même que pour le tri fusion vu plus haut (en sachant que la méthode partition est linéaire). On retrouve donc une complexité de .
Le pire des cas se produit quand le tableau est déjà trié. Dans ce cas, la fonction partition ne fait rien, mais a quand même un coup linéaire. L'équation de récurrence devient : La complexité est donc quadratique en la taille du tableau.
Cependant, cette solution n'est pas adaptée, car trouver la médiane n'est pas gratuit ! Un algorithme trivial trouve la médiane en temps quadratique (un algorithme optimal trouve la médiane en temps linéaire, mais c'est très compliqué).
Mise en pratique des tris (entraînement)
- Exemple 1. Entrée : {4, 2, 4}, Sortie : 4
- Exemple 2. Entrée : {8, 8, 2, 8, 2, 2, 1, 8, 8}, Sortie : 8
- Exemple 1. Entrée : {2, 5, 3, 19, 42}, Sortie : false
- Exemple 2. Entrée : {1, 4, 3, 4, 19}, Sortie : true
Étant donné un tableau d'entiers représentant les citations d'un ou une scientifique, écrire une fonction calculant son h-index.
- Exemple 1. Entrée : {2, 0, 13, 24}, Sortie : 2
- Exemple 2. Entrée : {12, 6, 7, 13}, Sortie : 4
- Exemple 3. Entrée : {1, 38, 12, 3}, Sortie : 3