CSC 3101 – Algorithmique et langage de programmation

Tri fusion (∼1h10 – moyen – obligatoire)

Le tri étant décidément une réelle passion chez les informaticiens, nous allons étudier un nouvel algorithme de tri appelé l'algorithme de tri fusion (merge sort en anglais). Cet algorithme est intéressant car il peut être mis en œuvre de façon relativement efficace.

L'algorithme de tri fusion part de l'idée qu'il faut diviser pour mieux régner. Le principe est de prendre un tableau non trié et de le partitionner en deux parties à peu près égales. Ensuite, de façon récursive, l'algorithme trie le tableau de gauche et le tableau de droite. Enfin, l'algorithme fusionne les deux tableaux triés pour construire un tableau contenant tous les éléments triés. Cette opération de fusion est une opération relativement efficace car fusionner des tableaux triés est rapide en terme de temps de calcul.

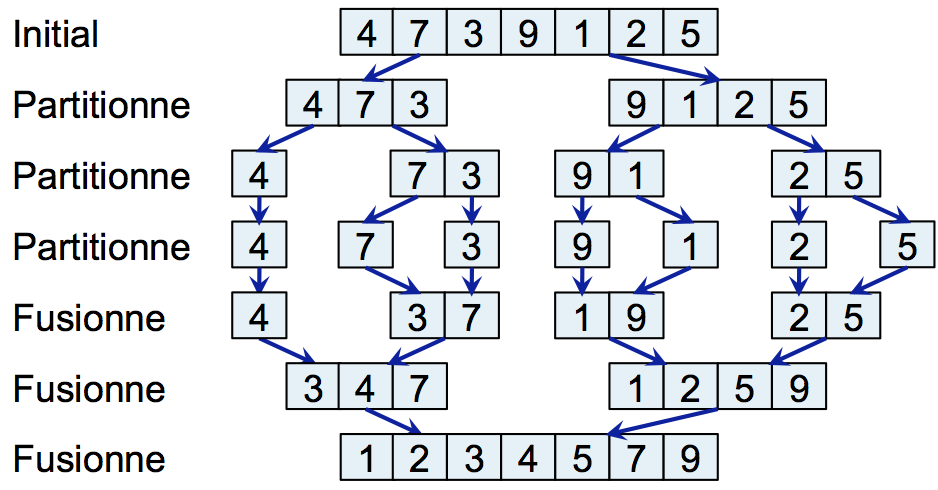
Le schéma suivant illustre le principe. De façon récursive, l'algorithme commence par partitionner les tableaux jusqu'à obtenir des tableaux de taille 1. Ce tableau de taille 1 est naturellement trié. Ensuite, l'algorithme fusionne les tableaux de façon à reconstruire la liste triée.

Principe du tri fusion.

La mise en œuvre que nous vous proposons dans cet exercice n'est pas optimisée, mais elle a l'avantage d'être relativement simple à comprendre. Cette mise en œuvre est subdivisée en trois parties. Dans la première partie, nous écrivons la méthode qui fusionne des tableaux triés. Dans la second partie, nous écrivons la méthode qui partitionne les tableaux. Enfin, dans la troisième partie nous complétons notre programme en utilisant les deux méthodes précédentes.

Une illustration fantaisiste de l'algorithme est donnée ici.

la fusion

Créez un projet nommé msort contenant une classe MergeSort, elle-même contenant une méthode main. Allouez le tableau d'entiers t1 initialisé avec les valeurs 3, 4, 7 et le tableau d'entiers t2 initialisé avec les valeurs 1, 2, 5, 9.

Écrivez une méthode display prenant en argument un tableau d'entiers et l'affichant dans le terminal. Vérifiez que votre méthode est correcte en l'appelant avec l'argument t1.

Avant de pouvoir fusionner les deux tableaux, nous avons besoin de deux méthodes annexes. La première méthode, nommée int[] right(int[] tab), alloue un tableau de taille tab.length - 1. Elle copie les éléments de droite du tableau tab (c.à-d., à partir de l'élément d'index 1) dans le tableau alloué et renvoie ce nouveau tableau. De façon à tester la méthode right, appelez la dans la méthode main avec l'argument t1, et vérifiez, en affichant le résultat de right avec display, que le nouveau tableau contient 4, 7.

La seconde méthode annexe se nomme int[] merge(int val, int[] tab) et effectue l'opération inverse : elle renvoie un nouveau tableau dont le premier élément est val suivi d'une copie des éléments de tab. Vérifiez que votre méthode est correcte en affichant le résultat de merge(1, t1).

Nous pouvons maintenant mettre en œuvre la fusion. Pour cela, vous allez écrire une nouvelle méthode nommée merge, prenant en argument deux tableaux t1 et t2 triés et renvoyant la fusion de ces deux tableaux. Le fait qu'il y ait deux méthodes merge ne pose pas de problème, car les arguments des deux méthodes sont différents, ce qui permet à Java de savoir quelle méthode on souhaite appeler en fonction des paramètres.

Nous mettons en œuvre merge de façon récursive :

Si t1 a une taille égale à zéro, alors merge doit renvoyer t2
Si t2 a une taille égale à zéro, alors merge doit renvoyer t1
Si t1[0] est plus petit que ou égal à t2[0], alors merge doit renvoyer le tableau construit à partir de t1[0] et du résultat de la fusion de la partie droite de t1 avec le tableau t2. La partie droite de t1 s'obtient en appelant la méthode right et l'ajout à gauche de t1[0] s'obtient en appelant la seconde méthode merge que vous avez défini à la question précédente.
Dans le cas inverse, il suffit d'appeler merge en inversant les rôles de t1 et t2.

Testez merge en affichant le résultat de la fusion de t1 et t2 dans la méthode main.

MergeSort.java

Quelle est la complexité de la fonction merge prenant en entrée deux tableaux ?

Tout d'abord, on note que les fonctions right et int[] merge(int val, int[] tab) sont linéaires en la taille du tableau en entrée, car elles demandent de recopier le tableau donné en entrée. Ensuite, nous allons exprimer la complexité de merge en fonction de la somme des tailles des deux tableaux en entrée que nous appelons n.
Les deux cas les plus couteux sont les deux derniers. On note que le dernier cas se produit au maximum n fois. L'avant-dernier cas nous donne la relation de récurrence suivante:

C(n) = n + C(n-1)

Où le n vient de right et int[] merge(int val, int[] tab). On appelle ensuite merge avec un élément en moins dans un des tableaux. À partir de là, nous avons:

C(n) = \sum_{i=1}^n i = \frac{n(n+1)}{2} = \mathcal{O}(n^2)

La complexité finale de merge est donc quadratique.

(Optionnel) Cette complexité vous semble-t-elle optimale ? Pourriez-vous proposer un autre algorithme ? Quelle est sa complexité ?

Le problème de l'algorithme présenté plus haut est qu'il recopie beaucoup de fois des tableaux. Au lieu d'avoir un algorithme récursif, nous pourrions avoir un algorithme itératif fonctionnant de la manière suivante :

Création du tableau final de taille égale à la somme des deux tailles.
Pour chacune des deux tableaux t0 et t1, nous conservons indice i0 et i1 nous indiquant notre position dans chaque tableau. Ces indices sont initialisés à 0 et seront incrémenté de 1 à chaque fois qu'un élément sera ajouté au tableau final.
Tant que les deux indices ne sont pas égaux à la taille de leur tableau respectif, prendre la valeur la plus petite entre t0[i0] et t1[i1] et la rajouter au tableau final. Incrémenter la valeur de l'indice ayant amené l'ajout.

On peut écrire un algorithme de complexité linéaire en ayant pour chaque tableau un pointeur sur la position actuelle que l'on avance au moment opportun.

MergeSort2.java

le partitionnement

Dans cette partie, nous nous occupons de partitionner un tableau.

Commencez par supprimer les tests actuels de la méthode main (les définitions des t1 et t2 incluses). À la place, allouez un tableau d'entiers nommé tab initialisé à 4, 7, 3, 9, 1, 2, 5.

Écrivez une méthode int[] extract(int[] tab, int start, int end) qui extrait de tab le sous-tableau commençant à l'indice start inclus et finissant à l'indice end non inclus. Testez votre méthode extract en affichant le résultat de l'extraction de la moitié gauche de tab dans la méthode main. Vous devriez obtenir le tableau 4, 7, 3.

le tri fusion

Nous pouvons enfin mettre en œuvre l'algorithme du tri-fusion.

Écrivez une méthode int[] mergeSort(int[] tab) mettant en œuvre l'algorithme de tri fusion pour renvoyer un tableau contenant les éléments de tab triés.

Pour vous guider, nous vous proposons d'utiliser un algorithme récursif :

Si tab a une taille inférieure ou égale à 1, alors le tableau est déjà trié et il suffit de le renvoyer.
Sinon, il faut appeler mergeSort sur la partie gauche de tab, puis mergeSort sur la partie droite de tab et enfin utiliser merge pour fusionner les résultats des deux appels à mergeSort.

MergeSort.java

MergeSort2.java

Quelle est la complexité de mergeSort ?
On rappelle que :

\sum_{n = 1}^{\infty} (\frac{1}{n^{2}}) \leq 2

Nous partons du principe que la complexité de merge est quadratique (c.f. plus haut). Dans ce cas, à chaque appel à mergeSort, nous exécutons au pire deux nouveaux mergeSort avec des tableaux deux fois plus petits et une fusion. La complexité de extract étant linéaire, on peut l'ignorer au profit de merge qui est quadratique. On a donc la relation de récurrence :

C (n) = n^{2} + 2 C (\frac{n}{2}) = n^{2} + 2 * (\frac{n}{2})^{2} + 4 C (\frac{n}{4}) = n^{2} (1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + . . .) \leq 2 * n^{2}

La complexité est donc quadratique.
En réalité, la complexité avec un merge efficace est

\mathcal{O}(nlog(n))

, ce qui est la complexité optimale pour un algorithme de tri ! En effet, la relation de récurrence devient :

C (n) = n + 2 C (\frac{n}{2}) = n + 2 * \frac{n}{2} + 4 C (\frac{n}{4}) = n * (1 + 1 + 1 + 1 + . . .) = O (n * l o g (n))

Le log vient du fait que l'on divise n par deux jusqu'à obtenir un nombre inférieur à 1.

Félicitations ! Vous venez de mettre œuvre votre premier algorithme complexe en Java !