- Exercice 1 : obligatoire (facile, ∼30mn)
- Exercice 2 : obligatoire (facile, ∼30mn)
- Exercice 3 : obligatoire (facile, ∼20mn)
- Exercice 4 : obligatoire (ninja, ∼1h)
- Exercice 5 : entraînement (moyen, ∼20mn)
- Exercice 6 : entraînement (difficile)
Dans cet exercice, nous concevons un petit programme de navigation permettant de se déplacer en voiture. Ce programme vous permet de calculer le chemin optimal permettant d'aller d'une ville à une autre en utilisant l'algorithme du plus court chemin de Dijkstra. Pour cela, vous avez besoin de manipuler des graphes pondérés. Un graphe est une structure mathématique dans laquelle des nœuds sont reliés par des arcs possédant un poids. Dans notre cas, les nœuds sont des villes, les arcs symbolisent les routes et le poids d'un arc donne la distance à parcourir sur la route.
Les villes et les routes (∼30mn – facile – obligatoire)
Dans cette première partie, nous construisons quelques villes et les relions entre elles. Une ville possède un nom et des coordonnées GPS. Elle est reliée à d'autres villes par des routes.
- un champ name donnant le nom de la ville,
- des champs latitude et longitude de type double donnant les coordonnées GPS de la ville.
On souhaite maintenant calculer la distance entre deux villes en kilomètres. La formule permettant de calculer la distance entre deux points d'une sphère dont les coordonnées sont données en radian est :
Dans cette formule R est le rayon de la terre (6378km). Cette formule utilise directement les méthodes Java permettant d'effectuer des opérations de trigonométrie.
Écrivez une méthode d'instance double distanceTo(Location to) renvoyant la distance en kilomètres entre le receveur de l'appel (c'est-à-dire this) et to.
Pour tester votre méthode, créez une variable locale nommée paris dans votre main pour référencer la ville de Paris se trouvant aux coordonnées (48.85661400000001, 2.3522219000000177). Ensuite, vérifier que la distance à vol d'oiseau entre Evry et Paris est bien de 26 kilomètres environ.
En plus d'Evry et Paris, vous pouvez maintenant ajouter quelques villes à votre main en copiant-collant le code ci-dessous :
Nous pouvons maintenant associer des voisins aux villes. Si une ville B est voisine de A, c'est qu'il existe une route directe pour aller de A à B. Comme il existe des sens uniques, ce n'est pas parce que B est voisine de A que A est forcément voisine de B.
De façon à modéliser les routes, commencez par ajouter à la classe Location un champ nommé neighbors référençant un tableau de Location. Ensuite, ajoutez une méthode d'instance void setNeighbors(Location... neighbors) à votre classe Location. Les trois petits points permettent de spécifier que le nombre de paramètres n'est pas à priori connu, mais que ces paramètres sont tous du type Location. Du côté de l'appelant, on peut alors spécifier un nombre quelconque de voisins, comme avec l'expression :
Du côté de l'appelé, neighbors est simplement un tableau dont les éléments sont les arguments : avec notre exemple, neighbors est un tableau dont les éléments sont des références vers Limoges, Tours et Orléans. Vous pouvez donc directement assigner neighbors à this.neighbors dans setNeighbors.
Complétez votre méthode main avec le code suivant permettant de créer quelques routes :
La ville à distance minimale (∼30mn – moyen – obligatoire)
À haut niveau, pour calculer le plus court chemin d'une ville A à une ville B, l'algorithme parcourt le graphe des villes en partant de A et propage la distance minimale pour atteindre chaque ville de voisin en voisin. À chaque étape de l'algorithme, il faut être capable de trouver la ville la plus proche de l'origine. Pour cela, nous concevons une structure de données annexe permettant de trouver la ville la plus proche de l'origine dans cet exercice.
Commencez par ajouter un champ privé distance de type double à la classe Location et une méthode double getDistance() permettant de consulter cette distance. À terme, ce champ nous servira à stocker les distances minimales pour atteindre les villes. Pour le moment, initialisez ce champ à une valeur aléatoire comprise entre 0 et 100 dans le constructeur de Location en utilisant Math.random() qui renvoie une valeur aléatoire comprise entre 0 et 1.
Nous commençons maintenant à mettre en œuvre la classe LocationSet permettant de trouver la ville avec le champ distance minimal. Comme le nombre de villes stockées dans le LocationSet n'est pas connu à priori, nous utilisons un tableau extensible (voir CI3). Ajoutez une classe nommée LocationSet dans le package tsp.shortestpath contenant deux champs privés :
- locations : un tableau de Location,
- nbLocations : un entier indiquant combien de Location sont stockées dans le tableau.
Dans le constructeur de LocationSet, initialisez nbLocations à 0 et locations avec un tableau de 100 cases.
Allouez une instance de LocationSet que vous stockerez dans une variable nommée test à la fin de la méthode main.
Ajoutez maintenant une méthode void add(Location location) à la classe LocationSet permettant d'ajouter un nouvel élément au tableau. Les étudiants expérimentés peuvent gérer le cas où il faut étendre le tableau (dans ce cas, pré-initialisez le tableau avec 4 cases au lieu de 100), les autres peuvent considérer que le tableau a une taille suffisante pour accueillir tous les nœuds et ainsi éviter de gérer le cas où il faut étendre le tableau.
Dans la méthode main, ajoutez les villes de Paris, Evry et Orléans au LocationSet référencé par test.
Ajoutez enfin une méthode d'instance Location removeMin() à la classe LocationSet. Cette méthode doit trouver la ville avec le plus petit champ distance du LocationSet, retirer cette ville du LocationSet, et enfin renvoyer cette ville. Vérifiez que votre code est correct en ajoutant, à la fin du main, le code suivant qui retire les villes en suivant l'ordre croissant des distances :
En détail :
- Location removeMin() doit renvoyer null si nbLocations est égal à 0,
- sinon, elle doit :
- trouver l'indice min du nœud avec la plus petite distance parmi les nœuds enregistrés dans l'ensemble,
- supprimer ce nœud (pour supprimer l'élément se trouvant dans la case min du tableau, il suffit de copier l'élément locations[nbLocations-1] dans la case min avant d'ôter 1 à nbLocations),
- et enfin renvoyer ce nœud.
Avant de passer à la suite, nous supprimons les tests que nous avons conçus à cette question :
- supprimez du constructeur de Location l'initialisation de distance a une valeur aléatoire (l'initialisation correcte de ce champ sera effectué dans l'exercice suivant),
- supprimez du main l'allocation de test, les ajouts de villes à test et enfin le code qui vérifie que removeMin() est correcte.
Principe de l'algorithme du plus court chemin (∼20mn – facile – obligatoire)
Cet exercice a pour but de vous présenter l'algorithme du plus court chemin et de préparer l'exercice suivant dans lequel vous mettez en œuvre cet algorithme.
Pour calculer le plus court chemin d'un nœud A à un nœud B, le principe est de calculer de proche en proche, en suivant les voisins, les distances minimales permettant d'atteindre chaque nœud. Pour cela, on stocke la distance minimale pour aller de A à chaque nœud déjà rencontré dans le champ distance de Location (voir Exercice 2).
À haut niveau, l'algorithme choisit, à chaque étape, le nœud N ayant le plus petit champ distance. La figure suivante illustre l'algorithme avec le calcul du plus court chemin pour aller de A à E dans le graphe A, B, C, D et E (les nombres sur les arcs sont les distances).
| A | B | C | D | E | ||
| Étape 0 | 0 (null) | ∞ (?) | ∞ (?) | ∞ (?) | ∞ (?) | Choisit A, marque A visité et propage la distance aux voisins (0+1 pour B qui vient de A) |
| Étape 1 | - (null) | 1 (A) | ∞ (?) | ∞ (?) | ∞ (?) | Choisit B, marque B visité et propage la distance aux voisins (1+2 pour C et 1+3 pour D qui viennent de B) |
| Étape 2 | - (null) | - (A) | 3 (B) | 4 (B) | ∞ (?) | Choisit C, marque C visité et propage la distance aux voisins (3+6 pour E qui vient de C) |
| Étape 3 | - (null) | - (A) | - (B) | 4 (B) | 9 (C) | Choisit D, marque D visité et propage la distance aux voisins (4+1 plus petit que 9 ⇒ met à jour E avec 5, et E vient maintenant de D) |
| Étape 4 | - (null) | - (A) | - (B) | - (B) | 5 (D) | Choisit E, destination atteinte, le chemin le plus court est à une distance de 5, et le chemin inverse le plus court est E -> D -> B -> A |
- non atteint : le nœud n'a pas encore été atteint par l'algorithme. Ce sont les nœuds à distance infini (par exemple C, D et E à l'étape 1).
- atteint : le nœud a été atteint et on le considère comme potentiel prochain départ pour l'étape suivante. Par exemple, à l'étape 2, C et D sont atteints.
- visité : le nœud est atteint et sa distance a été propagée à ses voisins à une des étapes de l'algorithme. C'est, par exemple, le cas des nœuds A et B à l'étape 2 de l'algorithme.
- si V est toujours non atteint, l'algorithme le marque atteint,
- dans tous les cas, l'algorithme calcule la distance pour atteindre V en passant par N. Si cette nouvelle distance est plus petite qu'une distance précédemment trouvée (par exemple, c'est le cas à l'étape 3 de l'algorithme pour le voisin E de D), l'algorithme met à jour la distance du voisin. Dans ce cas, l'algorithme mémorise aussi dans V que le plus court chemin vient de N dans un champ from que nous ajoutons à Location. Par exemple, à l'étape 3, comme atteindre E en venant de D est plus court qu'en venant de C, on note que la route la plus courte pour atteindre E provient de D et non de C (voir le résultat à étape 4).
- Si le champ distance d'un nœud vaut l'infini, c'est que le nœud est encore non atteint.
- Si son champ distance n'est pas égal à l'infini, c'est qu'il est soit atteint, soit visité. On considère qu'un nœud est atteint s'il est dans le LocationSet et qu'il est visité lorsqu'il n'y est plus.
Pour calculer le plus court chemin d'une origine à une destination, nous avons déjà besoin d'ajouter un champ from à la classe Location. Ce champ indique le prédécesseur du nœud en suivant le chemin le plus court. Il n'est pas nécessaire d'initialiser ce champ dans le constructeur de Location car il sera initialisé lorsque son nœud sera marqué atteint. En revanche, on vous demande à cette question d'ajouter ce champ à Location.
Comme expliqué précédemment, les nœuds doivent être initialement à l'état non atteint, c'est-à-dire que leur champ distance doit être égal à l'infini. Modifiez le constructeur de Location de façon à initialiser le champ distance à l'infini (Double.POSITIVE_INFINITY en Java).
Ajouter enfin une méthode void findPathTo(Location to) ne faisant rien à la classe Location. Pour le moment, cette méthode ne fait rien, mais à terme, cette méthode va afficher le plus court chemin pour aller de this à to. Dans la méthode main, appelez evry.findPathTo(bilbao) qui va nous servir à tester notre code dans la suite de l'exercice.
Mise en œuvre du plus court chemin (∼1h – ninja – obligatoire)
- Initialisation du calcul. Cette étape préliminaire doit, comme indiqué dans la figure au-dessus, sélectionner le nœud d'origine après avoir initialisé son champ distance à 0.
- Mise en place de la boucle permettant de passer d'une étape à la suivante. Comme indiqué dans la figure au-dessus, cette boucle doit sélectionner la ville atteinte ayant la distance la plus courte à l'origine.
- Réalisation d'une étape du calcul. Comme expliqué précédemment, une étape consiste en marquer le nœud sélectionné comme visité et en propager la distance à ses voisins.
- Affichage du chemin. Cet affichage doit partir de to et remonter le graphe en suivant les champs from jusqu'à l'origine.
Après un calcul de plus court chemin, l'affichage que devrait produire votre programme est le suivant :
Dans void findPathTo(Location to), utilisez l'algorithme de Dijkstra pour calculer et afficher le plus court chemin pour aller de this à to. Après avoir testé votre algorithme pour aller de Evry à Bilbao, vérifiez qu'il n'existe pas de chemin partant de Bilbao et allant à Evry.
Pour mettre en œuvre l'algorithme, nous vous proposons de concevoir une méthode d'instance intermédiaire dans la classe Location. Cette méthode, nommée void proceedNode(LocationSet set), s'occupe de réaliser une étape de l'algorithme (voir la figure ci-dessus), en considérant que this est le nœud courant. Typiquement, le this à la fin de l'étape 2 est le nœud C. Cette méthode propage la distance aux voisins de this, et ajoute les voisins de this à set (variable de type LocationSet) lorsqu'ils sont non atteints.
Une fois cette méthode mise en œuvre, vous pouvez chercher le plus court chemin de this à to dans findPathTo en enchaînant, dans une boucle, des appels à removeMin (qui vous permet de trouver la ville cur qui est à la distance minimale de l'origine) et des appels à proceedNode (qui s'occupe de propager la distance aux voisins de cur).
Cette série de questions vous guide pas à pas pour réaliser les méthodes findPathTo et proceedNode.
Afin d'initialiser l'algorithme, commencez par allouer un nouveau LocationSet dans findPathTo que vous stockerez dans une variable nommée set. Ensuite, positionnez le champ distance de this à 0. Enfin, définissez une variable de type Location nommée cur. Cette variable sert à référencer le nœud utilisé à l'étape courante. À l'initialisation (voir figure), le nœud courant est le nœud d'origine. Il faut donc initialiser cur à this.
Afin de mettre en œuvre la boucle permettant de passer d'une étape à la suivante, il faut savoir que :
- l'algorithme se termine lorsque (i) cur vaut null, ce qui signifie qu'aucun chemin n'a été trouvé ou (ii) cur vaut to, ce qui signifie que l'algorithme a réussi à trouver le chemin minimum permettant d'atteindre to,
- on passe d'une étape à la suivante en retirant le nœud ayant la distance minimum de set en appelant removeMin() et en le sélectionnant comme nœud courant. Comme le nœud est retiré de set, il passe à l'état visité sans avoir besoin d'opération supplémentaire.
À cette étape, écrivez la boucle permettant de passer d'une étape à la suivante. Pour le moment, laissez le corps de cette boucle vide. Nous nous occupons de compléter ce code à la question suivante.
Afin de réaliser une étape de l'algorithme, ajoutez la méthode d'instance void proceedNode(LocationSet set) à la classe Location. Ensuite, dans la boucle que vous venez de mettre en œuvre à la question précédente, ajoutez un appel à cur.proceedNode(set) afin de réaliser une étape de l'algorithme. Dans proceedNode(), vous devez propager la distance aux voisins.
Techniquement, vous devez donc parcourir les voisins de this, et pour chaque voisin n, vous devez :
- si n a encore une distance infinie, ça signifie que le nœud est encore non atteint. Il faut l'ajouter à set pour le marquer atteint. En revanche, il n'est pas nécessaire de modifier son champ distance qui sera de toute façon modifié par la suite.
- dans tous les cas, il faut calculer la distance permettant d'atteindre n en passant par this en ajoutant this.distanceTo(n) à this.distance,
- si cette nouvelle distance est plus petite que la distance actuelle enregistrée dans n, il faut (i) mettre à jour n.distance avec la nouvelle distance minimale trouvée, et (ii) affecter this à n.from afin de mémoriser que le chemin le plus court provient de this.
Votre algorithme calcule maintenant le plus court chemin, on vous demande donc de l'afficher à la fin de Location.findPathTo.
Après la boucle de calcul du plus court chemin, vous avez deux choix :
- si cur vaut null, c'est que l'algorithme n'a pas réussi à atteindre to. Il vous suffit d'afficher un message adéquat,
- sinon, c'est que l'algorithme a trouvé un chemin. Il vous suffit, dans une boucle, de remonter l'arbre des from en partant de to afin de remonter à l'origine (this). À chaque itération de la boucle, pensez à afficher la ville que vous avez trouvé.
- Combien d'itérations fera la boucle dans la fonction proceedNode (voir l'aide plus haut) en tout et au maximum ?
- Combien de fois au maximum la fonction removeMin est-elle appelée ?
Parcours en profondeur (∼20mn – moyen – entraînement)
Notre algorithme ne permet que d'effectuer un unique calcul de plus court chemin. En effet, une fois que le champ distance a été affecté à une valeur pendant le calcul du plus court chemin, le nœud est définitivement considéré comme atteint ou visité, y compris lors des parcours suivants. Dans cet exercice, nous ajoutons donc une méthode reinit() permettant de remettre les nœuds à l'état non atteint après un calcul du plus court chemin.
Cette méthode reinit() parcourt le graphe en profondeur, c'est-à-dire qu'elle explore le graphe des nœuds atteignables à partir de l'origine en commençant par aller le plus loin possible dans le graphe en suivant les voisins.
Pour commencer, ajoutez une méthode d'instance vide void reinit() à la classe Location et appelez-la à la fin de findPathTo.
Mettez en œuvre la méthode reinit() de la classe Location permettant de réinitialiser les champs distance des villes.
Techniquement, reinit() doit réinitialiser le champs distance de this à Double.POSITIVE_INFINITY puis appeler reinit() sur les voisins de this.
Les graphes que nous considérons dans cet exercice sont cycliques : de Paris, on peut aller au Mans, puis à Orléans avant de revenir à Paris.
Pour éviter d'appeler reinit() indéfiniment lorsqu'on parcourt un cycle, il faut noter par quels nœuds nous sommes déjà passés. Pour cela, il suffit d'utiliser directement la variable distance : lorsque cette variable est égale à Double.POSITIVE_INFINITY, c'est que le nœud a déjà été atteint. Dans ce cas, il ne faut donc pas appeler reinit sur les voisins.
Dans la méthode main, après avoir calculé le plus court chemin pour aller d'Evry à Bilbao, calculez le plus court chemin pour aller d'Angers à Toulouse.
Tas Binaire (entraînement)
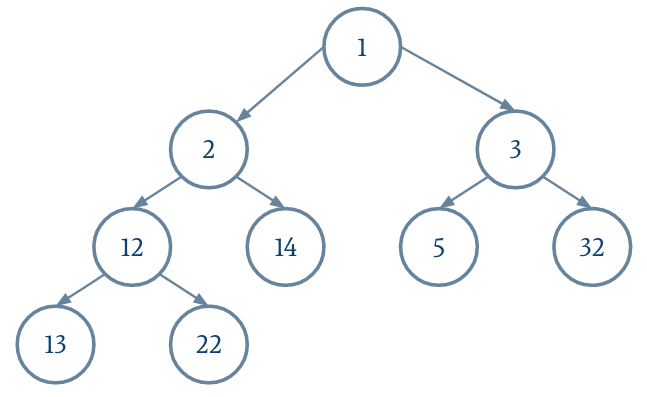
- Un arbre binaire (c.f. CI précédent) complet. La complétude signifie que tous les niveaux sauf le dernier sont pleins. Pour le dernier niveau, il est rempli de gauche à droite.
- Un tas, c'est-à-dire que le poids de chaque nœud est inférieur ou égal à celui de chacun de ses fils.
m
Pour cet exercice, nous allons utiliser un tableau extensible de Location. Initialiser ce tableau avec une taille initiale de 100 et un indice maximum de 0.
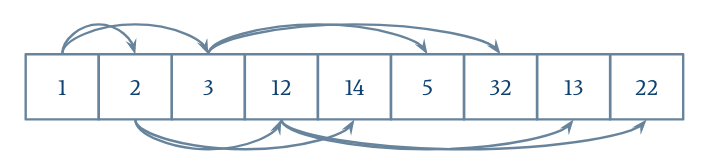
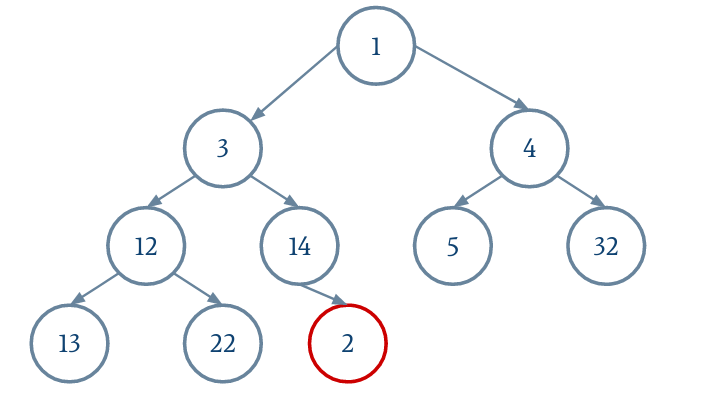
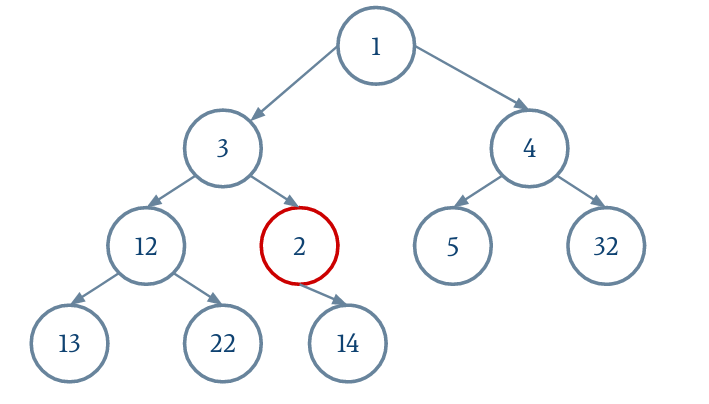
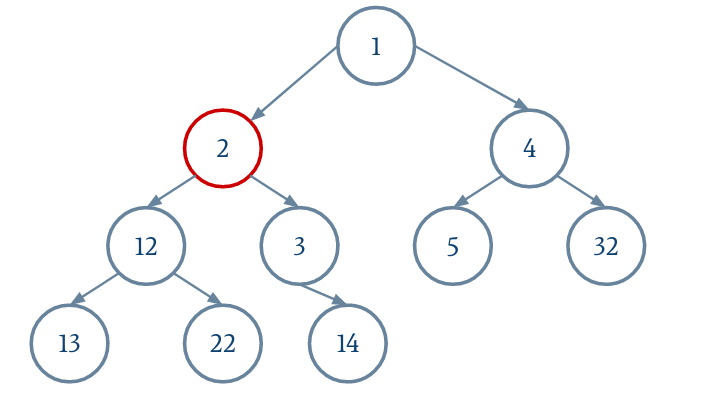
Le parent d'un nœud i est donné par (i - 1) / 2.
Les IDEs permettent en général de faire l'opération d'extraction de méthode de manière automatique. Pour cela, sélectionnez le code que vous voulez extraire, faites click droit dessus, Refactor > Extract Method... (ou quelque chose de similaire suivant votre IDE).
Comme la méthode percolateUp est une méthode interne, elle ne doit pas être accédée depuis l'extérieur. Faites-en sorte que ce soit le cas.
Vous aurez surement envie de créer également une fonction auxiliaire swap pour échanger deux indices.
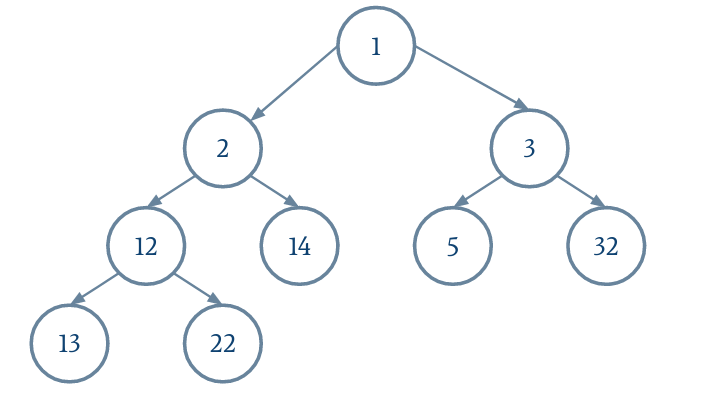
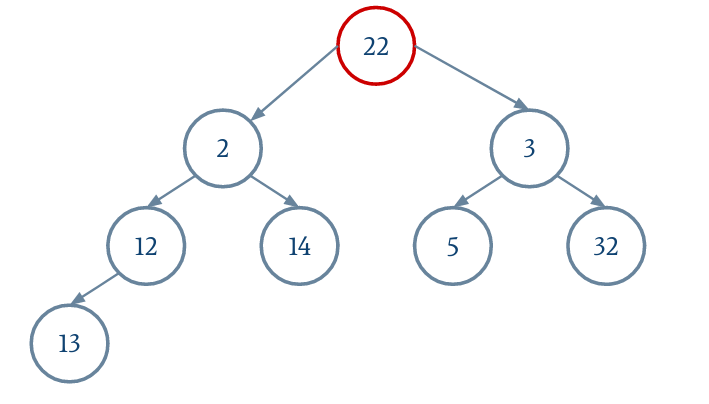
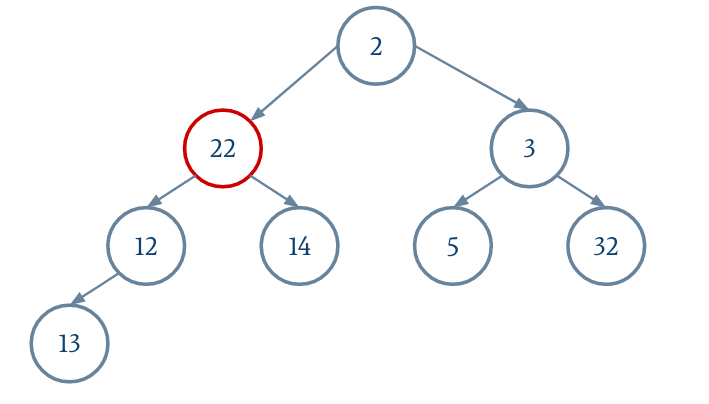
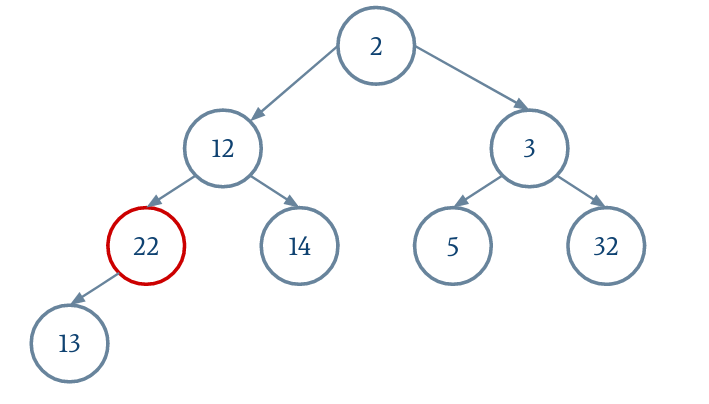
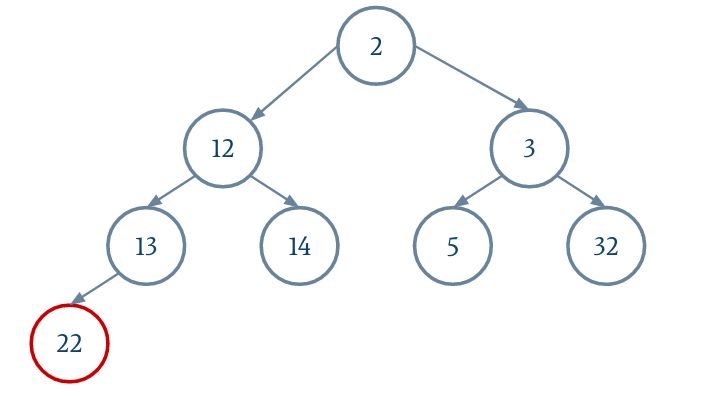
On n'oubliera pas de réduire la taille du tableau extensible.
Lors de la descente, on remplace le nœud actuel par le plus petit des fils si ce dernier est plus petit que le nœud actuel.
Vous venez de créer le tri par tas !
Il faut bien penser à mettre à jour correctement les Locations.
C'est là la beauté de l'encapsulation ! Nous avons exposé une interface simple (findPathTo) et nous avons pu modifier ce qui se passe dans les coulisses sans conséquences négatives sur les utilisateurs.
Il est encore possible d'améliorer les performances de l'algorithme de Dijkstra en utilisant des Tas de Fibonacci (décidément, il est partout). Les étudiants les plus curieux pourront se lancer dans l'implémentation. Ils obtiendront alors une complexité en .

