CI9 : Une intelligence artificielle pour Pacman
L'objectif de cet exercice d'une part de revoir les notions vues dans ce cours, mais aussi de vous introduire à la programmation d'intelligences artificielles simples dans un jeu vidéo.
Ce TP est long si vous voulez le compléter en entier, de quoi vous occuper à Noël pendant que vous digérez le repas !
Durée des exercices obligatoires : 2h30mn en présentiel TODO- Exercice 1 : obligatoire (moyen, ∼1h30min)
- Exercice 2 : obligatoire (moyen, ∼30mn)
- Exercice 3 : obligatoire (moyen, ∼45mn)
- Exercice 4 : obligatoire (moyen, ∼1h)
- Exercice 5 : entraînement (moyen, ∼30mn)
- Exercice 6 : entraînement (moyen, ∼20mn)
- Exercice 7 : entraînement (difficile, ∼60mn)
Dans cet exercice, nous allons revenir sur un classique du jeu vidéo : Pacman. Nous verrons comment modéliser un environnement afin qu'il soit exploitable par des algorithmes spécialisés. À la fin de ce TP, vous aurez un Pacman intelligent capable de se diriger seul dans son univers et, qui sait, peut-être prendre le contrôle du nôtre !
Pac-Man est un jeu vidéo créé par Tōru Iwatani en 1980. On y interprète Pac-Man, un monstre jaune bloqué à l'intérieur d'un labyrinthe et qui doit manger toutes les pac-gommes de son monde. Cependant, il est poursuivi par des fantômes qui ne doivent pas l'attraper. Le but du jeu est de manger toutes les pac-gommes le plus vite possible.
Modéliser un univers (∼1h30min – moyen – obligatoire)
Une "situation" est appelée en informatique un état du système. Plus le système est compliqué, plus la représentation devra l'être aussi. Toutefois, il revient au programmeur de choisir ce qui fait partie de l'état. Dans le cas le plus large, il faudrait toujours décrire la position exacte de chaque particule dans l'univers. Bien sûr, cela est impossible et notre IA n'a pas besoin de tout savoir pour travailler.
Par exemple, dans le cas du jeu d'échec, un état correspondra à l'emplacement de toutes les pièces, le joueur qui doit jouer, ainsi qu'une information sur les roques. Pour un jeu plus complexe comme Minecraft, il faudra potentiellement donner plus informations : l'emplacement de tous les blocs visibles, la position des joueurs et PNJ, les objets dans l'inventaire, le nombre de points de vie, l'heure de la journée, ... Cependant, cela dépendra de ce que fait vraiment votre IA : Une IA qui guide d'un point A à un point B n'a potentiellement besoin que de la position du joueur et d'une carte du terrain.
Dans ce TP, nous allons écrire une intelligence artificielle pour Pacman. Le but de Pacman est de manger toute la nourriture de son univers. Pour cela, il va avoir besoin de connaitre sa position ainsi que la position de toutes les nourritures.
- Un constructeur public Position(int row, int col)
- Des getters getRow et getCol pour accéder aux attributs.
- Une méthode pour tester l'égalité de deux positions.
- Une méthode pour obtenir le hash d'une position. On pourra pour cela utiliser la méthode Integer.hashcode et faire l'opération hash(x) * 31 + hash(y) (on ne veut pas une opération symétrique).
- Une méthode qui permettra de transformer une position en String.
- Une méthode dist pour calculer la distance entre deux positions. La distance que nous utiliserons sera la distance de Manhattan, donnée par :
- public boolean equals(Object o)
- public int hashCode()
- public String toString()
- % représente un mur.
- . représente une nourriture.
- Un espace représente une case vide.
Écrivez un nouveau constructeur prenant en entrée une chaîne de caractères et initialisant correctement les attributs. Pour cela, nous aurons besoin des méthodes suivantes déjà implémentées en Java permettant de manipuler les String :
- String strip(): Permet de retirer les espaces et retours à lignes pouvant être présents au début et à la fin d'une String. Cela est utile, car souvent, quand nous avons une String sur plusieurs lignes, il est plus lisible de rajouter des espaces.
- String[] split(String c): Permet de séparer une String en sous-chaînes de caractères en utilisant le caractère c (donné sous forme d'un String) comme délimiteur. C'est par exemple utile pour séparer les lignes en utilisant le caractère de retour à la ligne \n.
- char charAt(int index): Obtient le caractère à un index donné.
- int length(): Donne la longueur de la chaîne de caractères.
Vous allez devoir utiliser strip une première fois pour retirer les sauts de lignes potentiels au début et à la fin de la String. Ensuite, vous devez faire un split("\n") pour obtenir un tableau de String ou chaque ligne est séparée. Il faudra alors itérer sur cette ligne et itérer sur chaque caractère de cette ligne pour utiliser charAt(int index). Le caractère à la ligne i et à l'index j sera dans this.board[i][j]. On prendra garde de traiter le cas avec Pacman à part.
Pour initialiser le tableau, vous pourrez utiliser le nombre de lignes et la longueur de la première ligne (il y a toujours au moins une ligne).
Pour tester votre code, vous pouvez créer une méthode main dans la classe PacmanState.
Pour la représentation textuelle, vous devez redéfinir la méthode toString. Vous pouvez soit utiliser la concaténation de String avec + ou la classe StringBuilder donnée par Java qui est plus rapide.
N'oubliez pas d'afficher Pacman !
Testez votre code dans le main.
Nous rappelons que ArrayList est une classe générique définie par Java qui correspond aux tableaux extensibles. Pour rajouter un élément à cette liste, vous pouvez utiliser la méthode add. Pour accéder à un élément, vous pouvez utiliser la méthode get (et non les crochets !).
La liste des positions où Pacman peut se rendre dans l'état actuel constitue les actions disponibles à Pacman. En règle générale, une IA doit choisir une action étant donné un état du système. Par exemple, les actions aux échecs sont la liste des coups légaux. Pour une IA qui génère du texte comme ChatGPT, l'état est la liste des mots précédents de la conversation et les actions sont la liste des mots de son vocabulaire.
Écrivez une méthode List<Position> findPossibleMoves(Position position) qui nous donne toutes les positions où un Pacman à la position position peut se déplacer légalement. Le résultat sera une ArrayList en interne.
Comme cette méthode sera souvent utilisée avec la position de Pacman en argument, on définira une méthode List<Position> findPossibleMoves() qui retournera le résultat de findPossibleMoves appelé sur pacmanPosition.
Vérifiez dans le main que pour notre exemple, il n'y a qu'une seule action légale.
- boolean isInside(Position position) : Retourne si une position est dans le board ou non.
- boolean isLegalMove(Position position) : Retourne si une position donnée est un déplacement légal (ou de mur et dans le board).
- void processPositionLegalMoves(Position position, ArrayList<Position> res) : Ajoute position à res si la position est un déplacement légal.
Quand nous simulons les successeurs d'un état, il est très important de ne pas modifier l'état actuel ! Comme nous le verrons par la suite, nous aurons besoin d'y revenir. Pour cela, nous allons devoir copier notre tableau interne. Implémentez une méthode char[][] copyBoard() qui copie le tableau.
Attention de ne pas copier des références !
Pour la copie, il faut recréer un nouveau tableau avec la bonne taille et faire une double boucle.
Une fois cette copie effectuée, implémentez une méthode PacmanState move(Position to) qui, étant donné une position, simule l'état suivant sans modifier l'état actuel. On considèrera que quand Pacman quitte une position, il laisse derrière lui une case vide. On rappelle qu'il faut créer un nouvel état et ne pas modifier l'état actuel.
Pour tester votre code, faites bouger Pacman en (3, 7) et vérifiez qu'il a maintenant deux actions légales.
Écrivez une méthode boolean isFinalState() déterminant si nous avons atteint un état final.
Tester que notre exemple n'est pas un état final et que, si l'on enlève la seule nourriture, il devient final.
Vous pouvez utiliser la méthode findFoods écrite plus haut.
On écrira également une fonction getScore permettant d'obtenir le score d'un état.
Testez que l'état initial a bien un score de 0 et l'état après un déplacement un score de 1.
N'oubliez pas de modifier move !
- Arrays.deepEquals : Permet de vérifier l'égalité de tableaux imbriqués.
- Arrays.deepHashCode : Permet de calculer le hash de tableaux imbriqués.
Nous rappelons qu'il faut redéfinir les méthodes boolean equals(Object o) et int hashCode().
Visualisez un univers (∼30min – moyen – obligatoire)
Cette classe prend en argument la hauteur (premier indice du tableau) et la largeur (deuxième indice du tableau) du monde de Pacman. On peut afficher un état donné en utilisant la fonction void update(PacmanState pacman).
Pour notre Pacman, notre boucle va s'exécuter jusqu'à ce que nous ayons atteint un état final. À chaque étape de la boucle, notre simulateur :
- Demande à notre IA de choisir une action pour l'état actuel.
- Remplace l'état actuel par l'état suivant l'action.
- Met à jour l'affichage. Pour cela, il faut appeler la fonction update(state) de PacmanVisualizer.
- Patiente un certain laps de temps (pour pouvoir humainement voir ce qui se passe). Pour cela, vous pouvez utiliser la fonction System.currentTimeMillis() qui donne le temps actuel en millisecondes et une boucle while vide.
Implémentez ensuite la boucle de jeu dans une méthode void gameLoop() et affichez le score une fois la partie finie.
Pour obtenir un index aléatoire dans une ArrayList, on peut faire (int)(Math.random() * positions.size()).
Gérer les déplacements (∼45min – moyen – obligatoire)
Dans tout cet exercice, nous considérons qu'il n'y a qu'une seule nourriture à trouver et que nous voulons trouver un chemin pour y aller.
Les algorithmes que nous allons voir sont très semblables à ceux utilisés pour les graphes et que nous avons vu dans les CIs précédents. La raison est simple : nous pourrions représenter notre board avec un graphe où les nœuds sont les positions et les connexions les actions légales.
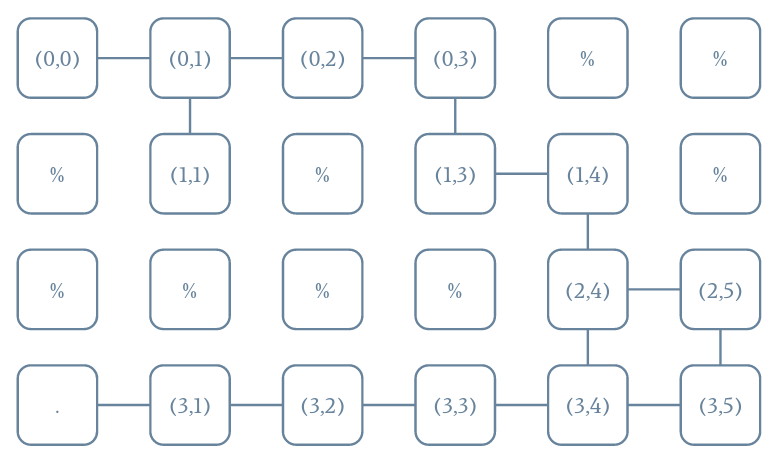
Testez votre code avec le Pacman aléatoire et remarquez que toutes les positions visitées deviennent vertes.
Quelle structure de données vous semble la plus adaptée pour cet algorithme, c'est-à-dire à accéder aux nouveaux éléments en premier ? Vous pouvez consulter une liste de structures de données et d'algorithmes ici.
Les différents parcours utilisent soit Stack (pile), soit Queue (une file, à travers LinkedList), soit PriorityQueue (une file de priorité).
Il est important que PacmanDFSTeleport se souvienne des positions déjà visitées. Il faudra pour cela utiliser la structure de données idoine et l'initialiser dans le constructeur.
Visualizer votre recherche en créant un nouveau Pacman.
Vous allez devoir utiliser un HashSet. Il vous faut initialiser deux champs dans le constructeur : HashSet<Position> visited et Stack<Position> toVisit. Voici le pseudo code de l'algorithme dans chooseAction:
Quelle structure de données vous semble la plus adaptée pour cet algorithme ?
Les différents parcours utilisent soit Stack (pile), soit Queue (une file, à travers LinkedList), soit PriorityQueue (une file de priorité).
Visualizer votre recherche.
Commencez par créer une classe PacmanAStarTeleport qui met en œuvre Pacman.
Dans cet exercice, nous considèrerons que la priorité d'une position dans l'exploration est donnée par sa distance de Manhattan avec l'état final + le coût déjà payé pour atteindre la position actuelle (c'est-à-dire le score implémenté plus haut). Comme la priorité dépend de la position de la nourriture, nous devons transmettre l'état initial au constructeur.
Pour nous rappeler du coût pour atteindre une position, nous allons utiliser une champ cout de type HashMap<Position,Integer> que nous allons initialiser dans le constructeur. De plus, on précisera que le coût de la position initiale de Pacman est 0.
Dans le constructeur, initialisez aussi une file à priorité PriorityQueue (qui sera un champ et que vous appellerez toVisit) pour que la priorité soit donnée par la distance de Manhattan additionnée au coût de la position (HashMap créer au-dessus). Pour utiliser une PriorityQueue, nous allons utiliser son constructeur qui demande en paramètre une référence sur un objet qui met en œuvre l'interface Comparator: @FunctionalInterface public interface Comparator<T> { int compare(T o1, T o2); } Pour cela trois possibilités s'offrent à vous :
- Écrire une nouvelle classe qui met en œuvre l'interface Comparator, et créer un objet de cette classe, puis passer la référence sur cet objet en paramètre du constructeur de PriorityQueue
- Passer en paramètre du constructeur de PriorityQueue la référence obtenue par la création d'une classe anonyme qui met en œuvre l'interface Comparator
- Passer en paramètre du constructeur PriorityQueue la référence obtenue par une expression lambda qui met en œuvre l'interface Comparator
Votre lambda expression sera de la forme: (position1, position2) -> Integer.compare(valeur heuristique position1, valeur heuristique position2) Donc les instructions pour créer la PriorityQueue auront la forme suivante : toVisit = new PriorityQueue( (position1, position2) -> Integer.compare(valeur heuristique position1, valeur heuristique position2)); );
Visualizer votre recherche.
N'oubliez pas de mettre à jour cost quand on rencontre un état pour la première fois.
Pour cela, les champs que nous avons utilisés deviendront des variables. Nous devrons aussi nous rappeler comment chaque Position a été atteinte, c'est-à-dire conserver une HashMap nous indiquant la position précédente dans l'exploration de chaque position.
Précédemment, chooseAction était appelée à chaque fois que nous voulions explorer une nouvelle position. Maintenant, il va falloir faire une boucle qui continue tant qu'il y a des états à explorer (!toVisit.isEmpty()) et que nous n'avons pas atteint la position finale.
Après la boucle, il va falloir reconstituer un chemin de la position initiale à la position finale. On pourra pour cela utiliser une LinkedList.
Un Pacman intelligent (∼1h – moyen – obligatoire)
Dans cet exercice, nous ne considérons plus qu'il n'y a qu'une seule nourriture à trouver. Nous voulons ramasser toutes les nourritures du monde de Pacman, et nous désirons le faire de la manière la plus rapide possible.
Encore une fois, les algorithmes sont similaires car nous pouvons représenter toutes les manières d'explorer l'univers de Pacman par un graphe où les nœuds sont des états et les transitions les actions légales entre les états.
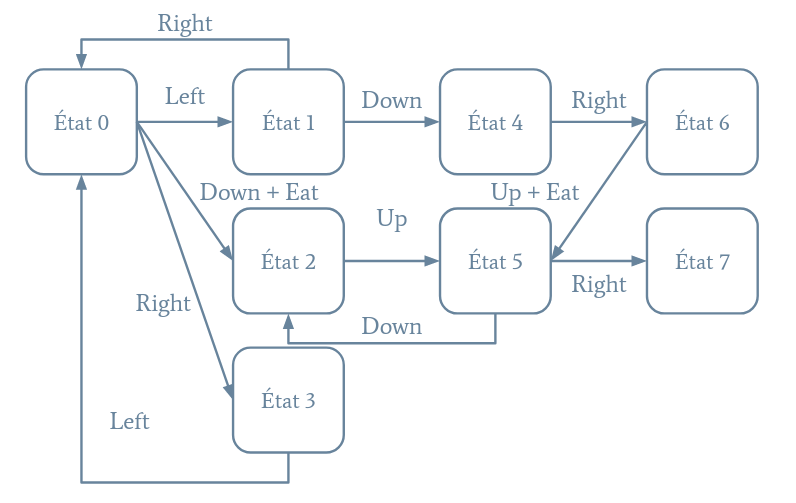
Ici, il est important de remarquer que nous allons en bas puis en haut, nous ne retournons pas forcément dans le même état. En effet, si de la nourriture est mangée pendant le déplacement, l'état est différent.
Comme précédemment, nous avons besoin d'une heuristique pour évaluer non plus une position, mais un état. Écrivez une fonction int calculateHeuristic(PacmanState state) qui pour l'instant retourne le nombre de nourritures restant.
Attention, un plan est toujours constitué d'une séquence de positions, même si l'on raisonne à l'échelle des états.
Voici quelques exemples de mondes sur lesquels tester votre code:
Pour concevoir une bonne heuristique, essayez de voir quels sont les critères ou les métriques qui donnent une idée si un état est meilleur qu'un autre.
Idées de métriques : La distance minimale à une nourriture, la distance maximale entre deux nourritures.
Que remarquez-vous ? Pourquoi ?
Ghost Buster ! (∼30min – moyen – entraînement)
Le but de cet exercice est de rajouter les fantômes à notre état et à notre simulateur pour avoir un vrai jeu de Pacman.
- Pour le constructeur avec uniquement la position de Pacman et le monde, on considère qu'il n'y a pas de fantôme.
- Pour le constructeur lisant à partir d'une String, nous introduisons un nouveau caractère pour les fantômes: G.
- findPossibleMoves pour qu'un déplacement sur un fantôme ne soit plus permis.
- move pour bien copier les fantômes dans le nouvel état.
- isFinalState qui doit maintenant retourner vrai quand Pacman meurt, c'est-à-dire quand il est sur la même case qu'un fantôme.
- equals qui doit prendre en compte les fantômes pour l'égalité entre états.
- hashCode qui doit ajouter le hash des positions des fantômes.
En réalité, il faut seulement modifier le tableau des positions des fantômes. Parcourez ce tableau et modifier la position du premier fantôme à la position from pour qu'il soit à la position to.
Nous allons représenter le joueur actuel avec un entier. L'entier 0 représente Pacman, et l'entier i représente le fantôme i - 1. Ajoutez cet attribut currentPlayer et modifiez les constructeurs pour l'initialiser. Écrivez ensuite un getter (getCurrentPlayer).
Enfin, vous devez modifier les méthodes move et moveGhost pour mettre à jour le joueur actuel.
J'ai vu un fantôme... (∼20min – moyen – entraînement)
Cet exercice a pour but de modifier notre boucle de jeu pour gérer les fantômes.
Créer un nouveau constructeur de PacmanSimulator permettant de prendre en plus des autres arguments un Ghost que l'on stockera dans les attributs.
- Demander à tour de rôle à chaque fantôme de bouger et modifier à chaque fois l'état actuel.
- Quand on sort de la boucle après avoir atteint un état final, nous devons afficher le score si nous avons gagné. Sinon, nous afficherons un message nous disant que nous avons perdu ainsi que le nombre de nourritures restantes.
Implémenter un fantôme direction GhostDirectional.
On fera attention que, dans notre cas, il faudra que GhostDirectional se souvienne de la direction précédente de chaque fantôme séparément.
Vérifiez le comportement de vos fantômes.
It's alive! (∼60min – difficile – entraînement)
Dans cet exercice, nous allons voir trois algorithmes permettant de prendre des décisions et de vraiment créer une intelligence artificielle. Ces algorithmes sont très largement utilisés aujourd'hui et des IAs comme AlphaZero sont basés sur eux.
L'idée de l'algorithme Minimax est que nous avons deux types d'agents : les agents max qui cherche à maximiser le score (Pacman) et les agents min qui cherchent à le diminuer (les fantômes). Cela signifie qu'un agent max choisira toujours l'action qui mène vers l'état avec le score le plus haut alors qu'un agent min choisira l'action qui mène vers l'état avec le score le plus bas. Le schéma suivant illustre le processus.
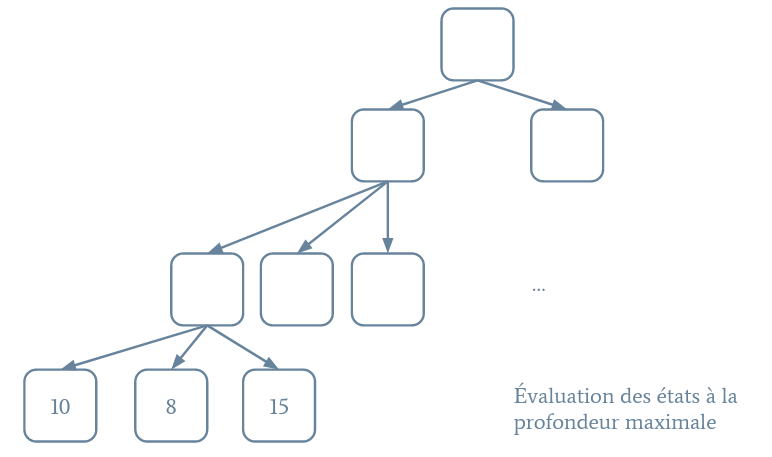
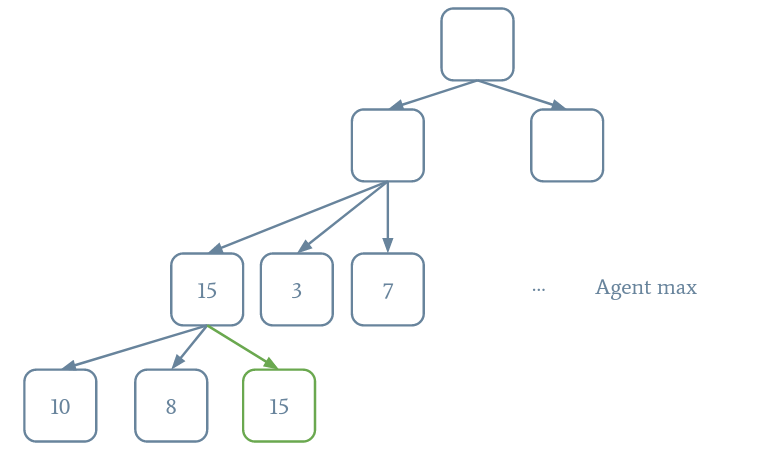
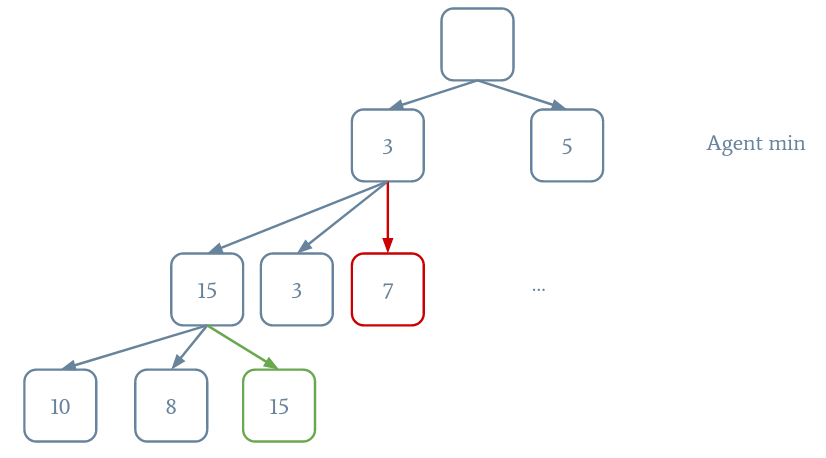
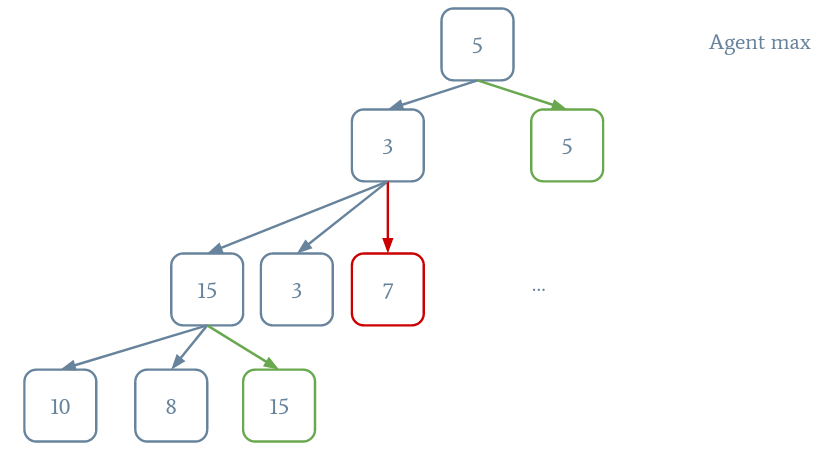
Pour commencer, créez une classe PacmanMinimax qui met en œuvre Pacman et dont le constructeur prend la profondeur en argument. En vous inspirant de la fonction implémentée pour A*, écrivez une fonction calculateHeuristic qui retourne le score d'un état, sachant que plus le score est haut, meilleur est l'état. De plus, on fera attention de donner des scores très hauts en cas de victoire et des scores très bas en cas de défaite.
Testez votre Pacman Minimax avec différente profondeur. Il devrait mieux survivre maintenant.
Pourquoi le temps de calcul augmente-t-il avec la profondeur ? Donnez la complexité en fonction de la profondeur.
Trouvez une profondeur donnant des temps de calculs raisonnables.
Cela nous permet de dériver un algorithme appelé l'élagage AlphaBeta qui est une optimisation de Minimax. En voici le pseudo-code:
Au début, alpha et beta sont initialisés à Integer.MIN_VALUE et Integer.MAX_VALUE.
Implémentez dans une classe PacmanAlphaBeta alphabeta puis utilisez cette méthode dans chooseAction.
Quelle est la complexité de alphabeta ? Observez-vous une plus grande vitesse de calcul par rapport à Minimax pour des profondeurs identiques ?
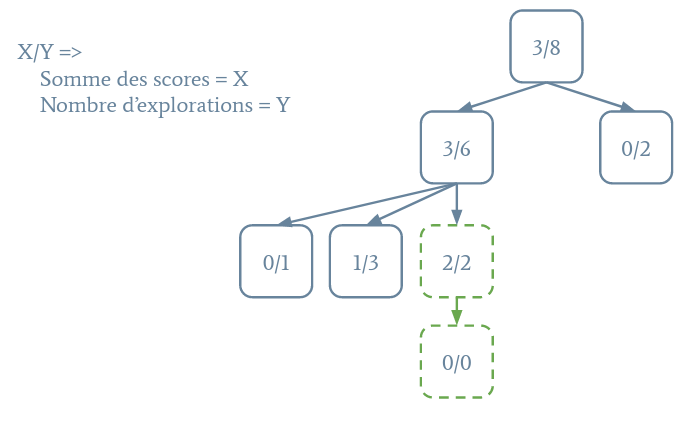
En réalité, MCTS ne consiste pas uniquement en des simulations aléatoires. Nous avons aussi un arbre "dur" d'états pour lesquels nous avons une estimation du score. À chaque itération de l'algorithme, nous allons choisir une feuille de l'arbre des états à partir de laquelle nous allons faire les simulations. Ce choix est un compromis entre explorer de nouveaux nœuds ou essayer d'affiner davantage l'évaluation du score. Ensuite, pour ce nœud, nous ajoutons tous ses fils à l'arbre et exécutons une simulation aléatoire. La simulation s'exécute jusqu'à un état final ou une profondeur maximale. L'état est alors évalué et son score est propagé dans l'arbre.
Un arbre MCTS est illustré dans la figure suivante :
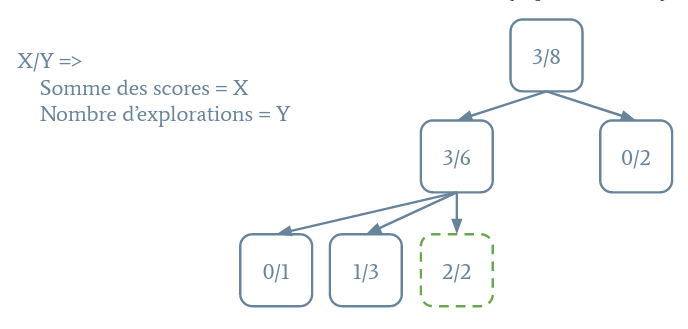
Commencez par créer un nœud de cet arbre appelé MCTSNode. Son constructeur prendra soit uniquement un état (nœud racine) que l'on stockera dans un champ PacmanState state;, soit un état et le nœud parent, que l'on stockera dans un champ MCTSNode parent. Ensuite, la classe contiendra deux attributs pour calculer le score moyen : double totalScore et int totalVisits. Initialisez-les.
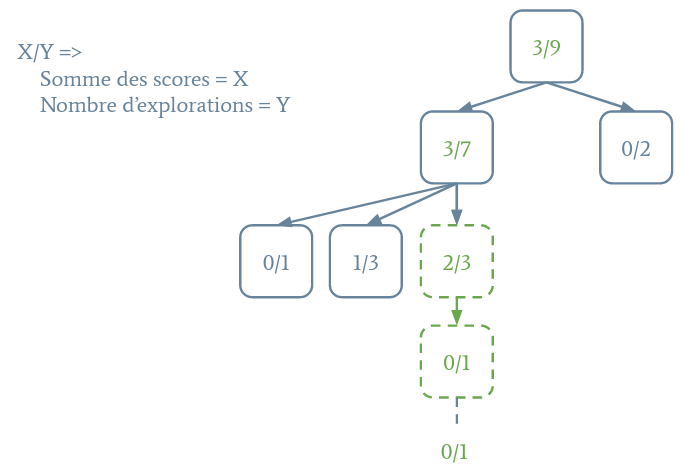
Le score moyen est donné par totalScore / numberVisits.
Le nœud racine n'a pas de parent, c'est-à-dire l'attribut parent est null.
Cette métrique est composée de deux parties : La première est simplement le score moyen du nœud. La deuxième permet de contrôler l'exploration de nœuds moins visités à l'aide de la constante C.
Pour sélectionner le nœud source de la simulation, on sélectionne successivement le fils avec le plus fort UCB (en fonction de C), jusqu'à atteindre une feuille. Par contre, nous considérerons que le score est totalScore si l'agent actuel est Pacman et -totalScore sinon (comme pour Minimax, les fantômes choisissent la pire action pour Pacman).
Commencez par rajouter un attribut List<MCTSNode> sons à MCTSNode. Celui-ci vaut null pour une feuille. Ensuite, écrivez une fonction MCTSNode selectLeaf(double C) qui implémente ce mécanisme de sélection.
- MCTSNode selectSon(double C)
- boolean isLeaf()
- double getUCB(double C, int totalParents)
 Écrivez la méthode void generateSons() qui va rajouter les fils au nœud actuel en fonction de l'agent
actuel. On modifiera l'attribut sons créé plus haut.
Écrivez la méthode void generateSons() qui va rajouter les fils au nœud actuel en fonction de l'agent
actuel. On modifiera l'attribut sons créé plus haut.
N'hésitez pas à créer des sous-fonctions List<MCTSNode> getSonsPacman() et List<MCTSNode> getSonsGhosts(Position positionGhost).
- Le nombre de nourritures restantes * -1 pour un état non final.
- Le score pour une victoire.
- Le nombre de nourritures restantes * -2 pour une défaite.
Quand nous avons le score, nous pouvons mettre à jour le score du nœud actuel avec la méthode addScore.
Écrivez une méthode void runSimulation(int maxDepth) effectuant la simulation et mettant à jour les scores.
N'oubliez pas de faire jouer Pacman et les fantômes.
Dans chooseAction, on crée un nouvel arbre et tant qu'il reste du temps, on sélectionne une feuille, on l'étend, et on lance une simulation depuis un des fils.
chooseAction retourne la position de Pacman de l'état du fils de la racine avec la meilleure moyenne.
On pourrait avoir un HashMap<PacmanState, MCTSNode> stateToNode dans les attributs et faire attention de supprimer le parent du nouveau nœud racine.

