CSC 3101 – Algorithmique et langage de programmation

CI7 : À la recherche de Bilbao

L'objectif de ce TP est d'étudier les listes doublement chaînées circulaires, les tables de hachages et les génériques en Java.

Durée des exercices obligatoires : 2h30 en présentiel + 45mn en hors présentiel

Exercice 1 : obligatoire (facile, ∼40mn)
Exercice 2 : obligatoire (difficile, ∼1h)
Exercice 3 : obligatoire (moyen, ∼30mn)
Exercice 4 : obligatoire (moyen, ∼20mn)
Exercice 5 : entraînement (moyen, ∼45mn)
Exercice 6 : entraînement (difficile)
Exercice 7 : entraînement (difficile)
Exercice 8 : entraînement (difficile)
Exercice 9 : entraînement (difficile)

Avant de pouvoir partir en vacances à Bilbao, il faut être capable de retrouver les coordonnées GPS d'une ville à partir de son nom. En effet, dans le CI5, notre application manipule directement les structures de données représentant les villes, mais notre application devrait avant être capable de retrouver ces structures de données lorsque l'utilisateur saisit des noms de villes dans l'interface.

De façon générale, une structure associant des clés à des valeurs s'appelle une table d'associations (aussi appelé dictionnaire ou encore map en anglais). Dans cet exercice, notre table d'associations associe des noms de ville (les clés) à des coordonnées GPS (les valeurs). Les tables d'associations sont omniprésentes en informatique. Ces tables sont, par exemple, utilisées par de nombreux serveurs Web comme Facebook, Google ou Amazon afin de retrouver les données associées à un utilisateur à partir de son identifiant de connexion. Vous avez même déjà mis en œuvre une table d'associations en utilisant un arbre binaire de recherche lorsque vous avez conçu la banque Lannister en CI4 : cette structure nous servait à retrouver un compte en banque (une valeur) à partir d'un nom d'utilisateur (une clé).

Dans ce TP, nous étudions une nouvelle mise en œuvre de la table d'associations : la table de hachage (hashmap en anglais). La table de hachage est une structure de données particulièrement efficace. Dans le meilleur cas, elle permet de retrouver une valeur à partir de sa clé en un temps constant (c.-à-d. Indépendamment du nombre d'éléments dans la table). Le pire cas est proportionnel au nombre d'éléments et le cas moyen est en général proportionnel à une racine n^ième du nombre d'éléments, où n est une constante dépendante de la mise en œuvre.

Abstraitement, une table de hachage est un tableau de taille infinie contenant des couples clés/valeurs. Le principe est d'associer un numéro unique à chaque clé. Ce numéro s'appelle le code de hachage de la clé et correspond à l'entrée à laquelle se trouve le couple clé/valeur associé à la clé dans le tableau. La figure ci-dessous, dans laquelle seules les valeurs sont représentées, illustre le précepte. À partir de la clé K, on calcule le code de hachage N qui est directement l'indice contenant le couple clé/valeur associé à la clé K dans le tableau.

      --------------------------------------------------- ......
Table | v0 | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 |      ......
      --------------------------------------------------- ......
                                 ^
             hash()              |
     clé K --------> code de hachage N  = indice dans le tableau

Concrètement, une table de hachage ne peut pas être infinie et il est difficile de garantir que deux clés différentes auront deux codes de hachage différents. Pour cette raison, il peut arriver que plusieurs couples clé/valeur se retrouvent dans la même case du tableau. De façon à gérer ces collisions, chaque entrée du tableau stocke en fait une liste d'associations clés/valeurs secondaire. Comme présenté sur la figure ci-dessous, pour trouver la valeur associée à la clé k5, il faut d'abord calculer le code de hachage H de la clé (dans notre exemple, ce code vaut 7, la façon de calculer les codes de hachage est discuté dans l'exercice 1). Ensuite, l'entrée à laquelle se trouve la clé k5 est H modulo la taille du tableau (dans notre exemple, l'entrée est 2). Comme il peut y avoir des collisions lorsque plusieurs clés sont associées à cette entrée, l'entrée contient une liste d'association clés/valeurs. Il suffit alors de chercher k5 dans cette liste pour retrouver la valeur v5 associée à k5.

                           [k6, v6]
                              ^
                              |
         [k2, v2]          [k5, v5]
            ^                 ^
            |                 |
         [k1, v1] [k3, v3] [k4, v4]          [k7, v7]
            ^        ^        ^                 ^
            |        |        |                 |
        ----------------------------------------------
Table   |        |        |        |        |        |
        ----------------------------------------------
                              ^
                              |
                              ----------------------
                                                   |
Clé k5 => code hachage 7 => 7 mod taille tableau = 2
       => cherche k5 dans la liste à l'entrée 2
       => renvoie v5

Si le tableau a une taille suffisamment grande et si la probabilité de collision entre codes de hachage est faible, les listes référencées par la table contiennent au plus une unique entrée. L'algorithme met donc un temps constant, indépendant du nombre d'éléments se trouvant dans la table de hachage, pour trouver une valeur à partir d'une clé. Dans la plupart des mises en œuvre, on a toutefois des tailles de liste égales en moyenne à une racine n^ième du nombre d'éléments (où n est une constante dépendante de la mise en œuvre), ce qui offre des performances très satisfaisantes.

Les identifiants de villes et les positions (∼40mn – facile – obligatoire)

Dans ce premier exercice, nous mettons en œuvre les clés (les identifiants de ville) et les valeurs (les positions GPS). La table de hachage que nous concevons dans les exercices suivants associera chaque identifiant de ville à une position.

Après avoir créé le projet gps, créez une classe Main contenant la méthode statique main dans le package tsp.gps.

Une clé est une instance de la classe CityId. Cette classe possède un unique champ privé de type chaîne de caractères nommé name qui identifie de façon unique une ville. Dans le package tsp.gps, créez la classe CityId avec son champ name. Ajoutez à cette classe :

un constructeur permettant d'initialiser le nom de la ville,
et une méthode String toString() renvoyant le nom de la ville.

Dans la méthode main créez une instance de CityId et vérifiez que la méthode toString() permet d'afficher correctement l'instance.

CityId0.java

Ajoutez une classe nommée Location dans tsp.gps définissant les champs privés latitude et longitude de type double. Ajoutez à cette classe :

un constructeur permettant d'initialiser ces champs,
et une méthode toString() renvoyant la chaîne de caractères "lat, long", dans laquelle lat correspond à la latitude et long à la longitude.

Dans la méthode main créez une instance de Location et vérifiez que la méthode toString() permet d'afficher correctement l'instance.

Location.java

La classe CityId va nous servir de clé. Il faut donc être capable de comparer deux instances de CityId pour savoir si elles sont égales. À cette question, nous nous occupons de savoir ce que signifie l'égalité entre CityId. Commencez par supprimer tout le code se trouvant dans la méthode main et copiez-collez le code suivant à la place :

CityId evry1 = new CityId("Evry");
CityId evry2 = new CityId("Evry");

Ensuite, affichez le résultat de la comparaison de evry1 avec evry2 avec l'opérateur ==. Pour quelle raison l'opérateur d'égalité renvoie-t-il faux ?

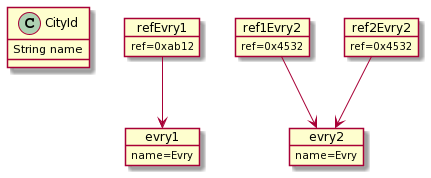
Car l'opérateur == effectue une comparaison par référence, c'est-à-dire qu'il compare la référence evry1 et evry2. Ces deux variables référençant deux objets différents, le résultat est faux. La question suivante explique en détail le problème.

Dans notre exercice, nous sommes intéressés par comparer le contenu des instances de CityId de façon à identifier que evry1 et evry2 sont bien deux identifiants pour la même ville. Cette comparaison des contenus s'appelle la comparaison par valeur, qui est à mettre en opposition à la comparaison par référence effectuée par l'opérateur ==. En effet, la comparaison par référence se cantonne à comparer les références de façon, à savoir si elles référencent bien le même objet.

Comparaison par référence versus comparaison par valeur.

La figure illustre la différence entre une comparaison par référence et une comparaison par valeur. L'état présenté résulte de l'exécution du code suivant :

CityId refEvry1 = new CityId("Evry");
CityId ref1Evry2 = new CityId("Evry");
CityId ref2Evry2 = ref1Evry2;

Les référence refEvry1 et ref1Evry2 sont différentes lorsqu'on effectue une comparaison par référence avec == puisque ces variables référencent deux objets différents (0xab12 est différent de 0x4532). En revanche, ref1Evry2 et ref2Evry2 sont bien égales lorsqu'on effectue une comparaison par référence avec == puisque ces deux variables référencent bien le même objet (les deux variables référencent l'objet 0x4532).

Une comparaison par valeur indique si deux objets sont similaires dans un sens défini par le développeur. Dans notre cas, deux instances de CityId sont égales si elles possèdent des champs noms constitués des mêmes lettres. C'est le cas des objets référencés par refEvry1 et ref1Evry2 dans la figure.

Comme on pourrait imaginer ajouter d'autres champs non significatifs pour la comparaison, Java ne peut pas deviner comment comparer les valeurs de deux objets. Pour cette raison Java ne fournit pas d'opérateur spécifique permettant d'effectuer une comparaison par valeur. À la place, la classe Object définit une méthode de comparaison par valeur boolean equals(Object o) générique qui peut donc être spécialisée par n'importe quelle classe puisque toutes les classes héritent de Object.

De façon à effectuer une comparaison par valeur, ajoutez une méthode public boolean equals(Object o) à la classe CityId. Cette méthode doit déjà vérifier que o est bien du type CityId en utilisant l'opérateur Java instanceof. Ensuite, si c'est le cas, cette méthode doit trans-typer vers le bas (downcast) o en CityId et renvoyer vrai si les champs name de this et o sont égaux.

De la même façon qu'une comparaison par référence de nos CityId renvoie faux, une comparaison par référence de leur champ name peut aussi renvoyer faux si le contenu des chaînes des caractères sont les mêmes, mais que les objets référencés sont différents. Pour cette raison, lorsque vous comparez le champ name de this avec celui de o, utilisez la méthode d'instance String.equals qui a été redéfinie dans la classe String afin d'effectuer une comparaison par valeur (techniquement, cette méthode vérifie que les caractères constituant les chaînes sont égaux).

public boolean equals(Object o) { if(o instanceof CityId) { return name.equals(((CityId)o).name); } else { return false; } }

Vérifiez que evry1.equals(evry2) renvoie vrai, que evry1.equals(new CityId("Paris")) renvoie faux et que evry1.equals("Evry") renvoie aussi faux.

Comme expliqué précédemment, il faut être capable de calculer la clé de hachage d'une clé. Nous enrichissons donc la classe CityId de façon à calculer son code de hachage. La classe Object définit une méthode d'instance générique public int hashCode() dédiée au calcul de code de hachage. Nous vous proposons donc de spécialiser cette méthode dans CityId.

Comme code de hachage, nous pourrions renvoyer n'importe quelle valeur, pourvu que les codes de hachage de deux objets égaux dans le sens comparaison par valeur (on vous rappelle que dans notre cas, deux clés sont égales si elles ont les mêmes noms de villes) soient égaux. En effet, cet invariant est fondamental : si deux clés égales k1 et k2 avaient des codes de hachage h1 et h2 différents, la recherche de k2 dans l'entrée h2 du tableau de hachage ne permettrait pas de retrouver la clé k1 se trouvant à l'entrée h1.

De façon à assurer l'unicité du code de hachage de deux clés différentes, et de façon à assurer que les collisions de code de hachage sont rares, nous vous proposons de réutiliser la méthode d'instance hashCode() de la classe String (cette méthode effectue des additions et des opérations binaires à partir des numéros des caractères constituant la chaîne de caractères). Notre méthode d'instance CityId.hashCode() doit donc simplement renvoyer le résultat de l'appel à hashCode() sur le champ name d'une instance de CityId.

Dans votre méthode main, vérifiez que evry1 et evry2 ont bien le même code de hachage.

public int hashCode() { return name.hashCode(); }

La liste doublement chaînée circulaire (∼1h – difficile – obligatoire)

Avant de se lancer dans la mise en œuvre d'une table de hachage complète, nous commençons par gérer la liste permettant de stocker les clés qui entrent en collision dans la table de hachage. Cette liste est elle-même une table d'associations puisqu'elle associe aussi des clés et des valeurs.

Nous vous proposons de construire cette liste à partir d'une liste doublement chaînée circulaire. Dans cet exercice, nous concevons la liste doublement chaînée circulaire. Nous nous préoccupons de la transformer en table d'associations dans l'exercice suivant, et nous finissons par construire la table de hachage complète dans les deux exercices qui suivent.

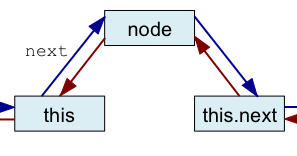
Une liste doublement chaînée circulaire est une liste chaînée circulaire, c'est-à-dire que le dernier nœud référence le premier nœud. C'est aussi une liste doublement chaînée, c'est-à-dire qu'un nœud possède une référence avant (next) comme dans une liste chaînée classique, mais aussi une référence arrière (prev) vers le nœud qui le précède dans la liste. Comparée à la liste simplement chaînée non circulaire que vous avez vue en CI3, la liste doublement chaînée circulaire rend le code de suppression d'un nœud beaucoup plus simple.

Une liste doublement chaînée.

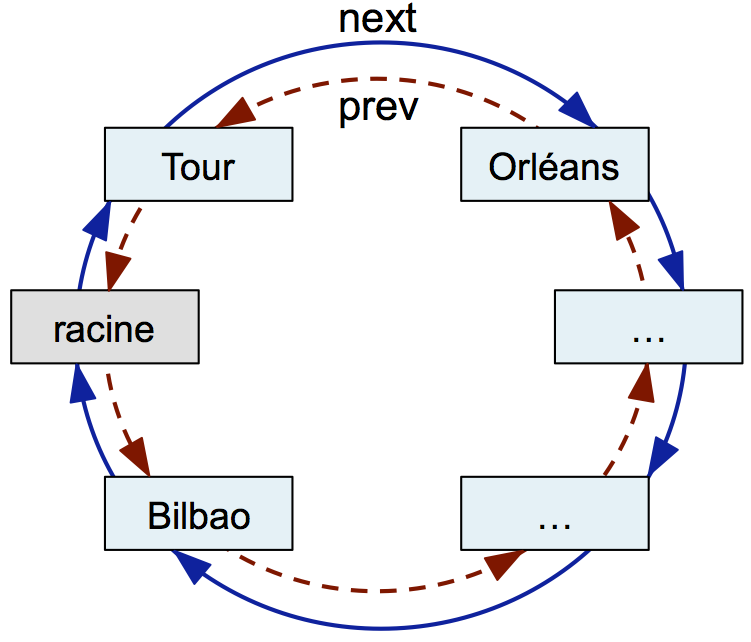
La figure ci-dessus présente une liste doublement chaînée circulaire de villes. Le premier nœud (en gris) s'appelle le nœud racine. Il représente un point d'entrée dans la liste. Les flèches pleines en bleu représentent les références vers l'avant (next) et les flèches rouges en pointillé représentent les références vers l'arrière (prev). Si on suit les références vers l'avant, on voit que la racine référence la première ville, ici Tours. Ensuite, une chaîne de ville permet d'atteindre la dernière ville, ici Bilbao. Enfin, la dernière ville référence la racine pour rendre la liste circulaire. De façon similaire, on peut parcourir la liste dans le sens inverse en suivant le chaînage prev.

Commencez par créer un nouveau package nommé tsp.hashmap (sous Eclipse, File->New->Package). Ce package nous sert à stocker les classes qui modélisent les tables d'associations, alors que le package tsp.gps (voir exercice précédent) nous sert à stocker les classes de l'application associant des villes à des coordonnées GPS.

Ajoutez une classe nommée ListMap au package tsp.hashmap. Cette classe associe des clés à des valeurs et doit donc être paramétrée par deux types génériques : le type K donne le type de la clé alors que le type V donne le type de la valeur. La classe ListMap représente un des nœuds de la liste doublement chaînée circulaire. Elle doit donc posséder les champs privés next, prev, key et value.

Pour être précis, les champs de ListMap sont :

ListMap<K, V> next référence le nœud suivant de la liste,
ListMap<K, V> prev référence le nœud précédent de la liste,
K key référence la clé associée au nœud,
V value référence la valeur associée au nœud,

ListMap0.java

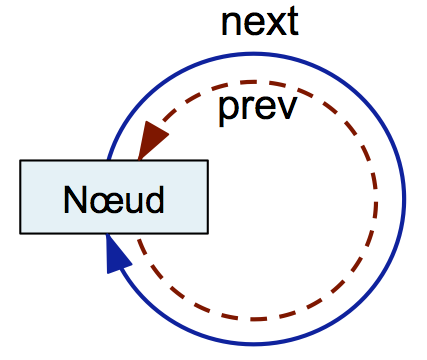
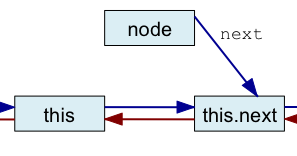
Ajoutez un constructeur à ListMap permettant d'initialiser un nœud de la liste chaînée. Ce constructeur doit prendre en argument une clé et une valeur et les affecter aux champs adéquats. Ce constructeur doit aussi initialiser les références next et prev de façon à ce que le nœud alloué soit une liste doublement chaînée circulaire constituée d'un unique nœud. La figure ci-dessous illustre cet état initial.

Une liste chaînée avec un unique nœud.

ConstructeurListMap.java

Ajoutez une méthode String toString() à la classe ListMap. Cette méthode doit renvoyer la chaîne de caractère (k, v), dans laquelle k est remplacé par l'appel à toString() sur la clé et v par l'appel à toString() sur la valeur.

public String toString() { return "(" + key + ", " + value + ")"; }

Dans la méthode main, allouez une instance de ListMap paramétrée de façon à associer des CityId à des Location. Initialisez cette instance avec le CityId et le Location que vous avez déjà créés à l'exercice précédent. Comme la classe ListMap n'est pas dans le même package que la classe Main, on vous rappelle que pour importer une classe X d'un package a.b.c, il faut mettre import a.b.c.X; dans l'entête du fichier Java.

Finalement, affichez sur le terminal cette instance de ListMap, et vérifiez que vous obtenez bien un affichage similaire à celui-ci :

(Toulouse, 43.604652, 1.4442090000000007)

Nous écrivons maintenant une méthode permettant d'insérer un nœud dans une liste circulaire doublement chaînée. Pour le moment, nous ne nous soucions pas d'assurer l'unicité des clés, ce sera le sujet d'une prochaine question. Ajoutez une méthode d'instance append prenant en paramètre une clé et une valeur. Cette méthode insère un nœud associant la clé à la valeur passée en paramètre après le receveur de l'appel (this).

La série de figures ci-dessous illustre l'algorithme que vous devez mettre en œuvre où node est le nouveau nœud à insérer dans la chaîne.


Avant insertion	Première étape	Seconde étape	Troisième étape	Quatrième étape

node.next = this.next

node.prev = this

this.next.prev = node

this.next = node

public void append(K key, V value) { ListMap<K, V> node = new ListMap<>(key, value); node.prev = this; node.next = next; next.prev = node; next = node; }

Comme présenté dans la figure au début de l'exercice, une liste doublement chaînée circulaire possède une racine. Ce nœud racine est un faux nœud, c'est-à-dire qu'il ne stocke pas de clé ou de valeur. Il ne sert que de point d'entrée dans la liste, même quand la liste est vide. Il s'agit techniquement d'un nœud référençant la clé null et la valeur null.

De façon à préparer les tests suivants, commencez par supprimer tout le code qui se trouve dans la méthode main. À la place, créez un nœud racine nommé root et utilisez append pour ajouter au moins 3 villes avec des coordonnées quelconques. Si, lorsque vous lancez votre programme, Eclipse vous signale l'erreur NullPointerException, cela signifie que le code de append est incorrect et il faut que vous recommenciez la question f.

Ajoutez une méthode void display() à la classe ListMap permettant d'afficher les couples clé/valeur de chacun des nœuds de la liste. Cette méthode considère que le receveur de l'appel est une racine et n'affiche donc pas son contenu. En revanche, elle affiche le résultat de l'appel à toString() sur chacun des nœuds de la liste. Vérifiez que votre code est correct en appelant display sur la liste root que vous avez construite à la question précédente. Vous devriez obtenir un affichage similaire à celui-ci :

List: 
  (Bilbao, 43.2630126, -2.9349852000000283)
  (Panpelune, 42.812526, -1.645774500000016)
  (San Sebastien, 43.318334, -1.9812312999999904)
  (Bayonne, 43.492949, -1.4748409999999694)

Pensez que si vous avez des erreurs, elles peuvent venir de display, mais aussi de append.

Pour vous guider, vous pouvez parcourir la liste en écrivant une boucle qui commence avec le premier nœud après la racine, qui suit les références next, et qui s'arrête quand la racine est atteinte.

public void display() { System.out.println("List: "); for(ListMap<K, V> cur=next; cur!=this; cur=cur.next) System.out.println(" " + cur); }

La table d'associations basée sur les listes (∼ 30mn – moyen – obligatoire)

Dans cet exercice, nous terminons notre mise en œuvre de la liste doublement chaînée circulaire de façon à la transformer en table d'associations.

Ajoutez à la classe ListMap une méthode ListMap<K, V> lookupNode(K key) permettant de retrouver un nœud associé à la clé key dans la liste. Cette méthode doit parcourir la liste, un peu comme vous l'aviez fait dans la méthode display. Si pendant le parcours, vous trouvez un nœud avec une clé égale (dans le sens comparaison par valeur, c'est-à-dire en utilisant equals) au paramètre de la méthode, il faut renvoyer ce nœud, sinon, il faut renvoyer la valeur null.

Dans la méthode main, vérifiez que votre code est correct en essayant (i) de trouver le nœud associé à l'une de vos villes dans la liste root, et (ii) de trouver une ville qui n'y est pas.

public ListMap<K, V> lookupNode(K key) { for(ListMap<K, V> cur=next; cur!=this; cur=cur.next) if(cur.key.equals(key)) return cur; return null; }

Ajoutez une méthode V get(K key) renvoyant la valeur associée à la clé key si elle existe et null sinon. Cette méthode peut bien sûr appeler lookupNode pour retrouver le nœud associé à key.

public V get(K key) { ListMap<K, V> node = lookupNode(key); if(node == null) return null; else return node.value; }

Ajoutez une méthode boolean remove(K key) permettant de supprimer une association et renvoyant vrai si et seulement si l'association existait avant l'appel. Cette méthode peut bien sûr appeler lookupNode pour retrouver le nœud associé à key. Dans la méthode main, supprimez l'une de vos villes et appelez display() pour vérifier que votre liste est correcte.

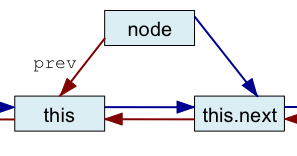
Pour supprimer un nœud N d'une liste doublement chaînée circulaire, il suffit que le prédécesseur de N joigne directement le suivant de N et réciproquement. Techniquement, il faut que le suivant du prédécesseur de N référence le suivant de N, et que le prédécesseur du suivant de N référence le prédécesseur de N.

public boolean remove(K key) { ListMap<K, V> node = lookupNode(key); if(node != null) { node.next.prev = node.prev; node.prev.next = node.next; return true; } else return false; }

Ajoutez une méthode boolean put(K key, V value) permettant d'ajouter l'association entre key et value. Si il n'existe pas d'association entre key et value, cette méthode doit créer une nouvelle association en appelant append et renvoyer vrai. Sinon, elle doit mettre à jour l'ancienne association en modifiant son champ valeur et renvoyer faux. Pensez que vous pouvez retrouver l'ancienne association, si elle existe, avec lookupNode.

public boolean put(K key, V value) { ListMap<K, V> node = lookupNode(key); if(node == null) { append(key, value); return true; } else { node.value = value; return false; } }

Afin de tester votre code, supprimez tout le code qui se trouve dans la méthode main. À la place, copiez-collez le code suivant :

ListMap<CityId, Location> map = new ListMap<>(null, null);

map.put(new CityId("Evry"), new Location(48.629828, 2.4417819999999892));
map.put(new CityId("Paris"), new Location(48.85661400000001, 2.3522219000000177));
map.put(new CityId("Le Mans"), new Location(48.00611000000001, 0.1995560000000296));
map.put(new CityId("Orléan"), new Location(47.902964, 1.9092510000000402));
map.put(new CityId("Angers"), new Location(47.478419, -0.5631660000000238));
map.put(new CityId("Tours"), new Location(47.39414399999999, 0.6848400000000083));
map.put(new CityId("Bourges"), new Location(47.081012, 2.398781999999983));
map.put(new CityId("Poitiers"), new Location(46.58022400000001, 0.34037499999999454));
map.put(new CityId("Limoges"), new Location(45.83361900000001, 1.2611050000000432));
map.put(new CityId("Angouleme"), new Location(45.648377, 0.15623690000006718));
map.put(new CityId("Bordeaux"), new Location(44.837789, -0.5791799999999512));
map.put(new CityId("Agen"), new Location(44.203142, 0.6163629999999785));
map.put(new CityId("Toulouse"), new Location(43.604652, 1.4442090000000007));
map.put(new CityId("Bayonne"), new Location(43.492949, -1.4748409999999694));
map.put(new CityId("Pau"), new Location(43.2951, -0.3707970000000387));
map.put(new CityId("San Sebastien"), new Location(43.318334, -1.9812312999999904));
map.put(new CityId("Panpelune"), new Location(42.812526, -1.645774500000016));
map.put(new CityId("Bilbao"), new Location(43.2630126, -2.9349852000000283));
			
map.display();

System.out.println(map.get(new CityId("Bilbao")));
map.remove(new CityId("Bilbao"));
System.out.println(map.get(new CityId("Bilbao")));

L'exécution de ce test devrait vous générer un affichage similaire à celui-ci :

List: 
  (Bilbao, 43.2630126, -2.9349852000000283)
  (Panpelune, 42.812526, -1.645774500000016)
  (San Sebastien, 43.318334, -1.9812312999999904)
  (Pau, 43.2951, -0.3707970000000387)
  (Bayonne, 43.492949, -1.4748409999999694)
  (Toulouse, 43.604652, 1.4442090000000007)
  (Agen, 44.203142, 0.6163629999999785)
  (Bordeaux, 44.837789, -0.5791799999999512)
  (Angouleme, 45.648377, 0.15623690000006718)
  (Limoges, 45.83361900000001, 1.2611050000000432)
  (Poitiers, 46.58022400000001, 0.34037499999999454)
  (Bourges, 47.081012, 2.398781999999983)
  (Tours, 47.39414399999999, 0.6848400000000083)
  (Angers, 47.478419, -0.5631660000000238)
  (Orléan, 47.902964, 1.9092510000000402)
  (Le Mans, 48.00611000000001, 0.1995560000000296)
  (Paris, 48.85661400000001, 2.3522219000000177)
  (Evry, 48.629828, 2.4417819999999892)
43.2630126, -2.9349852000000283
null

Finalement, nous encapsulons de façon un peu plus satisfaisante les méthodes de ListMap. En effet, utiliser directement append de l'extérieur n'est pas recommandé. La méthode append permet d'ajouter manuellement des nœuds, et ne permet pas d'assurer qu'une clé est associée à une unique valeur, ce qui risquerait d'entraîner des erreurs chez les utilisateurs de votre table d'associations. Pour cette raison, nous vous suggérons de rendre la méthode append privée. Vous pouvez aussi rendre lookupNode privé car cette méthode n'a pas vocation à être utilisée de l'extérieur de la classe.

Félicitations, vous venez de mettre en œuvre une structure de donnée connue pour être complexe !

L'interface d'une table d'associations (∼ 20mn – moyen – obligatoire)

Avant de mettre en œuvre les tables de hachages, nous abstrayons la notion de table d'associations sous la forme d'une interface.

Dans le package tsp.hashmap, ajoutez une interface nommée Map paramétrée par le type K d'une clé et le type V d'une valeur. Ensuite, ajoutez les méthodes suivantes à l'interface :

boolean put(K key, V value) : crée une association et renvoie vrai si la clé n'avait aucune association auparavant,
V get(K key) : renvoie la valeur associée à key si elle existe et null sinon,
boolean remove(K key) : supprime l'association de key et renvoie vrai si elle existait,
void display() : affiche toutes les associations de la table d'associations sur le terminal.

Enfin, modifiez la déclaration de ListMap afin qu'elle mette en œuvre Map. Si le code de ListMap est correct, vous ne devriez rien avoir à faire d'autre puisque les méthodes de l'interface Map sont déjà mises en œuvre dans ListMap.

Map.java

public class ListMap<K, V> implements Map<K, V>

Maintenant que nous avons une interface générique de table d'associations, nous pouvons nous en servir dans la méthode main. Au début du main, remplacez la déclaration :

ListMap<CityId, Location> map = new ListMap<>(null, null);

par

Map<CityId, Location> map = new ListMap<>(null, null);

de façon à s'assurer que le code de main n'utilise que l'interface d'une liste d'associations et ne dépend pas des détails de mise en œuvre. Vérifiez que votre code s'exécute toujours correctement.

La table de hachage (∼ 30mn – moyen – entraînement)

Maintenant que nous avons conçu toutes les classes et interfaces de base, nous pouvons enfin mettre en œuvre les tables de hachage. Techniquement, notre table de hachage est simplement un tableau de ListMap : les ListMap permettent de gérer les clés qui entrent en collision.

Dans le package tsp.hashmap, ajoutez une classe nommée HashMap paramétrée par le type K d'une clé et le type V d'une valeur. Cette classe doit mettre en œuvre l'interface Map. Dans un premier temps, laissez les mises en œuvre des méthodes de Map vides :

put renvoie toujours faux,
get renvoie toujours null,
remove renvoie toujours faux,
display ne fait rien.

HashMap0.java

Modifiez le code de main afin d'allouer une instance de HashMap au lieu d'une instance de ListMap. Vous ne devriez avoir besoin que de modifier la ligne qui alloue la table d'associations. Vérifiez que vous pouvez toujours lancer votre application qui devrait vous produire l'affichage suivant :

null
null

Une table de hachage est techniquement un tableau de Map dans lequel chaque élément référence une instance de ListMap. Ajoutez à HashMap un champ table référençant un tableau de Map. Dans le constructeur de HashMap, initialisez ce champ avec un tableau de 5 Map, puis initialisez chacune des entrées de ce tableau en allouant un nouveau ListMap pour chaque entrée.

private Map<K, V>[] table; public HashMap() { table = new Map[5]; for(int i=0; i<table.length; i++) table[i] = new ListMap(null, null); }

Pour mettre en œuvre put, get et remove, nous aurons besoin de connaître le ListMap dans lequel se trouve une clé. Par exemple, que ce soit pour ajouter une clé, trouver la valeur associée à une clé ou supprimer une clé, nous avons besoin de savoir que le ListMap dans lequel se trouve la clé k5 est à l'indice 2 dans la figure présentée au début de l'exercice. Écrivez une méthode intermédiaire Map<K, V> getList(K key) renvoyant une référence vers le ListMap dans lequel la clé key devrait se trouver.

En détail, getList doit :

Calculer le code de hachage H de key en appelant hashCode().
Effectuer un modulo de H avec la taille du tableau de hachage (table.length). Le résultat r de ce modulo devrait donner l'indice du TableMap dans le tableau table dans lequel key doit se trouver. Toutefois, en Java, le modulo d'un nombre négatif reste négatif et ne peut pas directement être utilisé comme indice dans table. Si ce modulo est négatif, il faut que vous y ajoutiez table.length pour le rendre positif.
Renvoyer le ListMap se trouvant à l'indice r de table.

private Map<K, V> getList(K key) { int code = key.hashCode() % table.length; if(code

Nous pouvons maintenant mettre en œuvre put, get et remove. Chacune de ces méthodes doit appeler getList pour retrouver le ListMap associé à la clé passée en paramètre, puis déléguer l'appel à la méthode adéquate de ListMap.

HashMapPutGetRemove.java

Complétez le code de HashMap.display. Il suffit d'invoquer display sur chaque élément du tableau. Vérifiez que l'affichage produit est similaire à celui de l'exercice 3.

public void display() { for(int i=0; i<table.length; i++) table[i].display(); }

Quelles sont les complexités des méthodes put, get et remove de HashMap dans le pire des cas ?

La méthode getList a une complexité constante, donc les complexités dépendent uniquement de ListMap. De même, dans ListMap, tout est en coût constant sauf lookupNode qui est utilisée une fois par chaque méthode. lookupNode itère à travers toute la liste dans le pire des cas, elle a donc une complexité linéaire en la taille de la liste dans le pire des cas.
Si nous revenons à HashMap, le pire des cas se produit si tous les hashs entrent en collision. Dans ce cas, une seule ListMap contient toutes les données et la complexité de toutes les opérations est linéaire en le nombre d'éléments dans le HashMap.

Le pire des cas se produit extrêmement rarement grâce aux propriétés des fonctions de hashage. Quelle la complexité dans le pire des cas en supposant que les clefs sont équitablement réparties dans la table.

Soit h la taille de la table interne et n le nombre d'éléments. Alors, la taille d'une ListMap est de n/h. Si l'on considère que n est du même ordre de grandeur que h, on a un temps constant.

Félicitations, vous venez d'écrire une superbe table de hachage réutilisable !

Le code que vous avez écrit est assez similaire à celui fourni par Oracle dans sa machine virtuelle Java.

Pour approfondir (entraînement)

Dans cet exercice, vous êtes libre de choisir l'implémentation qui vous voulez. Créez autant de champ et méthodes que vous le souhaitez, tout en essayant de conserver les principes de base de la programmation orientée objet comme l'encapsulation.
Si vous obtenez une implémentation différente de la nôtre, c'est tout à fait normal !

Pour éviter d'avoir trop d'éléments dans chaque ListMap, il est possible de redimensionner la taille du tableau interne. Écrivez une fonction resize qui double la taille du tableau interne.
Attention, il faut réinsérer tous les éléments !
On pourra ajouter un nouveau constructeur prenant en argument la capacité du tableau interne, c'est-à-dire sa taille. De plus, on pourra utiliser un HashMap temporaire et modifier le tableau interne au dernier moment.
Il peut être utile de rajouter dans Map une méthode addAllTo(HashMap<K, V> map) qui ajoute tous les éléments du Map actuel au HashMap. Cette solution temporaire nous permet de ne pas briser l'encapsulation. Nous verrons dans un prochain cours que nous pourrions utiliser des itérateurs à la place.

public void resize() { int newCapacity = this.table.length * 2; HashMap<K, V> newHashMap = new HashMap<>(newCapacity); for (int i = 0; i < this.table.length; i++){ this.table[i].addAllTo(newHashMap); } this.table = newHashMap.table; } public void addAllTo(HashMap<K, V> map) { for (int i = 0; i < map.table.length; i++){ map.table[i].addAllTo(this); } } public HashMap(int capacity) { table = new Map[capacity]; /* the only type unsafe operation of the application */ for(int i=0; i<table.length; i++) table[i] = new ListMap<>(null, null); }

Dans l'implémentation de Java, un redimensionnement a lieu lorsque le nombre d'éléments insérés dans le HashMap dépasse la capacité (c'est-à-dire la taille du tableau interne) * un "load factor". Ce load factor est égal à 0.75 en général.
Faites en sorte que le tableau se redimensionne automatiquement quand il atteint une certaine taille.
On pourra utiliser un champ size qui s'augmente à chaque ajout nouveau au HashMap et diminue à chaque retrait effectif.

private int size = 0; private final double loadFactor = 0.75; public boolean put(K key, V value) { boolean wasInMap = getList(key).put(key, value); if (wasInMap) size++; if (size > this.table.length * loadFactor) resize(); return wasInMap; } public boolean remove(K key) { boolean wasInMap = getList(key).remove(key); if (wasInMap) size--; return wasInMap; }

Quelle est la complexité resize ? Comment cela impacte-t-il la complexité des autres fonctions dans le pire des cas ?

La complexité de resize est linéaire en le nombre d'éléments. La complexité de put est impactée négativement : elle est maintenant tout le temps linéaire, quelle que soit la répartition des hashs. Par contre, get et remove sont maintenant à coût constant dans le cas de hashs équitablement répartis !

Estimez la complexité amortie de put dans le cas où les hashs sont équitablement répartis. On prendra un load factor de 1 pour simplifier.

Avec le redimensionnement du tableau interne, la complexité des opérations dans put est maintenant à coût constant mis à part resize. Cependant, cette fonction est appelée uniquement quand le tableau atteint le tableau se remplit la première fois ou double de taille dans les cas suivants. Le coût de resize est alors linéaire en la taille, ce qui nous donne un coût amorti constant !
La preuve formelle ressemble à celle du tableau extensible des TPs précédents.

Une structure de donnée très utile s'appelle le Set. Elle permet de stocker des éléments différents (à l'opposition des listes) et non ordonnés. Son but est de pouvoir rapidement ajouter et retirer des éléments, ainsi que vérifier la présence d'un élément. Son interface est la suivante :

boolean add(E element) : Ajoute un élément dans le set. On renvoie vrai si cet élément n'était pas déjà dans le set.
boolean remove(E element) : Supprime un élément dans le set. On renvoie vrai si cet élément était bien dans le set.
boolean contains(E element) : Renvoie vrai si cet élément est dans le set.

En utilisant la classe HashMap, écrivez la class HashSet implémentant l'interface Set.

L'implémentation de Java fonctionne en suivant le même principe.

File et pile ! (entraînement)

Dans cet exercice, nous allons voir deux structures de données très utiles qui peuvent être implémentées à partir d'une liste doublement chaînée : la file et la pile.

La file (ou Queue en anglais) est une structure de donnée qui permet d'ajouter des éléments et ensuite de les récupérer dans l'ordre d'ajout. C'est ce que l'on appelle une FIFO (first in, first out). Pour l'implémenter, nous allons nous inspirer de la liste doublement chaînée.
Créer une classe générique Queue. Cette classe fonctionnera de la même manière que la liste doublement chaînée. Elle aura deux constructeurs : un sans argument (ce qui créera une liste vide) et un autre avec un seul argument, ce qui crée une liste avec un seul argument. Comme pour la liste double chainée, nous retrouverons les attributs next, prev, et value (la clef n'est plus utile). Pour savoir si une liste est vide ou non, nous utiliserons un argument supplémentaire isEmpty.
Pour l'instant, isEmpty vaut true uniquement pour le constructeur sans argument.

Queue0.java

En vous inspirant de append pour la liste doublement chaînée, écrivez une fonction add. Cette fonction remplacera la valeur du nœud actuel par la nouvelle valeur et ajoutera dans le next un nouveau nœud avec l'ancienne valeur.
Si la file était vide, on ne remplacera que la valeur actuelle (et on mettra à jour isEmpty).

public void add(E value){ if (isEmpty){ this.value = value; this.isEmpty = false; } else { Queue<E> node = new Queue<>(this.value); node.prev = this; node.next = next; next.prev = node; next = node; this.value = value; } }

Écrivez une fonction remove qui retire la valeur du nœud actuel de la liste. Pour cela :

Si la file est vide, on retourne null.
Si la file ne contient qu'un seul nœud, on rend la file vide est on retourne la valeur actuelle.
Sinon, on retourne la valeur actuelle. Cependant, avant cela, on copie la valeur next sur le nœud actuel et on supprime le nœud suivant.

public E remove(){ if (isEmpty) return null; if (this.next == this){ isEmpty = true; return this.value; } E res = this.prev.value; if (this.prev == this.next){ this.next = this; } this.prev = this.prev.prev; return res; }

Testez votre code dans une fonction main.

Queue.java

En suivant la même procédure, écrivez une pile (ou Stack en anglais). Le principe est l'opposé de la file, on veut récupérer les éléments non pas dans l'ordre d'insertion, mais dans l'ordre inverse d'insertion. C'est ce que l'on appelle une LIFO (last in, first out).

Stack.java

Un moteur de recherche de documents (entraînement)

Dans cet exercice, nous allons mettre en place un moteur de recherche de documents. Pour cela, nous allons utiliser une métrique appelée TFIDF (voir plus loin).
Cet exercice vous laisse une certaine liberté sur l'implémentation, il est donc normal de ne pas retrouver exactement le même code que nous.
Vous aurez besoin de Map et de Set. Vous pouvez soit réutiliser votre implémentation, soit utiliser celle directement donnée par Java, aussi appelées HashSet et HashMap (faites attention aux imports).

Nous allons représenter un document par une classe Document avec un champ content. Créez cette classe à partir d'une String. On ajoutera également une fonction pour obtenir la représentation textuelle du document. Cette représentation sera la première ligne du document (c.f., la fonction split de String). Vous devriez utiliser la méthode String[] split(char c).

Document0.java

Le premier aspect de TFIDF est la fréquence des termes (TF = Term Frequency). Plus un terme apparait dans un document, plus il est important pour ce document.
Un terme est simplement un mot en minuscule. Écrivez une fonction preprocess qui retourne un tableau de String correspondant aux mots en minuscule dans le document (attention aux fins de lignes).
Par exemple, "Je suis un lion.\nJe mange de l'herbe." devient {"je", "suis", "un", "lion.", "je", "mange", "de", "l'herbe."}.
La documentation de String va vous aider. En particulier, les méthodes String toLowerCase() et String[] split(String regex).

public String[] preprocess(){ content = content.toLowerCase(); return content.split("[ \n]"); }

Calculer la fréquence d'un terme peut être coûteux pour un long document. Nous voulons donc pré-calculer cette fréquence et la stocker dans un champ HashMap<String, Double> frequencies. Faites en sorte que Document pré-calcule toutes les fréquences dans le constructeur. Ajoutez également une méthode pour accéder à la fréquence d'un terme.

On rappelle que la fréquence d'un terme est le nombre d'occurrences de ce terme dans le document divisé par le nombre de mots total.

Vous aurez sûrement besoin d'un HashMap.

DocumentFrequencies.java

Il y a quelques CIs, nous avons interdit l'usage de static en dehors de la fonction main. Si vous êtes arrivés ici, vous avez le droit de savoir la vérité sur static et comment l'utiliser dans une situation précise.
Imaginons que nous voulions maintenant rajouter la possibilité de créer un document à partir d'un fichier ou à partir d'une URL. Dans les deux cas, nous désirons donner un nom du fichier ou l'URL sous forme d'une String. Mais il y a un problème : le constructeur prenant en entrée une String est déjà pris. On pourrait imaginer d'autres solutions:

Rajouter des paramètres au constructeur pour dire si l'on passe le contenu, un nom de fichier ou une URL. Cependant, cette solution est très verbeuse et n'est pas très flexible (que faire si je veux rajouter une nouvelle manière de créer un document ?).
On pourrait étendre la classe document avec des classes filles DocumentURL et DocumentFile. Cependant, cette solution oblige à créer des classes uniquement dans le but de remplacer le constructeur, ce qui n'est pas forcément optimal.
On peut utiliser une fabrique (factory en anglais). Une fabrique est une méthode statique spécialisée dans la création d'objets. C'est un patron de conception classique qui a beaucoup d'avantages (c.f. le cours CSC 4102 – Introduction au génie logiciel pour applications orientées objet). Vous avez déjà rencontré des fabriques sans le savoir à travers la méthode Integer.valueOf(String s) qui permet de "fabriquer un entier" à partir d'une chaîne de caractères.

En général, les fabriques sont implémentées avec des méthodes statiques.
Nous donnons ici deux fonctions permettant de lire un document à partir d'un fichier ou d'une URL.

            private static String readFile(String filename){
                String content = "";
                try {
                    content = new String(Files.readAllBytes(Paths.get(filename)));
                } catch (IOException e) {
                    System.err.println("The file " + filename + " does not exist");
                    content = "";
                }
                return content;
            }

            public static String readStringFromURL(String requestURL) {
                try {
                    Files.createDirectories(Paths.get("cache_documents/"));
                } catch (IOException e) {
                    System.err.println("Problem while creating the cache file...");
                }
                String[] filenameSplit = requestURL.split("/");
                String filename = "cache_documents/" + filenameSplit[filenameSplit.length - 1];
                File f = new File(filename);
                if(f.exists() && !f.isDirectory()) {
                    return readFile(filename);
                }
                String res = "";
                try (Scanner scanner = new Scanner(new URL(requestURL).openStream(), StandardCharsets.UTF_8)) {
                    scanner.useDelimiter("\\A");
                    res = scanner.hasNext() ? scanner.next() : "";
                } catch (MalformedURLException e) {
                    System.err.println("Misformed URL");
                } catch (IOException e) {
                    System.err.println("Error Reading URL");
                }
                try {
                    BufferedWriter writer = new BufferedWriter(new FileWriter(filename, true));
                    writer.write(res);
                    writer.close();
                } catch (IOException e) {
                    System.err.println("Problem saving to cache...");
                }
                return res;
            }
        

Écrivez deux fabriques statiques fromFile et fromURL à partir des deux fonctions données au-dessus.

public static Document fromURL(String url){ String content = readStringFromURL(url); return new Document(content); } public static Document fromFile(String filename){ String content = readFile(filename); return new Document(content); }

Maintenant, nous allons créer une classe SearchEngine qui implémentera un moteur de recherche de documents. Pour l'instant, on veut pouvoir instancier un moteur de recherche, lui rajouter des documents et pouvoir, à partir d'un terme, obtenir la liste des documents contenant ce terme. Pour cela, considérez qu'il est trop long de parcourir la liste des documents.

Une méthode capable de donner rapidement les documents contenant un terme donné s'appelle un index inversé.

En pratique:

Créer un champ HashMap<String, ArrayList<Document>> inverseIndex
Implémentez une méthode void add(Document document)

Attention toutefois de ne pas rajouter plusieurs fois un document pour un mot donné !

SearchEngine0.java

Nous pouvons maintenant calculer la deuxième moitié de TFIDF, IDF. IDF signifie inverse document frequency et est donné par la formule suivante:

idf(mot) = log(\frac{\text{Nombre total de documents}}{\text{Nombre de documents contenant mot}})

L'idée dernière cette formule est que plus un mot apparait dans beaucoup de documents, moins il est important dans la recherche.
Écrivez une fonction pour obtenir l'IDF d'un mot (double getIDF(String word)), puis une fonction pour obtenir le TFIDF d'un mot et d'un document (double getTFIDF(String word, Document document)). Le TFIDF est simplement le produit de la TF et de l'IDF:

tfidf(mot, document) = tf(mot, document) * idf(mot)

TFIDF.java

Nous allons bientôt pouvoir faire notre recherche. Avant cela, il nous faut pré-traiter notre requête. Une requête peut être représentée par un document. On veut qu'à la fin du prétraitement, on ait un tableau de mots tous différents obtenus à partir de la requête et tels que l'IDF de chaque mot soit supérieur à un seuil donné (1e-4 par exemple). Cela nous permettra d'éliminer les mots trop fréquents.
Par exemple, "the peter pan and peter" deviendra "peter pan" car "peter" apparait deux fois et "the" et "and" sont trop populaires.
Écrivez cette méthode de prétraitement String[] getWordsQuery(Document query).

private String[] getWordsQuery(Document query){ String[] words = query.preprocess(); HashSet<String> uniqueWords = new HashSet<>(); for (int i = 0; i < words.length; i++){ if (this.getIDF(words[i]) > 1e-4){ uniqueWords.add(words[i]); } } String[] uniqueWordsArray = uniqueWords.toArray(new String[uniqueWords.size()]); Arrays.sort(uniqueWordsArray); return uniqueWordsArray; }

Écrivez une méthode search permettant d'obtenir le document le plus pertinent pour une requête donnée. Pour cela, il faudra:

Récupérer la liste des documents potentiels (c'est-à-dire contenants au moins un mot de la requête pré-traitée)
Calculer un score pour chacun de ces documents. Pour faire simple, nous définissons le score comme étant la somme des TFIDF des mots de la requête (pré-traitée).
Prendre le meilleur document.

On pourra tester le code avec les documents suivants obtenus sur le site du Projet Gutenberg :

            Document[] documents = {
                Document.fromURL("https://www.gutenberg.org/files/16/16-0.txt"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/1513/pg1513.txt"),
                Document.fromURL("https://www.gutenberg.org/files/2701/2701-0.txt"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/2641/pg2641.txt"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/145/pg145.txt"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/37106/pg37106.txt"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/67979/pg67979.txt"),
                Document.fromURL("https://www.gutenberg.org/ebooks/16389"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/6761/pg6761.txt"),
                Document.fromURL("https://www.gutenberg.org/cache/epub/394/pg394.txt"),
                Document.fromURL("https://www.gutenberg.org/files/2160/2160-0.txt"),
                Document.fromURL("https://www.gutenberg.org/files/4085/4085-0.txt"),
                Document.fromURL("https://www.gutenberg.org/ebooks/1342"),
                Document.fromURL("https://www.gutenberg.org/ebooks/6593")
            };
        

Quel livre correspond à la requête ""pirate island" ?

Search.java

Document.java

SearchEngine.java

Mise en pratique des sets et maps (entraînement)

Les questions dans cet exercice sont indépendantes. Ils demandent d'une manière ou d'une autre d'utiliser un set ou une table d'association. Vous pouvez utiliser votre implémentation ou directement celle donnée dans Java, aussi appelés HashSet et HashMap.

Soit T un tableau d'entiers et S un entier. Écrivez un algorithme de complexité linéaire trouvant deux entier a et b dans T tels quels que a + b = S.

Vous ne pouvez pas utiliser une double boucle !

Utilisez un HashMap pour construire un index inversé, c'est-à-dire qui soit l'inverse d'un tableau : il associe à chaque élément son indice dans le tableau.

SumTwo.java