CI6 : Un petit interpreteur
Cet exercice a pour objectif de travailler sur l'héritage et les interfaces, et de vous faire découvrir les principes permettant d'écrire un petit interpréteur, c'est-à-dire un programme capable d'exécuter d'autres programmes.
Durée des exercices obligatoires : 2h en présentiel
- Exercice 1 : obligatoire (facile, ∼20mn)
- Exercice 2 : obligatoire (moyen, ∼30mn)
- Exercice 3 : obligatoire (difficile, ∼40mn)
- Exercice 4 : obligatoire (difficile, ∼30mn)
- Exercice 5 : entraînement (moyen, ∼1h)
- Exercice 6 : entraînement (difficile)
Écrire un interpréteur complet capable de lire un autre programme source et de l'interpréter étant un peu trop long à réaliser dans le cadre d'un TP, nous ne nous préoccupons que de la partie interprétation à partir d'un arbre de syntaxe abstrait. Un arbre de syntaxe abstrait est une représentation sous forme d'arbre d'un programme. Dans notre cas, un arbre est constitué de nœuds qui peuvent correspondre à des opérations (addition, soustraction etc.), des variables ou des scalaires (des entiers).
Par exemple, l'arbre représenté ci-dessous correspond à l'expression x = x + 42 en Java. La racine de l'arbre est une opération d'affectation qui affecte la partie droite de l'arbre (l'expression qui ajoute 42 à la variable x) à la partie gauche (la variable x).
Dans l'exercice, nous aurons besoin de représenter des arbres sous une forme textuelle. Pour cela, nous affichons un arbre sous une forme préfixée et parenthésée : chaque nœud de l'arbre qui représente une opération est affiché sous la forme (op e1 ... en), où op est l'opération et e1 ... en les paramètres. Typiquement, nous afficherons l'arbre ci-dessus sous la forme (set! x (+ x 42)) : set! représente une opération d'affectation, le premier x l'élément de gauche et (+ x 42) l'élément de droite (puisque l'opération est une addition avec comme paramètres x et 42). Les étudiants fins connaisseurs remarqueront que cette écriture est celle du langage Scheme.
Un simple additionneur (∼20mn – facile – obligatoire)
Nous commençons par mettre en œuvre un simple additionneur, c'est-à-dire une classe capable d'additionner deux scalaires.
- public int get() : cette méthode renvoie la valeur du scalaire,
- public String toString() : cette méthode retourne une chaîne de caractères représentant la valeur du scalaire en utilisant la méthode statique Integer.toString(int i).
- public int execute() : renvoie le résultat de l'addition de l'opérande de gauche avec l'opérande de droite.
- public String toString() : renvoie la chaîne de caractères (+ e1 e2), dans laquelle e1 est la représentation de left sous la forme d'une chaîne de caractères et e2 celle de right.
Additions imbriquées (∼30mn – moyen – obligatoire)
Nous souhaitons maintenant rendre notre additionneur générique dans le sens où les opérandes de gauche et de droite doivent pouvoir être des scalaires ou elles-mêmes des opérations d'addition. De cette façon, nous pourrons évaluer une expression comme (+ (+ 1 2) (+ 3 4)) qui devrait donner comme résultat 10. Pour cela, nous créons une interface générique nommée Node représentant un nœud quelconque de l'arbre, c'est-à-dire un scalaire ou un additionneur. La figure ci-dessous présente l'arbre d'héritage/mise en œuvre que nous utilisons :
Techniquement, l'interface Node doit définir une unique méthode nommée int execute() qui va permettre d'évaluer un nœud. Si le nœud est un scalaire, le résultat de son évaluation est sa valeur. Si le nœud est un additionneur, le résultat de son évaluation est la somme du résultat de l'évaluation du membre de gauche avec celle du membre de droite.
Calculette multi-opérations (∼40mn – difficile – obligatoire)
Nous souhaitons maintenant ajouter de nouvelles opérations comme la multiplication de deux entiers ou l'inversion du signe d'un entier. Une première approche simple permettant d'ajouter ces opérations serait de créer des classes sur le modèle de Add mettant en œuvre Node, et effectuant l'opération. Toutefois, comme beaucoup de code serait alors redondant entre ces classes et la classe Add, nous préférons utiliser l'héritage pour factoriser un maximum le code. Tout au long de cet exercice, l'affichage produit par votre programme ne devrait pas varier par rapport à l'affichage que vous avez eu à la question précédente.
Nous modifions notre code étape par étape pour introduire une nouvelle classe générique représentant n'importe quelle opération. Dans un premier temps, nous insérons une classe abstraite nommée Operation dans l'arbre d'héritage. Cette classe représente une opération quelconque. Pour le moment, cette classe est vide, le but de la question n'étant que de l'insérer de façon à obtenir l'arbre d'héritage/mise en œuvre suivant :
Créez donc une classe abstraite nommée Operation et mettant en œuvre Node. Cette classe est abstraite, car elle ne met pas elle-même en œuvre la méthode execute qui est mise en œuvre dans les classes filles. Modifiez ensuite la classe Add de façon à ce qu'elle ne mette plus en œuvre Node, mais hérite de Operation.
- un champ privé Node[] ops contenant l'ensemble des opérandes,
- une méthode publique Node op(int i) permettant d'accéder à la iième opérande,
- une méthode publique int nbOps() renvoyant le nombre d'opérandes,
- un constructeur publique Operation(Node... ops) permettant d'initialiser le champ ops de Operation. On vous rappelle que Node... ops permet de déclarer une méthode avec un nombre variable d'arguments, et que les arguments sont rangés sous la forme d'un tableau dans ops.
Écrivez une classe Neg héritant de Operation et permettant d'inverser le signe de son opérande. Modifiez la méthode main de façon à afficher et évaluer l'arbre (+ (+ 1 2) (- (+ 3 4))) qui devrait donner comme résultat -4.
À cette étape, l'arbre d'héritage que vous devriez avoir est le suivant :
Les variables (∼30mn – difficile – obligatoire)
Nous souhaitons maintenant ajouter des variables à notre langage. Vous remarquerez qu'une variable est simplement un scalaire possédant un nom. Pour cette raison, nous réutilisons la classe Scalar pour mettre en œuvre les variables.
- un champ String name indiquant le nom de la variable,
- un constructeur prenant en argument le nom de la variable et pré-initialisant la variable à 0 en utilisant super.
L'arbre d'héritage que vous devriez avoir à cette étape est le suivant :
L'exécution d'une opération Set doit :
- évaluer le membre de droite de l'opération,
- affecter le résultat de cette évaluation à la variable (membre de gauche),
- renvoyer ce résultat.
La méthode op(0) renvoie la variable, mais cette dernière a le type Node, ce qui fait que vous ne pouvez pas directement invoquer le set(int value) de Variable pour modifier la valeur de la variable. Pensez que vous pouvez transtyper explicitement un Node en Variable puisque vous manipulez bien un objet de type Variable.
L'arbre d'héritage que vous devriez avoir à cette étape est le suivant :
Vers un interpréteur complet (∼1h – moyen – entraînement)
Vous pouvez maintenant compléter votre petit interpréteur d'arbre pour lui ajouter quelques fioritures comme des structures de contrôle.
Arbre Couvrant Minimal (entraînement)
Dans cet exercice, nous continuons notre travail sur les graphes entamé lors du CI4, et nous allons travailler sur le même exemple. Notre but est d'implémenter un algorithme pour obtenir un arbre couvrant minimal d'un graphe. Un arbre couvrant d'un graphe est un arbre dont les nœuds sont les mêmes que le graphe et dont les arêtes sont incluses dans celles du graphe. Comme c'est un arbre, il n'utilisera pas toutes les arêtes. De plus, il est dit minimal si c'est l'arbre couvrant tel que la somme des poids des arêtes soit minimale.
Pour la représentation textuelle, il faudra réimplémenter toString venant d'Object.
On pourra utiliser une fonction auxiliaire récursive. Pour savoir si un nœud a déjà été visité ou pas, on peut rajouter un champ privé visited. Cependant, il ne faut pas oublier de le réinitialiser avant de terminer la fonction !
Nous commencerons toujours par graph{ et terminerons par }. Ensuite, chaque ligne représente une arête. Nous mettons à gauche et à droite de deux tirets le représentant du nœud, qui est ici son nom avec les espaces remplacés par des _ (on peut utiliser la fonction s.replace). Au bout de la ligne, nous avons le label de l'arête qui est la distance entre les deux villes. Nous l'avons simplifiée ici pour la rendre plus lisible avec un Math.floor.
Écrivez une fonction pour obtenir la représentation sous le format dot d'un graphe.
Bien que vous puissiez utiliser une concaténation de String avec s1 + s2, cela peut se révéler inefficace en pratique. En effet, concaténer deux String revient à concaténer deux tableaux, et donc à recréer un nouveau tableau de taille suffisante et d'y copier les deux String. Cela nous donne rapidement des complexités quadratiques en le nombre de concaténations. À la place, vous pouvez utiliser un StringBuilder.
Une fois la fonction implémentée, vous pouvez visualiser votre graphe en ligne en visitant ce site : https://dreampuf.github.io/GraphvizOnline.
Vous aurez sûrement besoin de la liste des arêtes...
Faites en sorte que Edge soit de type Comparable<Edge>. On devra rajouter dans la définition de la classe class Edge implements Comparable<Edge>
- Chaque Location se voit attribuer un indice unique qui va correspondre à une position dans un tableau.
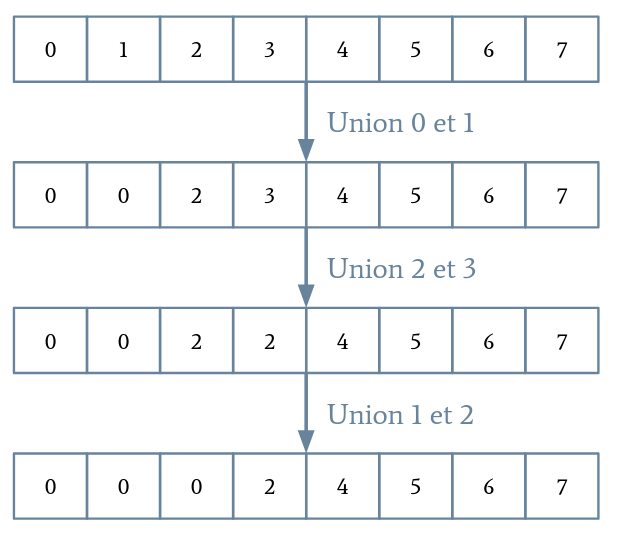
- Un champ parents contiendra pour chaque indice son indice parent. Au début, chaque élément est son propre parent.
- Un représentant d'un set est un indice qui est son propre parent. Pour savoir dans quel set appartient un indice, nous devons remonter ses parents jusqu'à trouver un représentant.
- Pour faire l'union de deux sets à partir de deux indices donnés, on commence par prendre les deux représentants. Ensuite, on définit le parent de l'un comme étant le parent de l'autre.
Cet algorithme s'appelle Union-Find.
Sachez que cette complexité peut devenir logarithmique avec une implémentation à base d'arbres.
Implémentez cet algorithme. Notez qu'il ne renvoie pas un arbre à proprement parler, mais que l'on pourrait facilement le créer à partir des arêtes.
On peut extraire une méthode statique de la fonction implémentée plus haut et fonctionnant avec une ArrayList de Edge.

