CI3 : L'armée de monstres
- Exercice 1 : obligatoire (facile, ∼40mn)
- Exercice 2 : obligatoire (moyen, ∼1h)
- Exercice 3 : obligatoire (facile, ∼15mn)
- Exercice 4 : entraînement (difficile, ∼45mn)
- Exercice 5 : entraînement (difficile)
- Dans une première partie, nous concevons la structure de données qui représente un monstre.
- Dans une seconde partie, nous utilisons des tableaux extensibles pour stocker nos monstres. Un tableau extensible est une structure de données reposant sur un tableau, mais permettant de réallouer dynamiquement le tableau de façon à l'étendre. Dans cette partie, ainsi que dans la précédente, nous concevons notre application de manière non modulaire, c'est-à-dire que nous mettons en vrac l'ensemble des méthodes de notre programme dans la même classe.
- Dans une troisième partie, nous constatons que cette conception non modulaire ne permet pas de réutiliser le code. Pour cette raison, nous modifions le design de notre application.
- Dans une quatrième partie, nous observons qu'un tableau extensible n'est pas la structure de données la plus efficace en termes de performance si le nombre de monstres devient grand. Pour cette raison, nous modifions notre application de façon à utiliser des listes chaînées pour stocker nos monstres.
Les monstres (∼45mn – facile – obligatoire)
- name : une chaîne de caractères donnant le nom du monstre.
- health : un entier donnant le nombre de points de vie du monstre. Lorsque ce nombre tombe à zéro, le monstre meurt.
On rappelle qu'il est possible de concaténer deux String avec un +.
Le tableau extensible (∼60mn – moyen – obligatoire)
Dans cette partie nous utilisons des tableaux extensibles pour stocker nos monstres. Dans un premier temps, avant de nous occuper de rendre nos tableaux extensibles, nous commençons par utiliser des tableaux à taille fixe.
Le principe, à cette étape, est d'allouer un tableau suffisamment grand pour accueillir nos 8 monstres, et d'utiliser un indice indiquant le niveau de remplissage du tableau. Initialement cet indice d'insertion vaut 0. L'ajout du premier monstre se fait donc à cet indice dans le tableau et l'indice d'insertion est augmenté de 1. De façon similaire, si l'indice d'insertion vaut N, l'ajout d'un nouveau monstre se fait dans la case d'indice N du tableau et l'indice d'insertion est ensuite augmenté de 1.

Au début de l'exercice, nous considérons que le tableau a toujours une taille suffisante pour accueillir un nouveau monstre, et nous ne nous préoccuperons de gérer le problème du débordement du tableau qu'à la fin de l'exercice.
Techniquement, displayArmy doit afficher les monstres se trouvant aux indices allant de 0 (inclus) à top (non inclus) du tableau monsters.

- Allouer un nouveau tableau nommé tmp. Ce tableau doit avoir une taille plus grande que le tableau de monstres original (par exemple, en doublant la taille du tableau original).
- Recopier le tableau original de monstres dans le tableau tmp.
- Affecter tmp au champ monsters de l'armée.
Dans le meilleur des cas, il n'y a presque rien à faire : la complexité est constante.
Conception modulaire (∼15mn – facile – obligatoire – exercice très important !)
Face au succès phénoménal de votre jeu, votre PDG, toujours aussi visionnaire, souhaite lancer une nouvelle franchise basée sur le film Black Sheep relatant les passionnantes aventures de moutons zombies. Dans ce nouveau jeu, un joueur se promène dans le monde réel et rencontre des moutons zombies géolocalisés qui se mettent à l'attaquer. Le joueur doit collectionner des pieux en argent pour vaincre les moutons zombies, ce qui lui rapporte des pièces lui permettant d'acheter des vêtements de luxe, le but du jeu étant d'avoir le personnage le plus chic du monde.
La liste chaînée (∼45mn – difficile – entraînement)
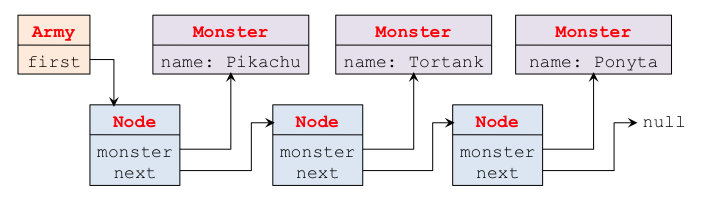
Si vous utilisez IntelliJ, vous pouvez maintenant ouvrir le projet copié en allant dans File, Open et en sélectionnant votre nouveau dossier de projet. Une fois le projet ouvert, cliquez sur le bouton de droite sur le dossier du projet dans l'interface d'IntelliJ, puis Refractor et Rename. Mettez le nouveau nom (monster-array par exemple). Suite à l'extraordinaire succès de votre jeu, vous vous mettez à recevoir des centaines de milliers de mails d'utilisateurs mécontents, car les performances de votre jeu sont désastreuses. Après une analyse de performance poussée, vous vous apercevez que des joueurs monomaniaques collectionnent des centaines de milliers de monstres. Lorsque le tableau extensible est étendu pour accueillir les nouveaux monstres de ces joueurs, des centaines de milliers de cases sont copiées de l'ancien tableau vers le nouveau, ce qui écroule les performances de vos serveurs et impacte l'ensemble des joueurs connectés au même serveur (cette anecdote est bien sûr imaginaire, mais ressemble aux problèmes de performances que vous pouvez rencontrer tous les jours dans une entreprise). De façon à éviter ces recopies de tableaux, nous mettons en œuvre l'armée de monstres avec des listes chaînées. Une liste chaînée est une structure de données classique évitant cette recopie au prix d'un temps de parcours des éléments plus long. Le principe est de construire une chaîne d'éléments homogènes, chacun référençant le suivant de la liste. Pour cela, nous introduisons une nouvelle classe nommée Node permettant de référencer (i) une instance de Monster et (ii) l'instance de Node suivante dans la liste. La figure ci-après présente la structure sous une forme graphique. Chaque boite représente une instance d'une classe. Le nom en haut de la boite donne le nom de la classe instanciée et les noms en dessous sont les champs les plus importants de l'instance. Les flèches quant à elles représentent les références. Dans cette illustration, l'armée (l'instance de Army) référence le premier nœud de la liste chaînée. Le premier nœud référence un premier monstre (Pikachu) et le deuxième nœud. Le deuxième nœud référence le deuxième monstre (Tortank) et le nœud suivant de la liste, jusqu'à la fin de la liste qui est indiquée par la référence null.
Techniquement, il vous suffit d'appeler la méthode create de Node de façon adéquate et d'affecter le résultat de cet appel au champ first de l'armée.
Il faut initialiser le nouveau nœud avec comme argument (i) l'ancienne valeur de first et (ii) le nouveau monstre.
Pour afficher votre liste, il vous suffit d'utiliser une variable locale de type Node nommée cur. Ensuite, vous pouvez utiliser une boucle qui s'arrête lorsque cur vaut null et qui, à chaque pas de la boucle, avance d'un cran dans la liste.
Techniquement, à chaque pas de la boucle, il faut exécuter cur = cur.next.
bonus
- Si le premier nœud de la liste (first) vaut null, il n'y a rien à faire.
- Si le premier nœud de la liste référence un nœud qui référence le monstre passé en paramètre (l'opérateur == permet de savoir si deux références sont identiques), alors il faut affecter first à first.next.
- Sinon, votre méthode doit parcourir la liste de façon à identifier le prédécesseur du nœud qui référence le monstre passé en paramètre. Une fois identifié, si le prédécesseur est stocké dans une variable locale nommée pred, votre méthode doit affecter pred.next.next à pred.next de façon à sauter le nœud que vous souhaitez supprimer.
bonus
bonus
bonus
Pour un tableau extensible, la complexité est constante.
bonus
- add qui prend en entrée un Node et un Monster et retourne une liste commençant par le monstre et continuant vers l'ancienne liste.
- del qui prend en entrée un Node et un Monster et retourne une liste sans le monstre.
- get qui prend en entrée un Node et un index et retourne le monstre à l'index ou null si ce n'est pas possible.
- display qui doit afficher tous les éléments de la liste.
La liste chaînée est naturellement compatible avec les fonctions récursives.
Pour aller plus loin (Entraînement)
Pour rendre la lecture des listes plus claire, on affichera les listes chaînées sous la forme : 20 -> 12 -> 10 -> 7 -> 5. Pour cela, on pourra utiliser la fonction System.out.print qui ne rajoute pas de retour à la ligne à la fin de chaque ligne.
Exemple: {5, 7, 10, 12, 20} devient 5 -> 7 -> 10 -> 12 -> 20.
Exemple: 20 -> 12 -> 10 -> 7 -> 5 devient 5 -> 7 -> 10 -> 12 -> 20.
Exemple: 0 -> 0 -> 1 -> 2 -> 2 -> 3 -> 4 -> 4 devient 0 -> 1 -> 2 -> 3 -> 4.
Exemple: 3 -> 2 -> 1 + 2 -> 1 = 5 -> 3 -> 1
Il faut utiliser deux curseurs qui parcourent la liste, dont un qui se déplace deux fois plus vite.
- Node getLastNode(Node node) qui retourne le dernier nœud d'une liste.
- Node mergeSorted(Node first, Node second) qui fusionne deux listes triées en une nouvelle liste triée elle aussi.
- Node mergeSortAux(Node nodeFrom, Node nodeTo) qui prend le nœud au milieu entre nodeFrom et nodeTo, trie chaque demie-liste et fusionne le résultat.

