CSC 3101 – Algorithmique et langage de programmation

Introduction

Il est attendu que tous les étudiants fassent les exercices obligatoires : toute notion vue dans un exercice obligatoire peut faire l'objet d'un exercice en examen.

Quelques séries d'exercices obligatoires sont un peu longues et vont probablement nécessiter du travail en hors présentiel. Prenez le temps de terminer ces exercices, ils sont tous importants !

Les exercices d'entraînement ne sont, en revanche, pas obligatoires. Mais les faire est plaisant, car vous pourrez approfondir les sujets étudiés. Pour les étudiants les plus à l'aise, vous pourrez probablement réussir à terminer les exercices d'entraînement en présentiel. Profitez-en !

Les algorithmes que vous allez étudier dans la première séance vous sont sûrement connus. C'est bien le but recherché par l'équipe pédagogique : le but de ces séances n'est pas que vous appreniez de nouveaux algorithmes, mais que vous puissiez acquérir rapidement une bonne dextérité en programmation Java en mettant en œuvre des algorithmes que vous avez (probablement) déjà étudiés.

CI1 : Premiers pas et tableaux

Dans cette série d'exercices, vous commencez à acquérir les bases du langage Java et vous apprenez des algorithmes simples (calcul du plus petit diviseur et mise en œuvre d'une calculette simple) et de tri.

Durée des exercices obligatoires : 3h en présentiel

Exercice 1 : obligatoire (facile, ∼10mn)
Exercice 2 : obligatoire (facile, ∼30mn)
Exercice 3 ou 4 : obligatoire (facile, ∼30mn)
Exercice 5 : obligatoire (facile, ∼20mn)
Exercice 6 : obligatoire (moyen, ∼40mn)
Exercice 7 : obligatoire (moyen, ∼30mn)
Exercice 8 : obligatoire (moyen, ∼60mn)
Exercice 9 : obligatoire (moyen, ∼20mn)
Exercice 10 : obligatoire (moyen, ∼30mn)
Exercice 11 : obligatoire (moyen, ∼1h10)
Exercice 12 : entraînement (moyen, ∼1h15mn)
Exercice 13 : entraînement (moyen, ∼30mn)
Exercice 14 : entraînement (moyen, ∼30mn)
Exercice 15 : entraînement (ninja, ∼1h, pour les étudiants les plus aguerris qui veulent s'amuser)
Exercice 16 : entraînement (moyen, ∼1h)

Installation (∼10mn – facile – obligatoire)

Cet exercice a pour but de vous accompagner pour installer les logiciels de base nécessaires pour faire le module. Vous avez besoin de deux logiciels :

Un environnement de compilation et d'exécution Java, aussi appelé le jdk (Java Development Kit). Il faut choisir nécessairement une version de Java supérieure à la version 11.
Un environnement de développement. Vous pouvez choisir n'importe quel environnement de développement (Eclipse, IntelliJ, VSCode, CodeBlocks, Visual Studio, etc.) : il n'y a aucune adhérence particulière à un environnement particulier. Toutefois, l'équipe enseignante ayant l'habitude de Eclipse, nous vous guidons pas à pas pour utiliser cet environnement à cette séance.

Les machines de TP utilisent uniquement Eclipse.

Si vous avez un Linux (Ubuntu ou Debian)

La plupart d'entre vous devriez avoir un Linux récent avec Ubuntu ou Debian. Pour installer Java, il vous suffit de saisir la commande suivante dans un terminal :

$ sudo apt install default-jdk

Vous pouvez vérifier que Java est bien installé en saisissant la commande java -version qui devrait vous donner la version installée.

Si par hasard cette commande échoue, vous pouvez lister les versions que vous pouvez installer avec

apt search openjdk

Il vous suffit alors de choisir une version quelconque du jdk (suffixe -jdk) supérieure à 11, par exemple : sudo apt install openjdk-11-jdk.

Pour installer Eclipse, la meilleure méthode est de suivre la procédure décrite ici. Il faut installer la version Eclipse IDE for Java Developers. Si par hasard vous bloquez quelque part et que vous avez une Ubuntu, vous pouvez aussi saisir la commande suivante :

sudo apt-get install -y snapd && sudo snap install --classic eclipse

Si vous avez un MacOS

Avec MacOS, il vous suffit d'installer Java à partir d'ici. Il faut sélectionner macOS. Ensuite, si vous avez un Apple M1, il faut sélectionner le dmg installer pour processeur Arm, et si vous avez un Apple Intel, il faut sélectionner le dmg installer pour processeur x64. Une fois Java installé, si vous lancez la commande java -version dans un terminal, vous devriez voir la version que vous avez installée.

Pour Eclipse, il vous suffit de le télécharger à partir d'ici. Pour Eclipse, il n'existe actuellement que la version x64. Si vous avez un Apple M1, la procédure d'installation va vous proposer d'installer Rosetta 2 qui permet d'émuler un processeur Intel sur votre ARM, ce qu'il faut autoriser. Pour Eclipse, il faut installer la version Eclipse IDE for Java Developers.

Vous pouvez manuellement installer Roseta 2 avec la commande suivante : softwareupdate --install-rosetta dans un terminal.

Si par hasard vous avez un MacOS assez ancien (plusieurs années) et que la dernière version de Java ne fonctionne pas, il faut installer une ancienne version. Vous pouvez alors vous rabattre sur une version 11 de Java que vous trouverez ici, ou même une version 8 encore plus ancienne que vous trouverez ici.

Si vous avez un Windows

Si vous avez un Linux et un Windows, nous vous conseillons vivement d'utiliser Linux, car l'équipe enseignante étant beaucoup moins à l'aise avec Windows ne pourra que difficilement vous dépanner. Toutefois, si vous n'arrivez pas à avoir un Linux fonctionnel avec le réseau et les connexions aux salles de cours en même temps que Java/Eclipse, vous pouvez vous rabattre vers la procédure qui se trouve à cette adresse.

Cette procédure est aussi beaucoup plus complexe car Windows est, contrairement à l'intuition, un système plus difficile à administrer que Linux ou MacOS.

Si vous avez un autre système

Si vous avez du mal avec votre système, n'hésitez pas à demander à vos professeurs qui pourront essayer de vous aider s'ils connaissent ce système (archlinux, gentoo, OpenBSD, etc.).

Mise en route (∼30mn – facile – obligatoire)

Le but de cet exercice est de vous faire utiliser explicitement toute la chaîne de conception, compilation et exécution de Java. Si jamais vous utilisez Windows ou que vous n'avez pas Java installé sur votre machine, vous pouvez utiliser les machines de l'école pour cet exercice. Par la suite, nous utiliserons un IDE qui gèrera pour nous Java.

Dans cet exercice, on vous demande de ne pas utiliser une interface de développement avancée comme eclipse.

Créez un répertoire csc3101 et placez-vous dans ce répertoire. Ouvrez ensuite un terminal et lancez un éditeur de texte simple pour éditer le fichier HelloWorld.java. Par éditeur de texte simple, nous entendons emacs, gedit, vi ou tout autre éditeur que vous avez apprécié utiliser en CSC3102 (Introduction aux systèmes d'exploitation).

Écrivez un programme affichant Bonjour, monde !!!. Compilez ce programme avec javac puis exécutez-le avec java.

HelloWorld.java

$ emacs HelloWorld.java
$ javac HelloWorld.java 
$ java HelloWorld
Bonjour, monde !!!
$

Déplacez-vous dans votre répertoire racine et lancez java csc3101/HelloWorld. Que constatez-vous ?

Techniquement, l'interpréteur java est incapable de lancer un programme Java à partir de son chemin. Pour lancer un programme Java à partir d'un autre répertoire, il faut utiliser la variable d'environnement CLASSPATH, qui contient un ensemble de chemins séparés par des deux points (:). Lancez la commande suivante : CLASSPATH=~/csc3101 java HelloWorld. Que constatez-vous ?

Après être revenu dans le répertoire csc3101, modifiez votre programme de façon à afficher chacun des arguments sur une ligne séparée. Votre programme devrait générer la sortie suivante :

$ java HelloWorld Ah que coucou
Bonjour, monde !!!
args[0]: Ah
args[1]: que
args[2]: coucou
$

HelloWorld.java

Prise en main d'IntelliJ (∼30mn – facile – obligatoire/facultatif)

Cet exercice ou le suivant est obligatoire. Toutefois, pour avoir le même environnement de travail que les salles de TP, nous recommandons de quand même le faire (hors présentiel).

Dans ce cours, nous vous demandons d'utiliser un environnement de développement Java adéquat, par exemple eclipse ou intellij. En particulier, nous vous déconseillons fortement l'utilisation d'un éditeur de texte simple comme gedit : en utilisant un environnement de développement efficace, vous verrez rapidement que votre productivité sera améliorée.

Ce cours s'adresse à ceux ayant installé IntelliJ. Si vous voulez l'installer, suivez le tutoriel sur le site officiel qui vous fait installer la Toolbox App. Ensuite, vous pouvez installer soit la version gratuite (Community Edition), soit la version payante qui est gratuite pour les étudiants (il faut s'inscrire ici).

Pour lancer IntelliJ, vous pouvez utiliser idea &. Si cette commande ne marche pas (votre variable PATH est peut-être mal configurée) vous pouvez le chercher dans la liste des applications ou à travers la Toolbox.

Vous pouvez maintenant créer un premier projet Java. Si c'est la première fois que vous ouvrez IntelliJ, vous devriez trouver un bouton pour créer un nouveau projet. Sinon, allez dans le menu File->New->Project. Donnez le nom bonjour à votre projet. Définissez le dossier où votre projet sera enregistré. Le langage est Java et le Build System est IntelliJ. Enfin, il y a une dernière option à remplir : la JDK. Si Java est déjà installé sur votre machine, un numéro de version devrait apparaître. Sinon, cliquez sur la case de sélection puis Download JDK. Sélectionnez la version 20, et ensuite cliquez sur Download. Une fois le téléchargement terminé, revenez sur la fenêtre de création de projet. Un numéro de JDK devrait apparaitre. Sinon, sélectionnez le manuellement. Finalement, cliquez sur Create.

À gauche de votre écran, vous pouvez voir votre projet avec la liste des fichiers qu'il contient. En particulier, vous trouverez un répertoire src dans lequel seront stockés les fichiers sources Java de votre programme, un dossier .idea qui contient les configurations d'IntelliJ, ainsi qu'un ensemble de fichiers constituant la bibliothèque standard Java (JRE System Library).

Vous pouvez maintenant créer votre première classe. Pour cela, sélectionnez le menu File->New->Java Class ou click droit sur le dossier src et New->Java Class.

Dans la fenêtre qui vient de s'ouvrir, donnez le nom Bonjour à votre classe dans le champ Name.

Comme vous aurez besoin d'ajouter un main dans notre classe, vous pouvez demander à IntelliJ de générer pour vous le code public static void main(String[] args) { ... } qui est bien fastidieux à écrire. Pour cela, il vous suffit de taper main dans la classe et IntelliJ vous proposera de compléter le code pour vous !

À présent que la classe est générée, dans la vue centrale de l'écran (l'éditeur de code), vous devriez voir apparaître le contenu du fichier Bonjour

Nous allons maintenant écrire la méthode main de notre programme. Dans un premier temps, votre programme doit simplement afficher Bonjour, monde !!!.

Quand vous tapez du code sur IntelliJ, il vous proposera de compléter ce que vous écrivez. Vous pouvez rapidement choisir l'option qui vous convient dans le menu déroulant. Par exemple, si vous saisissez System.out.pr, vous devriez voir toutes les possibilités de complétion avec les types associés. IntelliJ possède aussi de nombreux raccourcis. Par exemple, si vous tapez sout, IntelliJ comprend que vous voulez écrire System.out.println qui est beaucoup plus long. Usez et abusez de cette possibilité dès que vous avez besoin d'écrire un symbole qu'IntelliJ a déjà rencontré (y compris des noms de variables locales), vous gagnerez beaucoup de temps !

Nous allons désormais tester notre programme, c'est-à-dire que nous allons le compiler en bytecode puis l'exécuter. Pour tester votre programme, vous devriez remarquer un petit bouton vert avec le signe lecture en haut de votre fenêtre. Un bouton vert similaire s'affiche également à gauche de la fonction main et à gauche du nom de la classe si cette classe contient une fonction main

Si vous cliquez sur ce bouton, le programme se lance et vous affiche le résultat dans la vue Console qui s'ouvre par défaut en bas de l'écran. Bravo, vous avez à présent pris en main IntelliJ !!!

Comme dans l'exercice précédent, nous souhaitons maintenant afficher les paramètres du programme. Modifiez votre programme en conséquence.

Pour spécifier des paramètres, vous devez aller dans le menu Run->Edit Configurations. Dans Program Arguments, vous pouvez spécifier des arguments. Utilisez les arguments suivants : Que la force soit avec toi. Vérifiez, en utilisant le bouton run, que votre programme affiche bien ces paramètres.

Bonjour.java

Comme modifier les paramètres avec la procédure que nous venons de vous expliquer est long et fastidieux, vous avez le moyen de spécifier que vous voulez systématiquement interroger l'utilisateur pour qu'il saisisse les paramètres au moment du lancement de l'application. Pour cela, il suffit de revenir dans Run->Edit Configurations (voir question précédente) et de remplacer le Que la force soit avec toi par $Prompt$. Vérifiez que vous arrivez bien à saisir des paramètres à chaque fois que vous lancez votre application avec cette procédure.

Prise en main de eclipse (∼30mn – facile – obligatoire/recommandé)

Non obligatoire si vous avez installé IntelliJ. Nous vous guidons pas à pas pour utiliser eclipse dans ce TP.

Lancez eclipse. Si vous êtes sur votre propre machine ou sur les machines de TP, il suffit de saisir eclipse & dans le terminal. Sur les machines de TP, si vous lancez Eclipse depuis les menus, vous devez utiliser eclipse-java.

Vous remarquerez que eclipse vous demande de sélectionner votre workspace, c'est-à-dire votre espace de travail. Ce répertoire de travail est la racine à partir de laquelle eclipse enregistre vos projets. Vous pouvez laisser le répertoire par défaut, mais vous pouvez aussi sélectionner le répertoire ~/csc3101 que vous avez créé dans l'exercice précédent (votre programme HelloWorld.java n'apparaîtra probablement pas, c'est normal).

Une fois Eclipse lancé, il est possible, sur d'ancienne version, qu'il faille sélectionner Workbench dans la fenêtre principale.

Eclipse définit une notion de perspective : une perspective est une façon de vous présenter votre espace de travail.

Par défaut, eclipse ouvre la perspective Java qui vous présente votre espace de travail comme un ensemble de projets Java. Vous pouvez changer de perspective à tout moment via le menu Window->Perspective->Open Perspective, mais vous ne devriez pas avoir besoin de cette fonctionnalité pour le moment.

Vous pouvez maintenant créer un premier projet Java. Allez dans le menu File->New->Project. Dans le sous menu Java, sélectionnez Java Project. Donnez le nom bonjour à votre projet.

Une perspective est constituée de vues, c'est-à-dire de sous-fenêtres. Vous pouvez ajouter des vues via le menu Window->Show View, mais vous ne devriez pas encore avoir besoin de cette fonctionnalité à cette étape.

Dans la vue Package Explorer se trouvant normalement à gauche de votre écran, vous pouvez voir vos projets. Vous avez désormais un unique projet appelé bonjour. Si vous cliquez sur ce projet, vous pouvez observer le contenu de ce projet : un répertoire src dans lequel seront stockés les fichiers sources Java de votre programme, ainsi qu'un ensemble de fichiers constituant la bibliothèque standard Java (JRE System Library). Pour les utilisateurs d'un environnement Java récent, vous aurez aussi un fichier nommé module-info.java. Cette notion de module vous sera brièvement présentée au dernier TP. Pour le moment, laissez ce fichier qui est nécessaire au bon fonctionnement des programmes Java sans y toucher.

Vous pouvez maintenant créer votre première classe. Pour cela, sélectionnez le menu File->New->Class.

Ne cliquer sur Finish qu'une fois que vous avez intégralement lu la question !

Dans la fenêtre qui vient de s'ouvrir, donnez le nom Bonjour à votre classe dans le champ Name. Ensuite, il faut s'assurer que votre fichier source va être bien rangé. Java range les classes dans des packages. Nous reviendrons sur cette notion en CI4, mais à haut niveau, les packages sont des sortes de répertoires dans lesquelles on range les fichiers sources d'un programme. Il faut savoir que tout fichier source doit être rangé dans un package, et qu'il ne faut pas utiliser le package racine (appelé default). Assurez-vous donc que dans le champ Package (un peu au-dessus du champ Name qui donne un nom à votre classe), vous avez bien un nom. Si c'est déjà le cas, gardez le nom qu'Eclipse a choisi pour vous. Si ce n'est pas le cas, donnez le nom bonjour à votre package (vous pouvez choisir n'importe quel nom).

Comme vous aurez besoin d'ajouter un main dans notre classe, vous pouvez demander à Eclipse de générer pour vous le code public static void main(String[] args) { ... } qui est bien fastidieux à écrire. Pour cela, il vous suffit, en bas de la fenêtre, de cliquer sur public static void main(Strings[] args) à la question Which method stubs would you like to create. Laissez systématiquement le Inherited abstract methods. Vous comprendrez l'intérêt de cette fonctionnalité au CI6.

Vous pouvez maintenant cliquer sur Finish pour générer votre première classe.

Comme nous ne vous le rappellerons plus dans la suite, à chaque fois que vous créez une classe, pensez à vous assurer vous qu'elle soit bien rangée dans un package : si vous placez une classe dans le package par défaut, vous aurez des erreurs.

À présent que la classe est générée, dans la vue centrale de l'écran (l'éditeur de code), vous devriez voir apparaître le contenu du fichier Bonjour Vous remarquerez que, comparé au cours, eclipse vous a ajouté une ligne contenant package au début du fichier et le mot clé public devant le mot clé class. Comme expliqué plus haut, la notion de package vous sera expliquée en CI4 et il faut laisser cette ligne. La notion de public vous sera aussi présentée en CI5, vous pouvez laisser la déclaration telle qu'elle est.

Nous allons maintenant écrire la méthode main de notre programme. Dans un premier temps, votre programme doit simplement afficher Bonjour, monde !!!.

Si vous tapez Control + (barre d'espace) sur un symbole en cours d'écriture, Eclipse vous propose les différentes complétions possibles. Par exemple, si vous saisissez System.out.pr et tapez Control + Espace, Eclipse va vous proposer de compléter avec println. Usez et abusez de cette possibilité dès que vous avez besoin d'écrire un symbole qu'Eclipse a déjà rencontré (y compris des noms de variables locales), vous gagnerez beaucoup de temps !

Nous allons désormais tester notre programme, c'est-à-dire que nous allons le compiler en bytecode puis l'exécuter. Pour tester votre programme, vous devriez remarquer un petit bouton vert avec le signe lecture en haut de votre fenêtre, comme celui entouré en rouge dans la figure ci-dessous :

Si vous cliquez sur ce bouton, le programme se lance et vous affiche le résultat dans la vue Console qui s'ouvre par défaut en bas de l'écran. Bravo, vous avez à présent pris en main eclipse !!!

Comme dans l'exercice précédent, nous souhaitons maintenant afficher les paramètres du programme. Modifiez votre programme en conséquence. Vous pourrez remarquer que, avec Eclipse, si vous tapez quelques lettres et que vous saisissez la combinaison de touches Contrôle + Espace, Eclipse vous propose gentiment de compléter votre code pour vous. Usez et abusez de cette possibilité !

Pour spécifier des paramètres, vous devez aller dans le menu Run->Run Configurations. Dans l'onglet (x)=Arguments, vous pouvez spécifier des arguments dans la fenêtre Program arguments. Utilisez les arguments suivants : Que la force soit avec toi. Vérifiez, en utilisant le bouton run, que votre programme affiche bien ces paramètres.

Bonjour.java

Comme modifier les paramètres avec la procédure que nous venons de vous expliquer est long et fastidieux, vous avez le moyen de spécifier que vous voulez systématiquement interroger l'utilisateur pour qu'il saisisse les paramètres au moment du lancement de l'application. Pour cela, il suffit de revenir dans l'onglet (x)=Arguments du menu Run->Run Configurations (voir question précédente) et de remplacer le Que la force soit avec toi par ${string_prompt}. Vérifiez que vous arrivez bien à saisir des paramètres à chaque fois que vous lancez votre application avec cette procédure.

Les types de base (∼20mn – facile – obligatoire)

Cet exercice a pour but de vous familiariser avec les types de base de Java et avec les conversions de types.

Créez un projet types avec une classe nommée Type contenant la méthode main. Lorsque vous créez la classe Type, vous devriez remarquer que eclipse vous propose gentiment de générer la méthode main pour vous, profitez-en ! IntelliJ a des fonctionnalités similaires (voir plus haut).

Copiez-collez le code suivant dans la méthode main et expliquez la sortie que vous observez dans la console. Pour les heureux utilisateurs et utilisatrices de Linux, on vous rappelle que pour copier du texte, il suffit de le sélectionner avec la souris, et que pour coller du texte, il suffit de cliquer sur la touche du milieu (la molette) de la souris.

Expliquez la sortie générée par votre programme.

  int x = 5;
  int y = x / 3;
  double d = 5;
  double e = d / 3;
  double f = x / 3;
  int g = (int)e; /* type moins fort : conversion explicite nécessaire */
  char r = 'a';
  int s = r;
  int t = 98;
  char u = (char)t; /* type moins fort : conversion explicite nécessaire */
		    
  String s1 = "y vaut " + y;
  String s2 = "e vaut " + e;
  String s3 = "f vaut " + f;
  String s4 = "g vaut " + g;
  String s5 = "r vaut " + r;
  String s6 = "s vaut " + s;
  String s7 = "t vaut " + t;
  String s8 = "u vaut " + u;

  System.out.println(s1);
  System.out.println(s2);
  System.out.println(s3);
  System.out.println(s4);
  System.out.println(s5);
  System.out.println(s6);
  System.out.println(s7);
  System.out.println(s8);

Pour les chaînes de caractères, l'opérateur + correspond à la concaténation, car avant une opération, les opérandes sont convertis vers le type le plus fort, c'est-à-dire le type chaîne de caractère.

Pour y, comme les opérandes sont des entiers, le quotient est calculé dans l'ensemble des entiers.

Pour e, comme d est un flottant, l'entier 5 est d'abord converti en flottant (type le plus fort) avant d'effectuer l'opération. En revanche, pour f, les deux opérandes étant des entiers, le calcul est effectué en entier (résultat 2) puis converti en flottant. Finalement, pour g, la conversion explicite d'un flottant vers un entier (type moins fort) correspond à la troncature.

Pour r, le nombre représentant le caractère 'a' est 97. Pour u, 98 représente le caractère 'b'.

Calcul du plus grand commun diviseur (∼40mn – moyen – obligatoire)

Le but de cet exercice est d'écrire un programme permettant de calculer le plus grand commun diviseur (pgcd) de deux entiers.

Créez un projet nommé pgcd contenant une classe Pgcd, elle-même contenant une méthode main.

Affichez les arguments de votre programme après avoir spécifié que ses paramètres sont 243 576.

Modifiez votre programme de façon à vérifier que le nombre d'arguments est bien égal à 2. Si ce n'est pas le cas, votre programme doit afficher un message d'erreur et quitter à l'aide de la méthode System.exit(n), où n est le code de retour de votre programme. Si vous vous souvenez de votre cours d'introduction aux systèmes, vous devriez vous rappeler que toute valeur différente de 0 signifie que votre programme quitte avec une erreur. Vérifiez que votre programme se comporte correctement en modifiant les paramètres. Après vos tests, pensez à rétablir les arguments 243 et 576.

Les arguments sont donnés sous la forme de chaînes de caractères. Il faut donc les convertir en entier avant de pouvoir calculer leur plus grand commun diviseur. Pour cela, définissez deux variables entières nommées p et q, et utilisez Integer.parseInt(uneChaine) pour convertir la chaîne de caractères uneChaine en entier. Affichez les valeurs de p et q.

Un algorithme calculant le plus grand commun diviseur peut reposer sur la propriété suivante :

si p=0, alors pgcd(p ,q) = q,
si q=0, alors pgcd(p ,q) = p,
si p>q, alors pgcd(p ,q) = pgcd(p-q, q),
sinon : pgcd(p, q) = pgcd(p, q-p).

Mettez en œuvre un algorithme itératif (par opposition à récursif) utilisant cette propriété pour calculer le plus grand commun diviseur de p et q. Pour cela, utilisez une boucle while. Si vous obtenez pgcd(243, 576) = 9, vous avez gagné, bravo !

Pgcd.java

Estimez la complexité de cet algorithme de PGCD dans le pire des cas en fonction de n = p + q.

Pour répondre à cette question, nous devons estimer la complexité des étapes de l'algorithme. Ici, tout est en

O (1)

. Ensuite, il nous faut borner le nombre maximum de passages dans la boucle while en fonction de n. Étant donné que p et q décroissent strictement à chaque tour de boucle, le nombre maximum d'itérations est n. En particulier, ce nombre d'itérations est atteint pour p=n-1 et q=1.
La complexité finale est donc

O (n)

Il est possible d'implémenter un algorithme de PGCD plus efficace en remarquant que si p ≥ q, pgcd(p, q) = pgcd(q, p mod q). Implémenter cette variation du PGCD.

Pgcd2.java

(Difficile) Estimez la complexité de ce nouvel algorithme dans le pire des cas en fonction de n = p + q. Pour cela, nous montrerons la propriété suivante : Soit

(p_{i}, q_{i})

tel que

p_{i} \geq q_{i}

et i le nombre d'itérations dans la boucle (si vous n'avez pas utilisé une structure récursive) avec ces deux entrées. Alors, nous avons

q_{i} \geq F i b_{i}

avec Fib la suite de Fibonacci. On rappelle que

F i b_{i} \underset{i \to + \infty}{\sim} φ^{i}

. Vous pouvez commencer par estimer la complexité de

p g c d (F i b_{i + 1}, F i b_{i})

en fonction de i, puis la traduire en une complexité en

F i b_{i}

Pour calculer la complexité de

p g c d (F i b_{i + 1}, F i b_{i})

, nous calculons

F i b_{i + 1} \equiv F i b_{i} + F i b_{i - 1} \equiv F i b_{i - 1} [F i b_{i}]

. Nous observons qu'à chaque étape, nous descendons d'un élément dans la suite de Fibonacci. On a donc une complexité linéaire en i. Comme

F i b_{i} \underset{i \to + \infty}{\sim} φ^{i}

on obtient une complixité en

O (l o g (F i b_{i}))

quand i tend vers l'infini.
Ensuite, on peut prouver la propriété par induction.

Si i = 0, alors $b_1=0 \ge Fib_0$
Si i = 1, alors $b_2 \ge 1 = Fib_1$
Pour k ≥ 1 itérations, on a l'enchainement $(a_{k+1}, b_{k+1}) \rightarrow (a_{k}, b_{k}) \rightarrow (a_{k-1}, b_{k-1})$ . Par conséquent, $a_k = b_{k+1}, a_{k-1} = b_k, b_{k-1} \equiv a_k [b_k]$ . On a donc $a_k = q*b_k+b_{k-1}, q \ge 1$ et $b_{k+1} \ge b_k+b_{k-1} \ge Fib_{k-1} + Fib_{k-2} = Fib_{k}$ .

À partir de là, on a informellement pour i très grand :

b_i \ge \phi^i

et donc

i \le \frac{log(b_i)}{log(\phi)}

. On en déduit que la complexité est en

\mathcal{O}(log(n))

Notons que le pire des cas se produit quand les entrées sont deux nombres de Fibonacci consécutifs.

Ma première calculette (∼30mn – moyen – obligatoire)

Le but de cet exercice est de vous familiariser avec les tableaux en programmant une petite calculette capable d'effectuer des additions.

Créez un projet nommé calculette contenant une classe Calculette, elle-même contenant une méthode main.

Affichez les paramètres de votre programme après avoir spécifié que les paramètres sont 8 6 1 3 5 2.

Les paramètres sont donnés sous la forme d'un tableau de chaînes de caractères. Notre calculette doit additionner les valeurs numériques correspondant à ces paramètres, et doit donc commencer par convertir chaque chaîne de caractères en valeur entière. Pour commencer, créez une variable tab de type tableau d'entiers, et initialisez cette référence vers un tableau ayant autant d'éléments que le paramètre de la méthode main (args).

Complétez votre programme de façon à afficher les éléments du tableau tab. Votre programme devrait afficher 6 fois l'entier 0 puisque vous avez 6 arguments et parce qu'un tableau est toujours pré-initialisé avec des 0 en Java.

Avant d'afficher le tableau tab, utilisez une boucle pour stocker dans tab la conversion en entier de chacun des éléments du tableau de chaînes de caractères donné en paramètre (args). Pour convertir une chaîne de caractères en entier, utilisez la méthode Integer.parseInt(String s) qui renvoie le résultat de la conversion de la chaîne de caractères s en entier.

Après avoir affiché le tableau tab, calculez la somme des éléments du tableau tab, puis affichez le résultat. Si votre programme vous affiche 25, vous avez gagné, bravo !

Calculette.java

Palindromes et anacycliques (∼60mn – moyen – obligatoire)

Le but de cet exercice est de vous familiariser avec les méthodes de classes en travaillant sur des tableaux de caractères.

Créez un projet nommé palindrome contenant une classe Palindrome, elle-même contenant une méthode main.

Créez une variable words initialisé avec les tableaux de caractères suivants :

{ 'a', 'n', 'i', 'm', 'a', 'l' },
{ 'r', 'a', 'd', 'a', 'r' },
{ 'r', 'e', 's', 'u', 'm', 'a' },
{ 'r', 'e', 's', 's', 'a', 's', 's', 'e', 'r' },
{ 'r', 'e', 'l', 'a', 'c', 'e', 'r' },
{ 'k', 'a', 'y', 'a', 'k' },
{ 'v', 'i', 'v', 'e', ' ', 'J', 'a', 'v', 'a', ' ', '!' }

On vous rappelle que pour copier/coller sous Linux, il faut sélectionner à la souris la zone que vous souhaitez copier, puis cliquer sur le bouton du milieu de la souris pour coller.

Le tableau words est donc un tableau de (références vers des) tableaux de caractères, dont le type est naturellement char[][].

La déclaration et l'initialisation d'un tableau de tableau s'écrit :

char tab[][] = {
  { 'p', 'r', 'e', 'm', 'i', 'e', 'r' },
  { 's', 'e', 'c', 'o', 'n', 'd' },
  ...
};

Écrivez une méthode de classe nommée printWord(char[] word) affichant chacun des caractères du tableau de caractères word. De façon à éviter un retour à la ligne après l'affichage de chaque caractère, vous pouvez utiliser la méthode System.out.print(String msg) au lieu de la méthode System.out.println(String msg). Utilisez ensuite la méthode printWord pour afficher words[0] à partir de la méthode main.

Pour afficher un caractère, il suffit d'utiliser System.out.print(char c) (sans retour à la ligne) ou System.out.println(char c) (avec retour à la ligne). Notez que System.out.println(char c) est une surcharge de System.out.println(String msg) que vous avez déjà utilisé. Vous pouvez aussi utiliser System.out.println() sans paramètre, qui est une troisième surcharge et qui génère uniquement un retour à la ligne sans rien afficher de plus.

Pensez à utiliser la documentation Java (voir menu Liens utiles). Par exemple, vous pouvez voir les méthodes qui permettent d'effectuer des affichages dans le terminal ici.

Écrivez une méthode de classe nommée printWords(char[][] words) utilisant printWord pour afficher chacun des tableaux de caractères référencés par words. Utilisez ensuite cette méthode pour afficher les éléments du tableau words à partir de la méthode main.

Écrivez une méthode isPalindrome(char[] word) renvoyant vrai si le mot référencé par word est un palindrome et faux sinon. On vous rappelle qu'un palindrome est un mot qui reste identique si l'on inverse l'ordre des lettres. C'est par exemple le cas du mot « radar ».

Vous pouvez tester la méthode isPalindrome en affichant son résultat lorsque vous l'invoquez avec words[0] (résultat attendu faux) et avec words[1] (résultat attendu vrai).

Pour mettre en œuvre cet algorithme, vous pouvez par exemple parcourir la première moitié du mot (de 0 à word.length/2) avec une variable entière i, et vérifier que pour tout i, word[i] est égal à word[word.length - i - 1].

Quelle est la complexité de la fonction isPalindrome ?

Soit n la taille du tableau en entrée. La complexité est en

\mathcal{O}(n)

Écrivez une méthode printPalindromes(char[][] words) qui n'affiche que les palindromes des tableaux référencés par words.

On cherche maintenant à trouver les anacycliques dans notre tableau de mots. Un anacyclique est un mot qui peut se lire dans les deux sens (aux accents près). Contrairement à un palindrome, lorsqu'on lit un anacyclique de droite à gauche, le mot résultant n'est pas forcément le même que celui obtenu en lisant de gauche à droite. De façon à trouver les anacycliques dans notre liste de mot, on va les réécrire en inversant l'ordre des lettres.

Pour commencer, on vous demande d'écrire une méthode reverseWord(char[] word) qui inverse les lettres dans le tableau word (c'est-à-dire, la lettre à la position i est inversée avec la lettre à la position word.length - i - 1). Vous remarquerez que, comme word est passé par référence, le mot référencé par l'appelant est bien modifié.

Testez votre méthode en inversant le mot words[0] dans la méthode main. Pensez à afficher le mot inverse avec la méthode printWord.

si vous inversez word[i] avec word[word.length - i - 1] puis word[word.length - i - 1] avec word[i], vous allez inverser deux fois les lettres ce qui annule la première inversion !

Quelle est la complexité de la fonction reverseWord ?

Soit n la taille du tableau en entrée. La complexité est en

\mathcal{O}(n)

Pour finir, écrivez une méthode reverseWords(char[][] list) qui inverse l'ordre des lettres de chacun des mots référencés par list. Quels mots et phrases sont des anacycliques ?

Tous les mots, sauf le dernier, sont des anacycliques.

Palindrome.java

Tri à bulles (∼20mn – moyen)

Dans cet exercice, nous étudions un algorithme de tri classique : le tri à bulles. Cet algorithme est toujours inefficace, mais il est intéressant à mettre en œuvre car il est simple. Le tri à bulles est un algorithme de tri en place, c'est-à-dire que l'algorithme trie un tableau désordonné. Le principe de l'algorithme est de faire monter les valeurs les plus hautes en haut du tableau, un peu comme des bulles.

Créez un projet nommé tri et une classe BubbleSort contenant une méthode main. Dans votre méthode main, définissez une variable tab référençant un tableau de doubles et affectez-lui un tableau contenant les valeurs 2.3, 17.0, 3.14, 8.83, 7.26. Affichez chaque élément du tableau.

Il est important que le tableau soit un tableau de double et non de float. En effet, par défaut, Java considère qu'un nombre à virgule flottante est un double et non un float. Le tableau { 2.3, 17.0, 3.14, 8.83, 7.26 } créé par Java est donc un tableau de double, qui ne peut alors pas être affecté à un tableau de float.

Pour faire monter les bulles dans le tableau, nous le parcourons de droite (fin du tableau) à gauche (début du tableau) avec une variable d'indice i. Ensuite, pour chaque i, il faut faire remonter la plus grande valeur jusqu'à l'emplacement i avant de passer à l'itération suivante (i-1). La figure suivante illustre le principe :

État initial    2.3 17.0 3.14 8.83 7.26     i = 4
                                    ^
                                    i

Remonte la plus grande bulle avec j va de 0 à i - 1

=>              2.3 3.14 8.83 7.26 17.0     i = 4
                                    ^
                                    i
c
Recommence avec i = 3

Initialement, i vaut 4 (taille du tableau - 1). Dans cet exercice, n'utilisez pas 4 : les méthodes doivent fonctionner avec n'importe quelle entrée. On parcourt le tableau avec variable j allant de 0 à i - 1 pour faire remonter la plus grande bulle. À chaque fois que tab[j] est plus grand que tab[j+1], il faut donc inverser les deux cases. L'état après ce parcours est donné à la fin de la figure. Ensuite, il suffit de recommencer avec i égal 3 puisque l'élément en tab[4] est bien placé. Vous pouvez observer une mise en œuvre intéressante de cet algorithme ici.

Commencez par écrire une méthode de classe swap prenant en entrée un tableau de double, un indice i et un indice j et modifiant le tableau pour inverser les valeurs stockées en i et j. Cette fonction ne retourne rien (réfléchissez pourquoi).

static void swap(double[] tab, int i, int j) { double temp = tab[i]; tab[i] = tab[j]; tab[j] = temp; }

Écrivez une méthode de classe sort prenant en entrée un tableau de double et qui le trie en place. La méthode ne retourne rien.

static void sort(double[] tab) { int n = tab.length; // On fait remonter les bulles de droite à gauche for (int i = n - 1; i > 0; i--) { for (int j = 0; j tab[j + 1]) { swap(tab, j, j + 1); } } } }

Dans main, triez votre tableau et affichez-le.

// Méthode utilitaire pour afficher un tableau static void printArray(double[] tab) { for (double val : tab) { System.out.print(val + " "); } System.out.println(); } // Méthode main public static void main(String[] args) { double[] tab = { 2.3, 17.0, 3.14, 8.83, 7.26 }; System.out.println("Tableau initial :"); printArray(tab); // Tri du tableau sort(tab); System.out.println("Tableau trié :"); printArray(tab); }

Quelle est la complexité de cet algorithme dans le pire des cas ?

La complexité est quadratique en la taille du tableau dans le pire des cas (deux boucles imbriquées = n + (n-1) + (n-2) + ... + 1).

Tri par insertion (∼30mn – moyen)

Dans cet exercice, nous nous intéressons au tri par insertion. Le principe de cet algorithme est de maintenir un ensemble trié lors de l'insertion d'un nouvel élément. Vous pouvez observer une mise en œuvre intéressante de cet algorithme ici. L'algorithme de tri par insertion est particulièrement efficace pour de petits ensembles à trier, mais totalement inefficace dès que le nombre d'éléments devient grand.

Dans le projet tri, créez une classe InsertionSort contenant une méthode main.

Affichez les arguments de votre programme après avoir spécifié que les arguments sont 4 6 -1 3 5 2.

Créez un tableau tab contenant les arguments du programme, mais représentés par des double.

double[] tab = new double[args.length]; for (int i = 0; i

Créez une méthode classe sort prenant en entrée un tableau de double et retournant un tableau de double. Dans cette méthode, créez un tableau nommé sorted ayant autant de cases que le tableau des arguments du programme. La méthode doit retourner ce tableau.

Complétez votre programme de façon à afficher les éléments du tableau sorted dans la fonction main. Pour cela, appelez la fonction sort sur tab et récupérez la sortie (non triée pour l'instant). Votre programme devrait afficher 6 fois l'entier 0 puisque vous avez 6 arguments et parce qu'un tableau est toujours pré-initialisé avec des 0 en Java.

Pour ajouter les valeurs au tableau sorted tout en maintenant le tableau trié, vous devez itérer sur les arguments. Pour chaque argument, vous devez procéder en trois étapes.

Étape 1: à l'aide d'une boucle, trouvez l'emplacement dest auquel il faut insérer l'argument courant dans le tableau sorted. Pour cela, il suffit de trouver le premier élément qui est plus grand que l'argument à insérer. Notez que vous ne devez comparer que les éléments déjà insérés (c'est-à-dire que vous devez compter le nombre d'éléments insérés dans votre tableau, ça vous évitera de parcourir tout le tableau à chaque fois).
Étape 2: ensuite, décalez d'un cran à droite la partie se trouvant à droite de dest dans le tableau sorted de façon à libérer un espace pour le nouvel entier. Pensez à copier de la droite vers la gauche pour éviter d'écraser vos valeurs.
Étape 3: enfin, insérez le nouvel élément à l'emplacement dest.

Le petit schéma suivant illustre le principe (un point d'interrogation indique qu'aucun élément n'est encore inséré à cet emplacement dans le tableau) :

Insertion de l'élément 8:
  État initial:
    Nombre d'éléments déjà insérés: 0
    Tableau: [? ? ? ? ? ?]
  Étape 1: Trouver la position à laquelle insérer l'élément
    Emplacement d'insertion: 0 (car 8 est plus grand que tous les éléments déjà insérés)
  Étape 2: Décaler d'un cran à droite la partie droite du tableau
    Nombre d'éléments déjà insérés: 0
    Tableau: [? ? ? ? ? ?]
  Étape 3: Insérer l'élément 8
    Nombre d'éléments déjà insérés: 1
    Tableau: [8 ? ? ? ? ?]

...

Insertion de l'élément 3:
  État initial:
    Nombre d'éléments déjà insérés: 3
    Tableau: [1 6 8 ? ? ?]
  Étape 1: Trouver la position à laquelle insérer l'élément
    Emplacement d'insertion: 2 (car l'élément 6 est plus grand que l'élément 3 à insérer)
  Étape 2: Décaler d'un cran à droite la partie droite du tableau
    Nombre d'éléments déjà insérés: 3
    Tableau: [1 6 6 8 ? ?]
  Étape 3: Insérer l'élément 3
    Nombre d'éléments déjà insérés: 4
    Tableau: [1 3 6 8 ? ?]

Commencez par écrire une fonction findInsertion qui prend en entrée un tableau de double (ce sera sorted), l'élément à insérer, et l'indice de fin du tableau et qui retourne un entier représentant la position où insérer notre élément.

static int findInsertion(double[] sorted, double value, int insertedCount) { // On cherche le premier élément strictement plus grand que 'value' for (int i = 0; i value) { return i; } } // Si aucun élément n'est plus grand, on insère en fin de la partie utilisée return insertedCount; }

Écrivez un fonction shift prenant en entrée un tableau de double et un indice. Cette fonction décale en place tous les éléments du tableau d'un cran vers la droite à partir de l'indice donné (et ne retourne rien).

static void shift(double[] sorted, int fromIndex, int insertedCount) { for (int i = insertedCount; i > fromIndex; i--) { sorted[i] = sorted[i - 1]; } // La case 'fromIndex' sera écrasée par l'insertion qui suit }

Finalement, implémentez la fonction sort.

static double[] sort(double[] input) { double[] sorted = new double[input.length]; // pré-initialisé à 0.0 int insertedCount = 0; for (int i = 0; i

Quelle est la complexité du tri par insertion dans le pire des cas ?

Dans le pire des cas, le tableau est trié dans l’ordre décroissant. Chaque nouvel élément doit être inséré tout au début. Donc pour le i-ème élément, il faut décaler i cases. Nombre total de décalages/comparaisons ≈ 1 + 2 + … + (n-1) = n(n-1)/2. On a une complexité de O(n²).

Tri fusion (∼1h10 – moyen – obligatoire)

Le tri étant décidément une réelle passion chez les informaticiens, nous allons étudier un nouvel algorithme de tri appelé l'algorithme de tri fusion (merge sort en anglais). Cet algorithme est intéressant car il peut être mis en œuvre de façon relativement efficace.

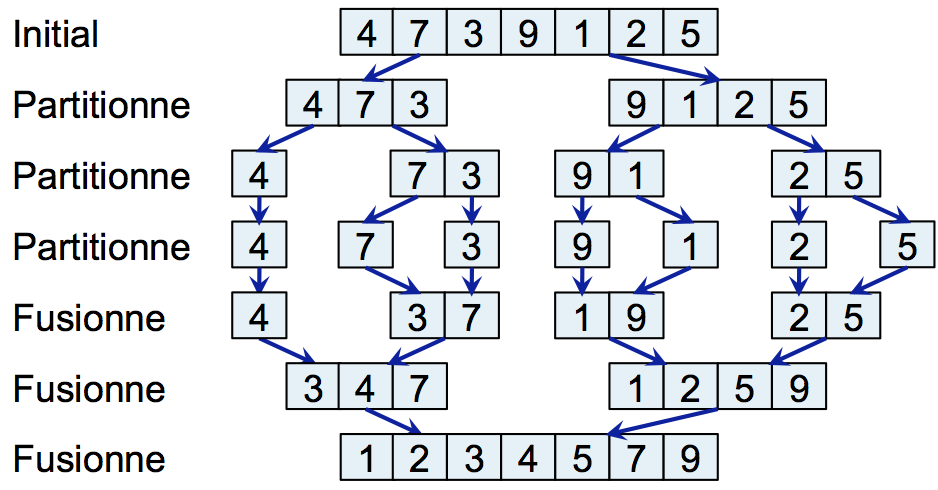
L'algorithme de tri fusion part de l'idée qu'il faut diviser pour mieux régner. Le principe est de prendre un tableau non trié et de le partitionner en deux parties à peu près égales. Ensuite, de façon récursive, l'algorithme trie le tableau de gauche et le tableau de droite. Enfin, l'algorithme fusionne les deux tableaux triés pour construire un tableau contenant tous les éléments triés. Cette opération de fusion est une opération relativement efficace car fusionner des tableaux triés est rapide en terme de temps de calcul.

Le schéma suivant illustre le principe. De façon récursive, l'algorithme commence par partitionner les tableaux jusqu'à obtenir des tableaux de taille 1. Ce tableau de taille 1 est naturellement trié. Ensuite, l'algorithme fusionne les tableaux de façon à reconstruire la liste triée.

Principe du tri fusion.

La mise en œuvre que nous vous proposons dans cet exercice n'est pas optimisée, mais elle a l'avantage d'être relativement simple à comprendre. Cette mise en œuvre est subdivisée en trois parties. Dans la première partie, nous écrivons la méthode qui fusionne des tableaux triés. Dans la second partie, nous écrivons la méthode qui partitionne les tableaux. Enfin, dans la troisième partie nous complétons notre programme en utilisant les deux méthodes précédentes.

Une illustration fantaisiste de l'algorithme est donnée ici.

la fusion

Créez un projet nommé msort contenant une classe MergeSort, elle-même contenant une méthode main. Allouez le tableau d'entiers t1 initialisé avec les valeurs 3, 4, 7 et le tableau d'entiers t2 initialisé avec les valeurs 1, 2, 5, 9.

Écrivez une méthode display prenant en argument un tableau d'entiers et l'affichant dans le terminal. Vérifiez que votre méthode est correcte en l'appelant avec l'argument t1.

Avant de pouvoir fusionner les deux tableaux, nous avons besoin de deux méthodes annexes. La première méthode, nommée int[] right(int[] tab), alloue un tableau de taille tab.length - 1. Elle copie les éléments de droite du tableau tab (c.à-d., à partir de l'élément d'index 1) dans le tableau alloué et renvoie ce nouveau tableau. De façon à tester la méthode right, appelez la dans la méthode main avec l'argument t1, et vérifiez, en affichant le résultat de right avec display, que le nouveau tableau contient 4, 7.

La seconde méthode annexe se nomme int[] merge(int val, int[] tab) et effectue l'opération inverse : elle renvoie un nouveau tableau dont le premier élément est val suivi d'une copie des éléments de tab. Vérifiez que votre méthode est correcte en affichant le résultat de merge(1, t1).

Nous pouvons maintenant mettre en œuvre la fusion. Pour cela, vous allez écrire une nouvelle méthode nommée merge, prenant en argument deux tableaux t1 et t2 triés et renvoyant la fusion de ces deux tableaux. Le fait qu'il y ait deux méthodes merge ne pose pas de problème, car les arguments des deux méthodes sont différents, ce qui permet à Java de savoir quelle méthode on souhaite appeler en fonction des paramètres.

Nous mettons en œuvre merge de façon récursive :

Si t1 a une taille égale à zéro, alors merge doit renvoyer t2
Si t2 a une taille égale à zéro, alors merge doit renvoyer t1
Si t1[0] est plus petit que ou égal à t2[0], alors merge doit renvoyer le tableau construit à partir de t1[0] et du résultat de la fusion de la partie droite de t1 avec le tableau t2. La partie droite de t1 s'obtient en appelant la méthode right et l'ajout à gauche de t1[0] s'obtient en appelant la seconde méthode merge que vous avez défini à la question précédente.
Dans le cas inverse, il suffit d'appeler merge en inversant les rôles de t1 et t2.

Testez merge en affichant le résultat de la fusion de t1 et t2 dans la méthode main.

MergeSort.java

Quelle est la complexité de la fonction merge prenant en entrée deux tableaux ?

Tout d'abord, on note que les fonctions right et int[] merge(int val, int[] tab) sont linéaires en la taille du tableau en entrée, car elles demandent de recopier le tableau donné en entrée. Ensuite, nous allons exprimer la complexité de merge en fonction de la somme des tailles des deux tableaux en entrée que nous appelons n.
Les deux cas les plus couteux sont les deux derniers. On note que le dernier cas se produit au maximum n fois. L'avant-dernier cas nous donne la relation de récurrence suivante:

C(n) = n + C(n-1)

Où le n vient de right et int[] merge(int val, int[] tab). On appelle ensuite merge avec un élément en moins dans un des tableaux. À partir de là, nous avons:

C(n) = \sum_{i=1}^n i = \frac{n(n+1)}{2} = \mathcal{O}(n^2)

La complexité finale de merge est donc quadratique.

(Optionnel) Cette complexité vous semble-t-elle optimale ? Pourriez-vous proposer un autre algorithme ? Quelle est sa complexité ?

Le problème de l'algorithme présenté plus haut est qu'il recopie beaucoup de fois des tableaux. Au lieu d'avoir un algorithme récursif, nous pourrions avoir un algorithme itératif fonctionnant de la manière suivante :

Création du tableau final de taille égale à la somme des deux tailles.
Pour chacune des deux tableaux t0 et t1, nous conservons indice i0 et i1 nous indiquant notre position dans chaque tableau. Ces indices sont initialisés à 0 et seront incrémenté de 1 à chaque fois qu'un élément sera ajouté au tableau final.
Tant que les deux indices ne sont pas égaux à la taille de leur tableau respectif, prendre la valeur la plus petite entre t0[i0] et t1[i1] et la rajouter au tableau final. Incrémenter la valeur de l'indice ayant amené l'ajout.

On peut écrire un algorithme de complexité linéaire en ayant pour chaque tableau un pointeur sur la position actuelle que l'on avance au moment opportun.

MergeSort2.java

le partitionnement

Dans cette partie, nous nous occupons de partitionner un tableau.

Commencez par supprimer les tests actuels de la méthode main (les définitions des t1 et t2 incluses). À la place, allouez un tableau d'entiers nommé tab initialisé à 4, 7, 3, 9, 1, 2, 5.

Écrivez une méthode int[] extract(int[] tab, int start, int end) qui extrait de tab le sous-tableau commençant à l'indice start inclus et finissant à l'indice end non inclus. Testez votre méthode extract en affichant le résultat de l'extraction de la moitié gauche de tab dans la méthode main. Vous devriez obtenir le tableau 4, 7, 3.

le tri fusion

Nous pouvons enfin mettre en œuvre l'algorithme du tri-fusion.

Écrivez une méthode int[] mergeSort(int[] tab) mettant en œuvre l'algorithme de tri fusion pour renvoyer un tableau contenant les éléments de tab triés.

Pour vous guider, nous vous proposons d'utiliser un algorithme récursif :

Si tab a une taille inférieure ou égale à 1, alors le tableau est déjà trié et il suffit de le renvoyer.
Sinon, il faut appeler mergeSort sur la partie gauche de tab, puis mergeSort sur la partie droite de tab et enfin utiliser merge pour fusionner les résultats des deux appels à mergeSort.

MergeSort.java

MergeSort2.java

Quelle est la complexité de mergeSort ?
On rappelle que :

\sum_{n = 1}^{\infty} (\frac{1}{n^{2}}) \leq 2

Nous partons du principe que la complexité de merge est quadratique (c.f. plus haut). Dans ce cas, à chaque appel à mergeSort, nous exécutons au pire deux nouveaux mergeSort avec des tableaux deux fois plus petits et une fusion. La complexité de extract étant linéaire, on peut l'ignorer au profit de merge qui est quadratique. On a donc la relation de récurrence :

C (n) = n^{2} + 2 C (\frac{n}{2}) = n^{2} + 2 * (\frac{n}{2})^{2} + 4 C (\frac{n}{4}) = n^{2} (1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + . . .) \leq 2 * n^{2}

La complexité est donc quadratique.
En réalité, la complexité avec un merge efficace est

\mathcal{O}(nlog(n))

, ce qui est la complexité optimale pour un algorithme de tri ! En effet, la relation de récurrence devient :

C (n) = n + 2 C (\frac{n}{2}) = n + 2 * \frac{n}{2} + 4 C (\frac{n}{4}) = n * (1 + 1 + 1 + 1 + . . .) = O (n * l o g (n))

Le log vient du fait que l'on divise n par deux jusqu'à obtenir un nombre inférieur à 1.

Félicitations ! Vous venez de mettre œuvre votre premier algorithme complexe en Java !

Tri rapide (∼1h15 – moyen – entraînement)

L'algorithme de tri rapide (quick sort en anglais) est un des algorithmes de tri les plus efficaces connus : c'est un algorithme qui a une complexité moyenne optimale, même si cet algorithme peut devenir inefficace dans des cas pathologiques. De plus, l'algorithme de tri rapide est un algorithme de tri en place, c'est-à-dire qu'il ne nécessite pas de tableau annexe pour trier les éléments. L'algorithme de tri fusion que vous avez étudié dans l'exercice précédent a aussi une complexité moyenne optimale, mais il nécessite un tableau annexe, ce qui rend le tri rapide plus efficace en pratique.

L'algorithme de tri rapide part aussi de l'idée qu'il faut diviser pour mieux régner. Toutefois, contrairement au tri rapide, lorsque l'algorithme de tri rapide divise le tableau en deux parties, le tri rapide s'assure que tous les éléments du tableau de gauche sont plus petits que tous les éléments du tableau de droite. Finalement, il n'y a donc pas besoin de fusionner les tableaux comme dans le tri fusion puisque les tableaux de gauche et de droite sont déjà bien placés.

Pour y arriver, le tri rapide choisit un élément appelé pivot dans le tableau. Le choix de ce pivot est libre, mais on prend en général l'élément le plus à droite du tableau. Ensuite, l'algorithme place ce pivot à sa place définitive en s'assurant que tous les éléments à gauche du pivot sont plus petits que le pivot et que tous les éléments à droite du pivot sont plus grands. On peut remarquer que, comme le pivot est choisi de façon arbitraire, le tableau de gauche et le tableau de droite ont une taille quelconque. À l'étape suivante, on trie de manière récursive les tableaux de gauche et de droite.

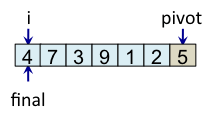
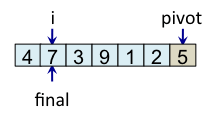
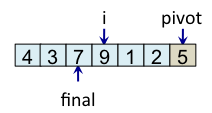
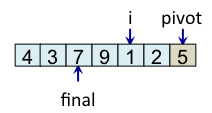
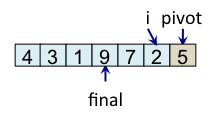
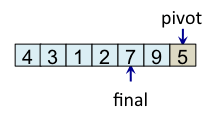
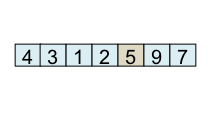
Le schéma ci-dessous illustre l'étape de partitionnement. Après avoir choisi l'élément de droite comme pivot, c'est-à-dire l'élément 5, l'algorithme initialise i et final à 0. L'indice i sert à parcourir le tableau alors que l'indice final sert à savoir quelle sera la place finale du pivot.

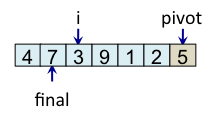
Le principe de l'algorithme est de n'incrémenter final qu'après s'être assuré que l'élément à la place final (et donc tous les éléments à gauche de final) est strictement plus petit que le pivot. Par exemple, lorsque i est égal à 1, l'élément à l'indice final (7) est plus grand que le pivot (5), donc l'algorithme n'incrémente pas final. En revanche, dès que l'algorithme s'aperçoit qu'un élément pourrait être bien placé en échangeant des éléments, l'algorithme incrémente final. C'est, par exemple, le cas lorsque i est égal à 2. Dans ce cas, l'élément à la place final vaut 7, l'élément à la place i vaut 3 et l'élément pivot vaut 5. Comme 3 est plus petit que 5, il suffit d'inverser 3 et 7 pour que l'élément à la place final devienne strictement plus petit que le pivot. Une fois cette inversion effectuée, on peut incrémenter final puisque 3 est maintenant bien placé. À la fin de l'étape de partitionnement, on est assuré que les éléments à gauche de final sont strictement plus petits que le pivot, alors que les éléments à droite de final sont plus grands ou égaux. Il suffit alors de déplacer le pivot à la place final, comme illustré à l'étape fin, puis de trier les tableaux de gauche et de droite.

i=0		Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final
i=1		Teste si tab[i] < pivot faux => ne fait rien
i=2		Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final
i=3		Teste si tab[i] < pivot faux => ne fait rien
i=4		Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final
i=5		Teste si tab[i] < pivot vrai => échange tab[i] et tab[final] et incrémente final
i=6		i atteint pivot => échange pivot avec tab[final]
Fin		État à la fin du partitionnement Ce qui est à gauche du pivot est plus petit que ce qui est à droite

Une illustration folklorique de l'algorithme est donnée ici.

Créez un projet nommé qsort contenant une classe QuickSort, elle-même contenant une méthode main. Allouez le tableau d'entiers tab initialisé avec les valeurs 4, 7, 3, 9, 1, 2, 5, écrivez une méthode display pour afficher le tableau et testez-la avec tab.

Avant de s'occuper du partitionnement, nous commençons par une méthode annexe appelée swap. Cette méthode prend en argument un tableau d'entiers et deux indices et inverse les éléments se trouvant à ces indices. Testez votre méthode en inversant les éléments aux positions 0 et 4 de tab et en affichant le tableau.

Écrivez une méthode partition prenant en argument un tableau d'entiers et deux indices nommés start et end, et renvoyant un entier. Cette méthode doit appliquer l'algorithme de partitionnement décrit au début de l'exercice sur le sous-tableau se trouvant entre start et end inclus. La méthode doit renvoyer l'emplacement final (remarque : final étant un mot clé du langage Java, nommez votre variable f). Testez votre méthode en appelant partition(tab, 0, tab.length - 1) dans la méthode main, et vérifiez que le tableau est bien celui indiqué à la dernière étape de l'illustration.

Quelle est la complexité de la méthode partition ?

On parcourt tout le tableau. La complexité est donc linéaire en la taille du tableau.

Écrivez une méthode quicksort prenant en argument un tableau d'entiers et deux indices nommés start et end. Cette méthode doit trier récursivement le tableau se trouvant entre start et end inclus.

Si la différence entre end et start est inférieur ou égale à zéro, le tableau à une taille inférieure ou égale à 1, ce qui signifie que le sous-tableau est trié. Il ne faut donc rien faire.
Sinon, c'est que le tableau a une taille au moins égale à deux. La méthode doit donc :
- Appeler partition pour partitionner le tableau et stocker l'indice final dans une variable locale,
- Appeler quicksort avec la partie gauche du tableau (entre start et final - 1) et quicksort avec la partie droite du tableau (entre final + 1 et end).

Testez votre méthode quicksort en appelant quicksort(tab, 0, tab.length - 1) dans votre méthode main. Vérifiez que le tableau est bien trié en appelant display.

Finalement, écrivez une seconde méthode quicksort ne prenant qu'un tableau d'entiers en argument, et appelant la seconde méthode quicksort de façon à trier entièrement le tableau passé en argument.

QuickSort.java

Quelle est la complexité de la méthode quicksort dans le pire des cas ? Mettez en évidence ce que sont les pires cas et les meilleurs cas et donnez leurs complexités.

Dans le cas général, on a l'équation de récurrence qui dépend de la position du pivot j à la fin de la fonction partition. Le meilleur des cas se produit quand nous découpons à chaque partitionnement le tableau en deux. Intuitivement, on divise la complexité du problème par deux à chaque appel. Ce schéma est assez récurrent, par exemple avec le tri fusion vu plus haut.
En créant l'équation de récurrence dans ce cas, on retrouve la même que pour le tri fusion vu plus haut (en sachant que la méthode partition est linéaire). On retrouve donc une complexité de

\mathcal{O}(nlog(n))

.
Le pire des cas se produit quand le tableau est déjà trié. Dans ce cas, la fonction partition ne fait rien, mais a quand même un coup linéaire. L'équation de récurrence devient :

C(n) = n + C(n-1) = \sum_{i=1}^n i = \mathcal{O}(n^2)

La complexité est donc quadratique en la taille du tableau.

En réalité, la complexité moyenne du tri rapide est en

\mathcal{O}(nlog(n))

. Comme il a l'avantage d'avoir une complexité en mémoire faible, c'est cet algorithme qui est utilisé dans la majorité des cas.

Dans cette partie, nous avons considéré que le pivot était le dernier élément du tableau. En considérant la réponse à la question précédente, comment peut-on choisir la valeur pivot pour toujours avoir une complexité en

\mathcal{O}(nlog(n))

? Pourquoi cette solution n'est-elle pas utile en pratique ?

Si l'on choisit la médiane comme point de pivot, on se trouvera toujours dans le meilleur des cas. Ce cas correspond à une division en deux parts égales du tableau initial.
Cependant, cette solution n'est pas adaptée, car trouver la médiane n'est pas gratuit ! Un algorithme trivial trouve la médiane en temps quadratique (un algorithme optimal trouve la médiane en temps linéaire, mais c'est très compliqué).

Félicitations ! Vous savez maintenant trier des tableaux en Java !

Comparaison des performances (entraînement)

Rédigez une méthode de classe evaluatePerformance en Java qui mesure les performances de vos tris (on la copiera et adaptera dans chaque classe). La méthode prend deux paramètres : nElements (taille des tableaux) et nExperiments (nombre d’expériences). Pour chaque expérience, elle génère un tableau aléatoire de taille nElements, le trie avec votre algorithme, mesure le temps écoulé, additionne ce temps, puis affiche le temps moyen (temps total divisé par nExperiments).

Pour générer des nombres aléatoires en Java, vous pouvez utiliser java.util.Random : Random rand = new Random(); double x = rand.nextDouble(); (valeur dans [0.0, 1.0)). Il vous faudra ajouter en haut de votre fichier import java.util.Random; (on verra pourquoi plus tard).

Pour chronométrer, utilisez l’horloge haute résolution System.nanoTime(). Exemple : long t0 = System.nanoTime(); exécutez le tri, puis long t1 = System.nanoTime();. Le temps écoulé en millisecondes vaut double elapsedMs = (t1 - t0);.

Comparez les performances des algorithmes. Est-ce que cela correspond bien aux complexités observées ?

static double testPerformance(int nElements, int nExperiments) { Random rand = new Random(); long totalTime = 0; for (int exp = 0; exp

Histogramme (∼30mn – moyen – entraînement)

Écrivez un programme permettant de représenter un histogramme sur un écran (voir figure ci-dessous) à partir d'un tableau tab d'entiers.

      *   
    * *   
  * * **  
  * * **  
+++++*++++
** *    **
 * *    * 
 *

L'histogramme doit être cadré en haut à gauche de l'écran. Chaque colonne i contient un nombre d'étoiles égal à la valeur de tab[i]. L'axe des abscisses est représenté comme une ligne de '+', mais si tab[i] vaut 0, votre programme doit afficher un '*'. L'histogramme représenté sur la figure correspond au tableau suivant :

int[] tab = { -1, -3, 2, -2, 3, 0, 4, 2, -2, -1 };

On fait l'hypothèse que le tableau est compatible avec la taille de l'écran.

Pour réussir l'exercice, il faut savoir que System.out.print(char c) affiche le caractère c sans ajouter retour à la ligne, alors que System.out.println() affiche juste un retour à la ligne.

Commencez par écrire une boucle qui trouve les valeurs minimum et maximum du tableau.

De façon à imposer que la ligne 0 soit affichée même lorsque le minimum et le maximum sont strictement supérieurs (resp. strictement inférieurs) à 0, vous devez pré-initialiser ces minimums et maximums à 0 avant de parcourir le tableau.

À l'aide d'un indice line parcourez l'ensemble des valeurs se trouvant entre le maximum et le minimum dans le sens décroissant. À chaque tour de boucle, vous devez parcourir, avec l'indice col, le tableau et afficher le caractère adéquat.

Vous devez afficher une étoile dans trois cas :
- si line est égal à 0 et si tab[col] est égal à 0,
- si line est strictement supérieur à 0, si tab[col] est strictement supérieur à 0 et si tab[col] est plus grand que line,
- si line est strictement inférieur à 0, si tab[col] est strictement inférieur à 0 et si tab[col] est plus petit que line.
Si vous n'affichez pas une étoile, vous devez afficher un caractère blanc lorsque line est différent de 0, et le caractère + lorsque line est égal à 0.

Histogram.java

Quelle est la complexité de l'algorithme en fonction du tableau utilisé ? Réfléchissez à quelles sont les propriétés du tableau qui doivent entrer en jeu.

Nous allons avoir besoin de la taille n du tableau, ainsi que de la valeur maximale M et la valeur minimale N.
Trouver le maximum et le minimum est linéaire en la taille du tableau. Pour afficher l'histogramme, nous devons faire une boucle entre le min et le max. Dans cette boucle, nous avons une autre boucle sur la taille du tableau. La complexité finale est donc

\mathcal{O}((M - m) * n)

Sudoku (∼1h30 – ninja – entraînement)

Le but de cet exercice est de concevoir un algorithme permettant de résoudre un sudoku. Un sudoku est défini par une grille de 9 colonnes sur 9 lignes. Chaque case doit contenir un nombre compris entre 1 et 9 inclus. Le but du jeu est de remplir la grille de façon à ce que chacun des chiffres compris entre 1 et 9 apparaisse au plus une fois dans (i) chaque ligne, (ii) chaque colonne et (iii) chacun des sous-carrés représentés sur la figure ci-dessous. Au début du jeu, une vingtaine de chiffres sont déjà placés dans la grille et le joueur doit trouver les chiffres se trouvant dans les autres cases.

 ----------------------------------
 |  .  1  . |  6  .  7 |  .  .  4 |
 |  .  4  2 |  .  .  . |  .  .  . |
 |  8  7  . |  3  .  . |  6  .  . |
 ----------------------------------
 |  .  8  . |  .  7  . |  .  2  . |
 |  .  .  . |  8  9  3 |  .  .  . |
 |  .  3  . |  .  6  . |  .  1  . |
 ----------------------------------
 |  .  .  8 |  .  .  6 |  .  4  5 |
 |  .  .  . |  .  .  . |  1  7  . |
 |  4  .  . |  9  .  8 |  .  6  . |
 ----------------------------------

La grille résolvant le sudoku représenté ci-dessus se trouve ci-dessous :

 ----------------------------------
 |  9  1  3 |  6  2  7 |  5  8  4 |
 |  6  4  2 |  5  8  9 |  7  3  1 |
 |  8  7  5 |  3  4  1 |  6  9  2 |
 ----------------------------------
 |  5  8  9 |  1  7  4 |  3  2  6 |
 |  2  6  1 |  8  9  3 |  4  5  7 |
 |  7  3  4 |  2  6  5 |  8  1  9 |
 ----------------------------------
 |  1  2  8 |  7  3  6 |  9  4  5 |
 |  3  9  6 |  4  5  2 |  1  7  8 |
 |  4  5  7 |  9  1  8 |  2  6  3 |
 ----------------------------------

Pour commencer, créez un projet nommé sudoku avec une classe Sudoku contenant une méthode main.

Une grille de sudoku est représentée par un tableau de 81 cases (9 lignes sur 9 colonnes). Si une case vaut 0, c'est qu'elle n'est pas encore initialisée, sinon, c'est qu'elle contient une valeur. Pour commencer, copiez-collez le code ci-dessous permettant de créer une grille. Ensuite, ajoutez une boucle permettant d'afficher la grille. Vous veillerez à afficher un point si la case contient 0. Vous devriez obtenir un affichage proche de celui utilisé pour la grille d'exemple, mais sans la représentation des carrés internes.

int grid[] = {
  0, 1, 0, 6, 0, 7, 0, 0, 4, 
  0, 4, 2, 0, 0, 0, 0, 0, 0, 
  8, 7, 0, 3, 0, 0, 6, 0, 0, 
  0, 8, 0, 0, 7, 0, 0, 2, 0, 
  0, 0, 0, 8, 9, 3, 0, 0, 0, 
  0, 3, 0, 0, 6, 0, 0, 1, 0, 
  0, 0, 8, 0, 0, 6, 0, 4, 5, 
  0, 0, 0, 0, 0, 0, 1, 7, 0,
  4, 0, 0, 9, 0, 8, 0, 6, 0 
};

Nous vous proposons de résoudre votre grille avec une méthode de retour arrière (backtracking en anglais). Cette méthode consiste à tenter des valeurs et, si elles ne permettent pas de résoudre la grille, de revenir en arrière pour essayer une nouvelle valeur. Comme nous aurons besoin de modifier la grille pour tenter des valeurs, il faut savoir quelles valeurs sont données initialement et quelles valeurs sont tentées. Vous devez donc définir un tableau de booléens nommé fixed et assigner à vrai la valeur d'une case si et seulement si la case contient initialement une valeur (c'est-à-dire si la case correspondante dans grid a une valeur différente de 0 initialement).

Modifiez votre programme de façon à ce qu'il résolve le sudoku. Comme expliqué auparavant, le principe de l'algorithme est de parcourir la grille du début à la fin en tentant des valeurs. Dès qu'il est impossible de résoudre la grille avec une valeur précédemment rentrée, il faut revenir en arrière.

À haut niveau, il faut parcourir la grille avec une variable cur. Cette variable est initialisée à 0 et l'algorithme boucle tant que cur n'a pas atteint 81 (ce qui signifie que la grille a été résolue) et que cur n'est pas passé en dessous de 0 (ce qui signifie que la grille ne peut pas être résolue).

Pour un cur donné, l'algorithme doit tenter une nouvelle valeur sur la case grid[cur] (si cette dernière n'est pas donnée initialement) en incrémentant sa valeur. Si cette valeur atteint 10, c'est qu'une valeur tentée dans une case précédente ne permet pas de résoudre la grille. Il faut donc revenir en arrière. Sinon, si cette nouvelle valeur entre en conflit avec une valeur se trouvant dans la grille, il faut essayer la valeur suivante. Enfin, si la nouvelle valeur ne rentre pas en conflit, l'algorithme peut essayer de résoudre le reste de la grille en passant à la case suivante.

Techniquement, à chaque pas de boucle :

Si la case cur est initialement donnée, il faut avancer cur de 1,
Sinon, il faut incrémenter la case grid[cur]. Ensuite :
- Si cette case vaut 10, c'est qu'une des valeurs tentées dans une case précédente ne permet pas de résoudre la grille. Il faut donc :
  - Remettre le contenu de la case 0,
  - Remonter cur jusqu'à la première précédente case qui n'est pas donnée initialement (pensez à utiliser fixed pour savoir si une case est donnée ou non initialement).
- Sinon, l'algorithme doit vérifier que la nouvelle valeur de grid[cur] est valide, c'est-à-dire qu'elle ne duplique pas une valeur dans une colonne, une ligne ou un des 9 carrés. Si la valeur est valide, l'algorithme peut avancer cur de 1 pour tenter une valeur sur la case suivante. Si la valeur est invalide, il ne faut rien faire : lors du tour de boucle suivante, la valeur suivante de grid[cur] sera tentée.

Vérifier qu'une valeur est valide n'est pas évident. Nous vous conseillons d'effectuer une unique boucle avec une variable i allant de 0 à 9. Dans cette boucle, il faut vérifier que :

la valeur se trouvant sur la colonne de cur en i^ième ligne est différente de grid[cur],
la valeur se trouvant sur la ligne de cur en i^ième colonne est différente de grid[cur],
la i^ième case du carré interne est différente de grid[cur],

Nous vous conseillons d'utiliser 7 variables pour vérifier que la grille la dernière valeur tentée est valide :

line : indique sur quelle ligne se trouve cur : cur / 9,
col : indique sur quelle colonne se trouve cur : cur % 9,
sline : indique la première ligne du carré interne dans lequel se trouve cur : (line / 3) * 3,
scol : indique la première colonne du carré interne dans lequel se trouve cur : (col / 3) % 3,
icol : indice de la case à la i^ième ligne de la colonne de cur : line * 9 + i,
iline : indice de la case à la i^ième colonne de la ligne de cur : i * 9 + col,
isquare : indice de la i^ième case du carré interne de cur : 9 * (sline + (i / 3)) + scol + (i % 3).

Sudoku.java

Mise en pratique des tris (entraînement)

Les algorithmes de tri sont très utiles dans de nombreuses situations pour résoudre de nombreux problèmes. Dans les exercices qui suivent, il vous faudra utiliser de manière intelligente des tris. Pour cela, vous pouvez soit utiliser les algorithmes implémentés au-dessus (MergeSort et QuickSort), soit directement utiliser la méthode de classe fournie par Java. Avec cette option, il vous faut ajouter en haut de votre fichier la ligne (voir CI4) :

import java.util.Arrays;

Ensuite, vous pourrez utiliser la méthode Arrays.sort qui va trier sur place (pas besoin d'affecter une nouvelle variable, la fonction modifie le tableau donné en entrée). Par exemple :

int[] tableau = {2, 5, 17, 3, 6, 1};
Arrays.sort(tableau);
    

Dans cette section, vous êtes libres de créer de nouveaux fichiers pour chaque question. N'oubliez pas de tester votre code en suivant une procédure similaire aux exercices précédents.

Nous supposons que nous avons un tableau contenant un élément majoritaire, c'est-à-dire un élément apparaissant dans plus de la moitié des éléments du tableau. Trouvez cet élément.

Exemple 1. Entrée : {4, 2, 4}, Sortie : 4
Exemple 2. Entrée : {8, 8, 2, 8, 2, 2, 1, 8, 8}, Sortie : 8

MajorityFinder.java

Écrivez une méthode prenant en entrée un tableau et retournant vrai si le tableau contient au moins un élément en double et faux sinon.

Exemple 1. Entrée : {2, 5, 3, 19, 42}, Sortie : false
Exemple 2. Entrée : {1, 4, 3, 4, 19}, Sortie : true

Duplicate.java

Soient deux chaînes de caractères s et t représentées par des char[]. (Si vous voulez utiliser des Strings, vous pouvez obtenir un char[] depuis un String en faisant s.toCharArray(), voir CI4). Écrivez une fonction qui retourne si s est une anagramme de t , i.e., si en changeant l'ordre de lettres dans s, on peut obtenir t.

Anagram.java

Quand les scientifiques écrivent des articles, ils peuvent faire référence à d'autres travaux et articles. C'est ce qu'on appelle une citation. Le nombre de citations qui fait référence à un article montre l'impact qu'il a eu sur la communauté. Pour savoir l'impact d'un ou une scientifique, on agrège le nombre de citations de tous ses articles dans une seule métrique : le h-index. Le h-index est le plus grand nombre h tel que le scientifique possède h articles avec plus de h citations.
Étant donné un tableau d'entiers représentant les citations d'un ou une scientifique, écrire une fonction calculant son h-index.

Exemple 1. Entrée : {2, 0, 13, 24}, Sortie : 2
Exemple 2. Entrée : {12, 6, 7, 13}, Sortie : 4
Exemple 3. Entrée : {1, 38, 12, 3}, Sortie : 3

HIndex.java