Exercices en vrac JFlex et CUP
Comment perdre une fusée ? (JFlex/CUP impossible !)
L’excès de sucre syntaxique nuit gravement à la santé des compilateurs ! (JFlex/CUP impossible !)
Conflit lexical/Syntaxique
Expliquez le conflit produit par l'introduction des classes génériques dans Java 1.5. Pourquoi cela viole le principe de séparation entre le niveau lexical et le niveau syntaxique ?
Solution dans javac OpenJdk
Solution dans le compilateur JDT d'eclipse
Expliquer la solution par réécriture de la grammaire dans le compilateur incrémental d'eclipse : Generic-JDT-src.txt.
Une Solution simple, mais incorrecte
Une solution dans une grammaire java fournie avec l'outil (LL) AntLR :
Java Cold Case
Bien que présent depuis Java 5 (2004), le problème d'analyse lexical contextuelle des types génériques n'est signalé dans la spécification officielle du langage que depuis Java 17 (2021)(section 3.5) : Generic-JAVA-Lex-Spec.txt.
Postscriptum de l'auteur
Pour écrire l'énoncé de cet exercice, il a fallu remplacer à la main de l'ordre de 60 < ou > par des < ou >. Merci Html !
AEIOUY (JFlex seul)
On reconnaitra en même temps, les mots qui contiennent exactement 6 voyelles dans le bon ordre, et les mots qui contiennent plus de voyelles dont 6 sont dans le bon ordre.
Nombres "aérés" (JFlex seul)
Un usage courant dans le monde anglo-saxon est d'aérer l'écriture des grands nombres avec des séparateurs pour les milliers et les puissances de milliers. Écrire une expression régulière qui reconnaît exactement les nombres entiers avec des séparateurs "tiret bas" autorisés uniquement pour les milliers et les puissances de milliers. On testera avec un analyseur JFlex ligne à ligne qui accepte les nombres aérés valides sur une ligne complète.
Un fichier d'exemples :
Caractères non imprimables, filtre cat -A (JFlex seul)
Pour cet exercice, remplacer l'utilisation du fichier Jflex.include par la version adaptée Jflex8bits.include.
Constantes entières Java (JFlex seul)
- Les "Constantes Entières" représentent des valeurs fixes pour les types primitifs : byte, short, int, et long.
- Les "Constantes Entières" peuvent s'écrire en utilisant les systèmes de numération : décimal, hexadécimal, octal, et binaire.
- Une "Constante Décimale" utilise les chiffres 0 à 9.
- Une "Constante Hexadécimal" utilise les chiffres 0 à 9 et les lettres a à f et A à F. La notation commence alors par le préfixe 0x ou 0X.
- Une "Constante Octal" utilise les chiffres 0 à 7. La notation commence alors par le préfixe 0.
- Une "Constante Binaire" utilise les chiffres 0 et 1. La notation commence alors par le préfixe 0b ou 0B.
- Une "Constante Entière" est analysée par défaut comme un int (valeur sur 4 octets).
- Une "Constante Entière" peut aussi être analysée comme un long (valeur sur 8 octets). Pour cela, on ajoute le suffixe l ou L à la représentation de la constante.
- Pour la lisibilité, on peut insérer, éventuellement de façon consécutive, des caractères tiret bas dans la représentation d'une "Constante Entière".
- En VO dans la spécification :
You can place underscores only between digits; you cannot place underscores in the following places:
- At the beginning or end of a number.
- Adjacent to a decimal point in a floating point literal.
- Prior to an F or L suffix.
- In positions where a string of digits is expected.
- Le 0 qui sert de préfixe à la notation octale est aussi considéré comme le premier chiffre de cette notation. Il peut donc être directement suivi par des caractères _.
- La seule constante décimale commençant par 0 est le nombre 0 (sinon conflit avec l'octal).
- + et - n'apparaissent pas dans la notation des "Constante Entières" mais sont gérés par Java comme des opérateurs au niveau syntaxique. Ainsi, une "Constante Décimal" n'est jamais négative.
- Typo. : les 0 dans l'énoncé sont toujours des chiffres zéro et pas des lettres O.
- Reconnaît séparément chacune des sous-catégories : Décimal, Octal, Hexadécimal et Binaire.
- Reconnaît les commentaires de style C++ (//... fin_ligne) et ainsi ignore les constantes entières à l'intérieur des commentaires.
- Reconnaît les identificateurs et ainsi ignore les constantes entières à l'intérieur d'un identificateur.
- Reporte l'ensemble du source en sortie avec un marquage claire des constantes entières reconnues.
Mot de Passe (JFlex seul)
- contient au moins six caractères,
- contient au moins une minuscule, une majuscule, un chiffre et une ponctuation (Catégorie Unicode \p{Punctuation}),
- ne contient pas comme sous-mot : mot, pass, 666, qwer, azer,
- contient au moins un chiffre hors d'une séquence de chiffres en fin de mot,
- contient au moins un chiffre hors d'une séquence de chiffres en début de mot.
- contient plus de 15 caractères,
- contient des caractères de fin de ligne,
- contient des caractères blancs,
- contient des caractères 8 bits (non 7 bits),
- contient des caractères de contrôle. ([\x00-\x1F\x7F]).
Nombres Romains (JFlex seul)
| I | V | X | L | C | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
On a donc les premiers nombres :
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
On fournit le code Java romGen.java qui génère les nombres romains de 1 à N.
Nombre romain valide
Écrire un analyseur lexical qui reconnaît ligne à ligne les nombres romains entre 1 et 4999. Tester avec les nombres valides (romGen) et un fichier de contre-exemples bien choisis.
Fonction Calculus
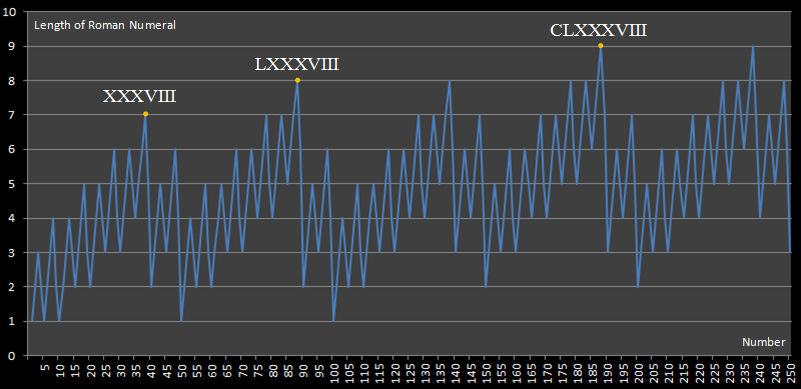
On appellera Calculus d'un nombre, le nombre de chiffres utilisés dans son écriture romaine. Calculus(CXXIV)=5.
Modifier l'analyseur pour :
- écrire la valeur maximum du Calculus des nombres du fichier,
- écrire les Maxima Locaux de Calculus, c'est à dire la première entrée qui a un Calculus de 1, puis de 2,..,
- écrire la fréquence de chaque valeur de Calculus, c'est à dire combien d'entrées ont pour Calculus 1, 2,...
Un exemple de résultat :
Déclinaison latine de calculus : calculus, calcule, calculum, calculi, calculo, calculo
et au pluriel calculi, calculi, calculos, calculorum, calculis, calculis.
Commentaire HTML (JFlex seul)

Sous une forme plus claire, un commentaire HTML 5.0 :
- commence par la séquence <!--,
- se poursuit avec un text avec les contraintes :
- text peut être vide,
- text ne commence pas par >,
- text ne commence pas par ->,
- text ne contient pas --,
- text ne termine pas par -.
- termine par la séquence -->,
- On ajoutera que text peut contenir n'importe quelle séquence de caractères ASCII, y compris les fin de ligne (\n, \r, \r\n).
Exemples de commentaires valides ou non valides :
Analyse lexicale
Écrire une expression régulière qui reconnaît strictement les commentaires conformes à la spécification HTML 5.
Écrire une spécification JFlex pour valider cette expression régulière. Pour chaque commentaire valide, on imprimera le commentaire clairement délimité.
Entête de Mail RFC822 (JFlex seul)
La syntaxe d'un courriel est décrite dans le RFC 822 (Syntaxe BNF complète en annexe D, version simplifiée en annexe B).
Elle peut être synthétisée comme suit :
- Un message complet est la concaténation d'un nombre quelconque de champs-entête, d'une ligne vide
(\n\n), et d'un corps de message.
Contrairement au RFC, on pourra supposer qu'il y a toujours au moins 1 champs-entêtes et que le corps est non vide. - Un champs-entête est la concaténation d'un nom-champs, du caractère :, est d'un corps-champs.
- Un champs-entête commence sur un début de ligne et termine sur une fin de ligne, mais peut occuper plusieurs lignes. Pour éviter les ambiguïtés, les lignes de continuation dans un corps-champs doivent obligatoirement commencer par un caractère espace ou tabulation.
- Le corps d'un message et les corps-champs sont constituées de caractères ASCII 7-bits quelconques.
- Les nom-champs contiennent au moins un caractère et sont constituées des caractères imprimables (ASCII de 33 à 126) à l'exception du caractère espace et du caractère :.
Analyse lexicale sans super-état
Écrire un analyseur lexical sans utiliser les super-états qui lit un mail, vérifie la syntaxe et identifie les unités lexicales champs-entête et corps de message.
Pour chaque unité lexicale, on imprimera le contenu multi-ligne de l'unité de manière clairement délimitée
N.B. Le choix est libre d'inclure ou pas dans les unités lexicales, les \n qui séparent ces unités.
Analyse lexicale avec super-état
Modifier l'analyseur avec 2 super-états (HEAD, CORPS) pour réaliser la même analyse lexicale.
Pour chaque champs-entête, on imprimera son nom et la taille de son contenu. Pour le corps, on imprimera la taille de son contenu.
Rapport synthétique
Modifier l'analyseur pour imprimer pour chaque champs d'entête et pour le corps de message le nombre de caractères, le nombre de mots et le nombre de lignes correspondant. La vérification de la syntaxe pourra être oubliée dans cette partie.
Kabbale (JFlex seul ou autre outil)
Quel est le secret ?
Cela ressemble à des expressions régulières sur l'alphabet Σ={0,1}. Peut être que cela reconnaît des nombres à partir de leur représentation binaire ?
Utiliser l'outil JFlex pour :
- Obtenir et dessiner l'automate fini (déterministe et optimal) de chaque expression. Utiliser pour cela l'option --dump de JFlex (ou l'option --dot si elle n'est pas buguée !). Indication : les 3 automates ont 3 états et sont très semblables.
- Valider le fait que les 3 langages reconnus sont disjoints et que la réunion des 3 langages est le langage Σ*. Les 3 expressions forment une partition disjointe de l'ensemble des chaînes binaires.
- Tester la reconnaissance des 3 expressions (simultanées) sur les nombres de 1 à N écrits en binaire.
- Conclure : quel calcul est réalisée par l'automate ?
- Bonus : expliquer comment l'exercice a été construit, c'est à dire comment à partir du calcul réalisé, on peut facilement construire l'automate, et ensuite construire moins facilement mais mécaniquement les expressions régulières.
Variante de la même question
Parole de YHWH sur le mont Sinaï :
L'alphabet sont les chiffres de 0 à 9. Que calculent ces 3 expressions pour un nombre écrit en notation décimal ?
Analyseur lexical manuel (sans JFlex)
Prise en main
Analyser les sources fournies, identifier les catégories lexicales reconnues par l'analyseur et tester le fonctionnement (javac *.java; java NatLex0; java NatLex0 testfile).
Bart tue un chasseur
Compléter l'analyseur pour reconnaître les catégories :
- POINT : .
- ARTICLE : le, un.
- NOM_C : lapin, chasseur, gnou.
- NOM_P : Bart, Jeannot, Obi-Wan.
- VERBE : tue, mange.
- La catégorie MOT peut être conservée pour les mots qui n'appartiennent pas aux autres catégories.
- La catégorie NOM_P peut aussi être définie comme les MOT commençant par une majuscule.
Premiers pas CUP sans JFlex (CUP sans JFlex)
On donne aussi une spécification CUP Nat0.cup pour produire un analyseur syntaxique qui utilise l'analyseur NatLex0 au niveau lexical.
Exécuter l'analyse syntaxique
Analyser le code de la spécification CUP ; Générer l'analyseur syntaxique ; et Tester l'analyseur :
Exécuter correctement l'analyse syntaxique
Modifier l'analyseur lexical NatLex0 et la génération avec l'outil CUP pour obtenir une exécution correcte. Utiliser java -jar $LIBCOMPIL/lib/java-cup.jar -interface Nat0.cup ## ou cup -interface Nat0.cup pour produire l'interface sym.java contenant la définition des catégories lexicales par CUP.
Intégrer cette définition dans la définition de la classe NatLex0.java avec implements sym Tester que l'analyseur syntaxique accepte maintenant toutes séquence de mots suivies d'une fin de fichier.
Bart mange le lapin. le lapin tue un chasseur.
En reprenant le corrigé de l'exercice précédent pour le niveau lexical, et en complétant l'analyseur syntaxique Nat0.cup, produire un analyseur syntaxique pour la grammaire "langage Naturel Simple" des diapositives du cours.
Compléter la grammaire pour accepter une séquence de phrases.
Compléter enfin pour avoir une reprise sur erreur en cas de phrases incorrectes (utilisation du token error pour la resynchronisation sur POINT)
Pierre, Papier,... (Bonus)
Étendre l'analyseur pour accepter les énoncés possibles d'un jeu "Pierre, papier, ciseaux, lézard, Spock".
Premiers pas CUP et JFlex (JFlex + CUP)
- Créer un projet CUP+JFlex ($ Compil-new-cup mon_projet) et aller dans le projet.
- Analyser les fichiers fournis et tester le fonctionnement sur spec/sample.
- Intégrer dans le dossier spec les squelettes de spécification et
- Tester l'analyseur.
- Compléter les deux spécifications pour obtenir l'analyseur de l'exercice précédent.
Addition selon Turing (JFlex+CUP)
L0 est algébrique ?
Prouver que ce langage est algébrique déterministe ! (Oups ! de la théorie !).
En pratique, construire une spécification CUP sans conflits qui reconnaît ce langage. Le langage est alors algébrique puisque décrit par une grammaire context-free, et déterministe puisque reconnaissable sans conflits par CUP.
On peut utiliser les spécifications suivantes pour l'analyse ligne à ligne d'un langage sur {a, b, c}*. Pour l'exercice, il convient juste de modifier la définition du symbole l0 dans la spécification CUP.
Variations
Même question pour :
Piège
Même question pour :
Hotelterminus, 1ère légion, 3ème cohorte, 2ème manipule, 1ère centurie (JFlex+CUP)
- Tester cet analyseur en mode interactif ou avec la classe romGen.
- Ajouter des valeurs sémantiques et des actions sémantiques dans la spécification CUP, pour que l'analyseur réalise et imprime la conversion décimale de chaque nombre romain correct. Aucun besoin de modifier la grammaire.
Calculatrice Logique (JFlex+CUP)
(source Michel Meynard)
L'objectif de cet exercice est d'écrire une calculette capable de reconnaître et d'évaluer des expressions logiques d'ordre 0.
De manière similaire aux expressions arithmétiques, les expressions logiques d'ordre 0 sont construites à partir des composants suivants :
- Constantes : 0 ou false ou faux et 1 ou true ou vrai.
- Opérateurs binaires : conjonction & ou et ou and, disjonction | ou or ou ou, implication =>, équivalence <=>, et le OU exclusif ^.
- Opérateur unaire : négation ! ou not ou non.
- Parenthèses : ( et ).
Les expressions logiques sont évaluées de gauche à droite. L'ordre de priorité des opérateurs est : {|, =>, <=>, ^} << & << !. Les associativités droites ou gauches des opérateurs sont à préciser.
Pour la lisibilité des expressions, on ajoutera :
- Écriture ligne à ligne : une expression est écrite sur une même ligne et on a au plus une expression par ligne.
- Espaces : les espaces ou les tabulations sont possibles et sans effet.
- Commentaires : tout texte commençant par # et se terminant à la fin de la même ligne est sans effet.
Exemples :
Calculatrice Logique
Écrire un analyseur syntaxique qui évalue (imprime VRAI ou FAUX) des expressions logiques d'ordre 0 écrites ligne à ligne.
Calculatrice Logique avec variables et controle d'erreur
Ajouter à cette calculette la fonctionnalité suivante :
- Utilisation de variables avec une table de symbole rudimentaire pour conserver le résultat de calculs précédents.
- L'affectation et l'utilisation de ces variables ressemblera à la syntaxe C ; par exemple a = 0 | 1 => 0 puis b = a => (0|1).
- Initialisation par défaut des variables à Faux.
- Ajouter enfin le traitement des erreurs de syntaxe (ligne incorrecte) et sémantique (variable non initialisée).
Calculatrice Ensembliste (JFlex+CUP)
- Constantes : {} (ensemble vide), {i} (singleton), ou de façon générale {i, j, k,... } avec i, j, k... des valeurs entières. L'ordre des éléments ou l'unicité des éléments est indifférent.
- 3 Opérations ensemblistes : Union, Intersection, Différence. On utilise les mots clés : union, inter, diff.
- Nom et Affectation de Variables.
- Des parenthèses : ( et ).
- Écriture ligne à ligne : une expression est écrite sur une même ligne et on a au plus une expression par ligne.
- Blancs : les espaces ou les tabulations sont possibles et sans effet.
- Commentaires : tout texte commençant par # et se terminant à la fin de la même ligne est sans effet.
Calculatrice ensembliste avec notation opérateur
Les opérations sont écrites sous forme d'opérateurs en notation infixe et les parenthèses servent à gérer l'ambigüité et la priorité entre les opérateurs. N.B. : union et inter sont totalement associatifs et inter est usuellement prioritaire sur union. Écrire l'interpréteur ligne à ligne pour les expressions ensemblistes. Utiliser la classe Java HashSet avec les méthodes add(),remove(),addAll(),removeAll,retainAll()
Calculatrice ensembliste avec notation fonctionnelle (varargs)
Ajouter dans l'interpréteur précédent la reconnaissance des opérations ensemblistes avec une notation fonctionnelle union(xxx, yyy,...). Les "fonctions" union et inter ont un nombre d'arguments quelconque non nul, la fonction diff a 2 arguments.
Calculatrice Vectorielle (JFlex+CUP)
- Constantes Scalaires : des valeurs entières signées selon la notation usuelle.
- Constantes Vecteurs : un vecteur contient un nombre fini de composantes scalaires, il sera noté entre crochets [ ], avec une virgule , entre chaque composante scalaire. Ex : [3,-2,4,5] ou [2,1].
- Les composantes d'un vecteur peuvent être des expressions Scalaires.
- Le vecteur vide à zéro composante noté [].
- L'opérateur noté + qui réalise l'addition usuelle de valeurs scalaires.
- L'opérateur noté + qui réalise l'addition de 2 vecteurs. L'addition suppose que les vecteurs soient de même taille, l'addition se fait alors composante par composante. Ex : [3,5,7]+[1,-2,-5]==[4,3,2].
- L'opérateur noté * qui réalise la multiplication usuelle de valeurs scalaires.
- L'opérateur noté * qui réalise la multiplication d'un vecteur et d'un scalaire. On autorise la multiplication dans les 2 sens. Ex : 4*[1,2,3]==[1,2,3]*4==[4,8,12].
- L'opérateur noté . qui réalise le produit scalaire de deux vecteurs de même taille. Ex : [1,2].[1,2]==5.
- La fonction dim(...) qui prend en argument une expression vectorielle et retourne le nombre de composantes du vecteur. Ex : dim([])==0 , dim([1,3])==2.
- Des parenthèses ( et ) pour imposer l'ordre d'évaluation des opérateurs.
- On définira les règles d'associativité et de priorité selon les "usages courants".
- Écriture ligne à ligne : une expression est écrite sur une même ligne et on a au plus une expression par ligne.
- Blancs : les espaces ou les tabulations sont possibles et sans effet.
- Commentaires : tout texte commençant par # et se terminant à la fin de la même ligne est sans effet.
Calculatrice scalaire et vectorielle
Écrire l'interpréteur ligne à ligne pour les expressions scalaires et vectorielles. Chaque ligne correcte contient une expression scalaire ou une expression vectorielle dont on imprime la valeur. On prendra soin de signaler les erreurs lexicales (i.e. caractère invalide), les erreurs syntaxiques (i.e. vect*vect), et les erreurs sémantiques (i.e. tailles de vecteurs non compatibles). Utiliser la classe ArrayList avec le constructeur new java.util.ArrayList<>() et les méthodes add(Integer i) et size().
Variations (Bonus)
Quelques extensions ouvertes :
- Ajouter des matrices définies comme vecteur de vecteur. On peut définir des vecteurs "horizontaux" avec [ ] et des vecteurs "verticaux" avec { } et avoir 2 écritures pour une même matrice ({[1,2,3],[3,4,5]} == [{1,3},{2,4},{3,5}])
- Ajouter des variables dans la calculatrice. Ces variables doivent être typées pour différentier les expressions de type scalaire ou de type vecteur. Pour simplifier, on peut décider d'avoir des noms de variable séparées au niveau lexical pour réaliser le typage implicite (i.e noms S* et V*)...
- Ajouter d'autres opérations : produit vectoriel, fonction Norme, projection, vecteur unitaire,...
- ...
Analyse syntaxique LL manuelle (sans JFlex et sans CUP !)
- Le lookahead de 1 est réalisé par la méthode Tok aheadTok().
- les méthodes LireX() pour les symboles terminaux X sont réalisées sous la forme LireTok(Tok.X).
CSC4251-52 (CSC 4536), TELECOM SudParis, P. Hennequin,Last modified: Juillet 2022

