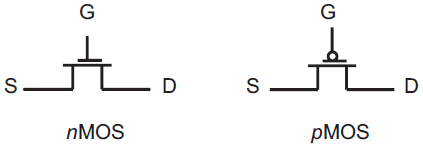From the transistor to the processor
In this lab, we suppose that we are stuck on a totally useless desert island. Since we have a crazy urge to play pacman, we decide to build a small processor to entertain our time. For that, fortunatly, we have an old electric generator and a box with many transistors and wires.
Terminating the whole processor takes roughly twelve ours, which means roughly six hours of personnal work. We hope you will have as much fun as your teachers in completing this processor!
If you need help, you can take a look at the final version of the processor here.
From transistors to NAND gates
To begin, we will study how we can design a NAND gate by starting from a transistor.
In the exercise, we consider MOS (Metal-Oxide-Semiconductor) transistors. MOS transistors are commonly used to build processors. There are two types of MOS transistors: the nMOS transistors and the pMOS transistors. Since current processors use both types of MOS transistors, we say that the current processors use the CMOS (Complementary Metal-Oxide-Semiconductor) technology.
As shown in Figure , a MOS transistor is a hardware component with three entries: S (source), G (grid) and D (drain). A MOS transistor behaves as a switch, in which the switch is controlled by electricity. When we power G, we connect S to D in a nMOS transistor, whereas we disconnect S from D in a pMOS transistor. We can also illustrate the behavior of a transistor by considering a river that flows from S to D. G acts as a dam: when we power G, we add a dam between S and D in a pMOS transistor, whereas we remove the dam in a nMOS transistor.
|
|
|
||||||||||||||||||||||
.aThe NAND gate (credit wikipedia). |
.bTruth table of the NAND gate. |
||||||||||||||||||||||
CMOS transistors are at the basis of the logic gates. Figure .a shows how we can build a NAND (NOT AND) gate from CMOS transistors. In the figure, Vdd refers to the positive voltage and Vss to the negative voltage (zero Volt). We say that Vdd is equal to 1 (true), and that Vss is equal to 0 (false). Figure .b recalls the truth table of a NAND gate. For the A or B inputs, 1 (resp. 0) means that we apply a power of Vdd (resp. Vss) to the input.
Explain why Figure .a implements a NAND gate.
From NAND gates to other logic gates
The NAND gate is what we call a universal gate: we can build any logic gate from a NAND gate. In this exercise, we will leverage this property to build the most common gates (NOT, OR, NOR, AND, XOR, XNOR).
Circuitverse
To design our logic circuits, we will use the amazing circuitverse simulator. For that, you have to open https://circuitverse.org/simulator.
In order to save your circuits, you have to create an account. For that, click on "Sign In" and then on "New user? Sign up". At this step, you can either create a new account or use your google, facebook or github account.
First circuit
In order to learn how we can use circuitverse, you will first design the very simple circuit with a NAND gate presented in Figure . For that, in the "Circuit Elements" panel, click on "Gates". Then, select the NAND gate (5th gate), which allows you to add a NAND gate on the grid. You can now add two inputs. For that, in the "Circuit Elements" panel, click on "Input". Then, select the 1st element (a square with 1 inside), which is called an Input. You can add two inputs on the left of the NAND grid on the grid.
You can see that you have a green circle on the right of an Input. This green circle is a connector. When you click on a connector, you start to create a wire. Create wires to connect your two inputs to the inputs of the NAND gate (connectors on the left). You can observe that when you click on an input, you change its value. You can also observe that the color of a wire change when the value of the input change: light green if the value is equal to 1, dark green otherwise.
Now, we will add an output. For that, in the "Circuit Elements" panel, click on "Output". Then, select the 1st element (a square with X inside), which is called an Output. Add an Output on the right of the NAND gate. Finally, creates a wire to connect the output of the NAND gate (connector on the right) to the Output. You can verify that the NAND gate actually implements the NAND truth table by playing with the values of the inputs.
Circuitverse project
Now, we will see how we can save a project. For that, you first have to give a name to your project. In the "Properties" panel, give a name to your project ("Project"). Then, in the project menu, click on "Save online". At this step, you can edit your project. You can let the project description as it is and just click on "Update Project" button.
At this step, click on your name (top right) and on "Dashboard". You should see all your projects here. You have to click on the "Launch" button of your unique project to restart the simulator. After this step, when you click on "Save online" in the "Project" menu, you stay on the simulator.
Mastering circuitverse
In order to select a single element, you just have to click on the element. For a element, you have to click inside the element (not on its connectors). When selected, the element becomes yellow. For a wire, you have to click on the wire (not on its connectors). When selected, the wire becomes blue.
In order to delete an element, you have to select it and to press the "Delete" key of your keyboard.
In order to move an element, you have to select it and to move it. Be careful, when you move a component, the wires connected to the element moves also. Deleting the wires before moving a component is often a good idea.
In order to select multiple elements, press the shift key of the keyboard, and with the mouse, you can select multiple elements. You can then delete them all or move them all.
Short circuit
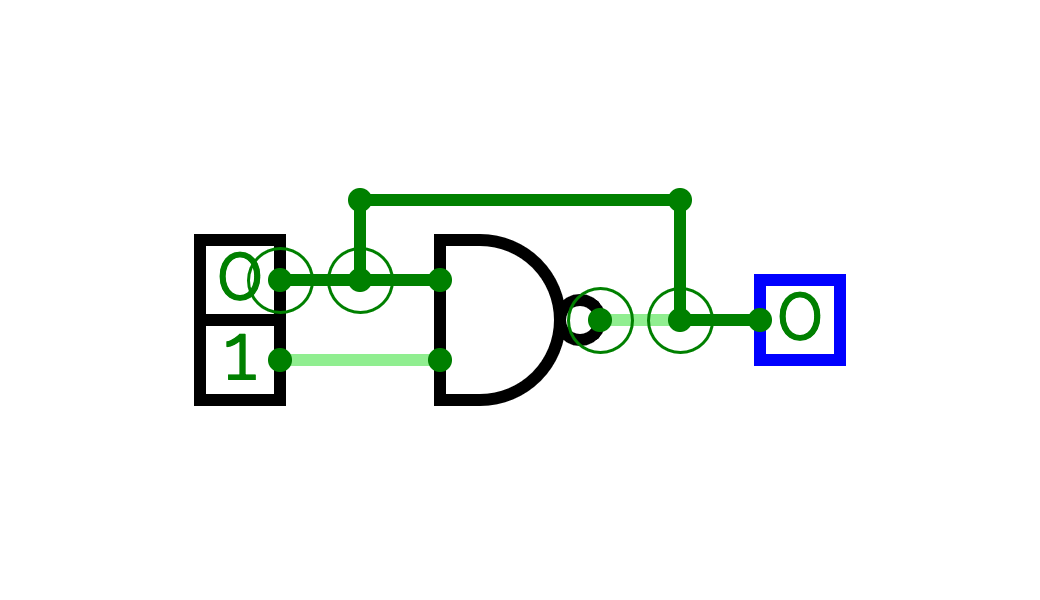
You can start a wire from any point of an existing wire. We will use this possibility to see how we can build a short circuit. A short circuit is thus buggy because a short circuit is a circuit in which you connect a 0 with a 1. In order to illustrate, we will create a short circuit from the NAND circuit. For that, you have to reproduce the circuit presented in Figure . When the short circuit is created, you should see a red messages on the bottom (Contention Error: 1 and 0 at Input and Main). If you want to see the message again, you have to change the value of the input. On the circuit, you can see where something goes wrong with the large circles around the connections that connect a 0 to a 1.
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Now that you master circuitverse, implement the common gates presented in Figure by starting only with NAND gates. As soon as you have a new gate, you can use it to implement the next gate (all the gates are available in the "Gates" menu of the "Circuit Elements" panel).
You should create the gates in this order:
- NOT Notice that NAND(A,A) = NOT(A).
- AND Notice that NOT(NAND(A,B)) = AND(A,B).
- OR Notice that OR(A,B) = NOT(AND(NOT(A),NOT(B))) = NAND(NOT(A),NOT(B)).
- NOR Notice that NOR(A,B) = NOT(OR(A,B)).
- XOR Notice that XOR(A,B) behaves as OR(A,B), except when A = 1 and B = 1. In this case, the output is 0 and not 1. From this observation, we can find that XOR(A,B) = AND(NAND(A,B),OR(A,B)).
- XNOR Notice that XNOR(A,B) = NOT(XOR(A,B)).
The adder
In this exercice, we will create our first useful circuit: the adder, which is able to add two values.
1-bit half adder
| v0 | v1 | res | cout |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
To begin, we will implement what we call the 1-bit half adder. A 1-bit half adder is able to add two bits. It takes as input v1 and v2 and returns two values: the sum res and the carry cout. Figure presents the truth table of a 1-bit half adder. The last line means "1 + 1 = 0 and I carry 1".
In circuitverse, start by deleting all the previous circuits that you have on the grid (shift + mouse to select multiple elements). Then, implement the 1-bit half adder.
You can see that :
- You can use a XOR gate to have res,
- We have a carry if and only if v0 = 1 and v1 = 1.
Layout of a circuit
In circuitverse, you can reuse a circuit to create new more complex circuits. In our case, we will reuse the 1-bit half adder to implement a 1-bit full adder. For that, we have first to name our 1-bit half adder. In order to name our 1-bit half adder, replace "Main" by "half-add" in the "Circuit:" field of the "Properties" panel.
Then, we have to give names to the input and output. For that, click on a first input and give it the name v0 by changing its "Label" in the "Properties" panel. Similarly, name the second v1. For the outputs, you have to use the names res and cout.
Finally, we have to edit the layout of the circuit. For that, click on "Edit Layout". You can move the inputs and outputs by clicking on the connectors. You can also change the size of the circuit by playing with the "Width" and "Height" in the "Layout" panel. You can finally move the title by playing with the arrows below "Title". When you think that your layout is satisfactory, you just have to click on "Save" in the "Layout" panel to come back to the circuit.
1-bit full adder
We will now reuse our half-add to implement a 1-bit adder. We will call this circuit 1-add. In order to create a new circuit, click on the "+" on the right of "half-add" below the menu bar. You have to give the name "1-add" to your circuit.
In 1-add, add three inputs named v0, v1 and cin (carry of the previous step, see the next questions). Add also two outputs named res and cout. Finally, reuse half-add circuits (menu Circuit->Insert SubCircuit) to implement a 1-add circuit. This circuit generates the sum of v0, v1 and cin in res, and generates the carry of the sum in cout.
For the sum, you have to use two hald-add circuits. For the carry, as soon as one of the half-add has a carry, 1-add has a carry. In other words, cout = or(cout first half-add, cout second half-add).4-add
Now that we are able to add two bits, we can build a more complex adder for 4-bit values. For that, create a new circuit named 4-add. Then, create an input named v0. In order to use 4-bit inputs, click on v0. On the "Properties" panel, change the "BitWidth" to 4. Your input should now be a 4-bit value. Create also a 4-bit input v1 and 1-bit input cin.
Now, we will split our inputs into multiple bits. For that, click on "Misc" in the "Circuit Elements" panel. Select the third elements, which is called a splitter. When you click on the splitter, you first have to give the number of bits that you want to split: "4" in our case. Then, you have to give the decomposition that you want: "1 1 1 1" in our case since we will have to handle each bit individually. To illustrate how decomposition works, if you want to decompose you 4-bit value into a value of 3 bits and one of 1 bit, you have to write "3 1".
Connect a splitter to v0 and a splitter to v1. Now, you can chain four 1-add to compute the sum of your 4-bit inputs.
You have to connect cin to the cin of the first 1-add, and then to connect the cout of 1-add to the cin of the next 1-add.Now, we will create the outputs: res is a 4-bit output and cout is the carry of the last 1-add. In order to aggregate the outputs of the four 1-add, we also need a splitter that splits a 4-bit values into four 1-bit values. To connect this splitter to res, you have to reverse it. For that, click on the splitter, and then, on the "Properties" panel, change the direction to use "Left" instead of "Right".
The multiplexer
In this exercise, we will design a useful circuit: the multiplexer. A multiplexer takes as input values and a selector, and, based on the selector, outputs one of the values. This circuit implements thus a kind of if/then/else or switch.
1-bit multiplexer with a 1-bit selector
To begin, implement the 1-1-mux multiplexer. This multiplexer takes as input two 1-bit values named x0 and x1 and one 1-bit value named sel. When sel = 0, the circuit outputs x0, otherwise, it outputs x1.
The circuit outputs OR(AND(x0, NOT(sel)), AND(x1, sel)).2-bit multiplexer with a 1-bit selector
Now, implement a circuit named 1-2-mux. This circuit uses splitters and 1-1-mux circuits to implement a multiplexer that takes as input two 2-bit values named x0 and x1 and 1-bit value name sel. The circuit output x0 if sel = 0 and x1 otherwise.
2-bit multiplexer with a 2-bit selector
We will now implement a multiplexer that takes four 2-bit values named x0, x1, x2 and x3. It takes also as input a 2-bit selector named sel. The circuit outputs x0 when sel = 0, x1 when sel = 1, x2 when sel = 2 and x3 when sel = 3.
You have to reuse three 1-2-mux circuits. The first 1-2-mux is used with x0, x1 and the first bit of sel to select either x0 or x1. The second 1-2-mux is used with x2, x3 and the first bit of sel to select either x2 or x3. Finally, the last 1-2-mux is used with the outputs of the two other 1-2-mux circuits and the second bit of sel to select the final output.Modulo 5
Now that you understand the principle, instead of creating other multiplexers with larger input values or larger selectors, we will reuse the multiplexers provided by circuitverse. We will show how we can reuse the multiplexers of circuitverse by designing a circuit named mod5. We will use mod5 later to build the processor. This circuit performs a modulo 5 on a 4-bit value. Technically, mod5 takes as input a 4-bit value named in and output a 4-bit value named out.
- When in is equal to 0, 1, 2, 3 or 4, out = in.
- When in is equal to 5, out = 0.
- When in has a different value, any output value is correct.
In order to implement the circuit, you have thus to output 0 if the bit 0 and 2 of in are equal to 1, and to output in otherwise. For that, you have to use a multiplexer. This multiplexer takes 4-bit values as input and uses a 1-bit selector. You can find a multiplexer in the "Decoder and Plexers" menu of the "Circuit Elements" panel. The multiplexer is the first circuit. You can configure the multiplexer by modifying its Properties: "BitWidth" gives the size of the input value and "Control Signal Size" gives the size of the selector.
You will also have to generate a 4-bit constant value of 0 when in is equal to 5. For that, you have to use the 5th input (a square with a 0) in the "Circuit Elements" panel. By default, the constant is a 1-bit value equal to 0. You can change the value of the constant by double clicking on it. If you write 0000, the value becomes a 4-bit value equal to 0.
Implement the mod5 circuit. You should use a splitter, a 4x1 multiplexer, a 4-bit constant 0 and a AND gate.
Arithmetic and Logical Unit
In this exercice, we show how we can design an Arithmetic and Logical Unit (ALU). An ALU takes as input two values and a function number. The function number gives the operation that the ALU has to execute: an addition, a subtraction, a logical operation, a bit shift etc.
In our processor, we only need a very simple ALU able to perform addition. Our ALU outputs a single 8-bit value named R (result). It takes as input two 8-bit inputs named A and D, and a 2-bit function named fun. When fun is equal to 0, R = A + D. Otherwise, R = 0. In order to select the output, you have to use a multiplexer. This multiplexer takes as input 8-bit values and a 2-bit selector. When the selector (fun) is equal to 0, it selects the output of an adder. Otherwise, it selects a 8-bit constant value equal to 0.
A simple ALU
Implement our simple ALU. To perform the addition, you have to reuse the adder provided by circuitverse. You can find it in the "Misc" menu of the "Circuit Elements" panel. The adder is the first circuit. If you move your mouse on top of one of the connector of the adder, you can see the name of the connector:
- A and B are the input values,
- Cin is the input carry (constant 0 in our circuit),
- Sum is the result,
- Cout is the output carry (not used in our circuit).
The register
In this exercise, we will design step by step a register. A register is a kind of variable inside a processor since a register is a circuit able to "memorize" a value.
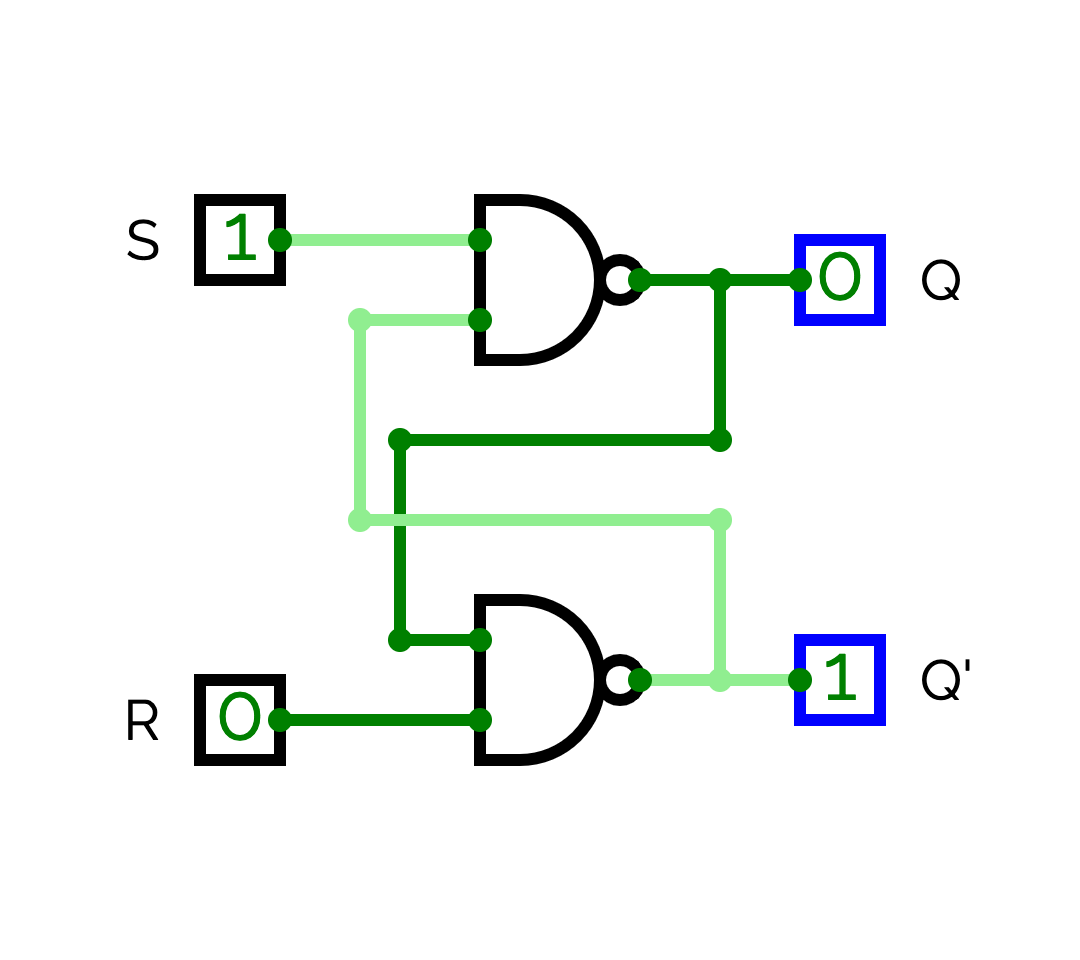
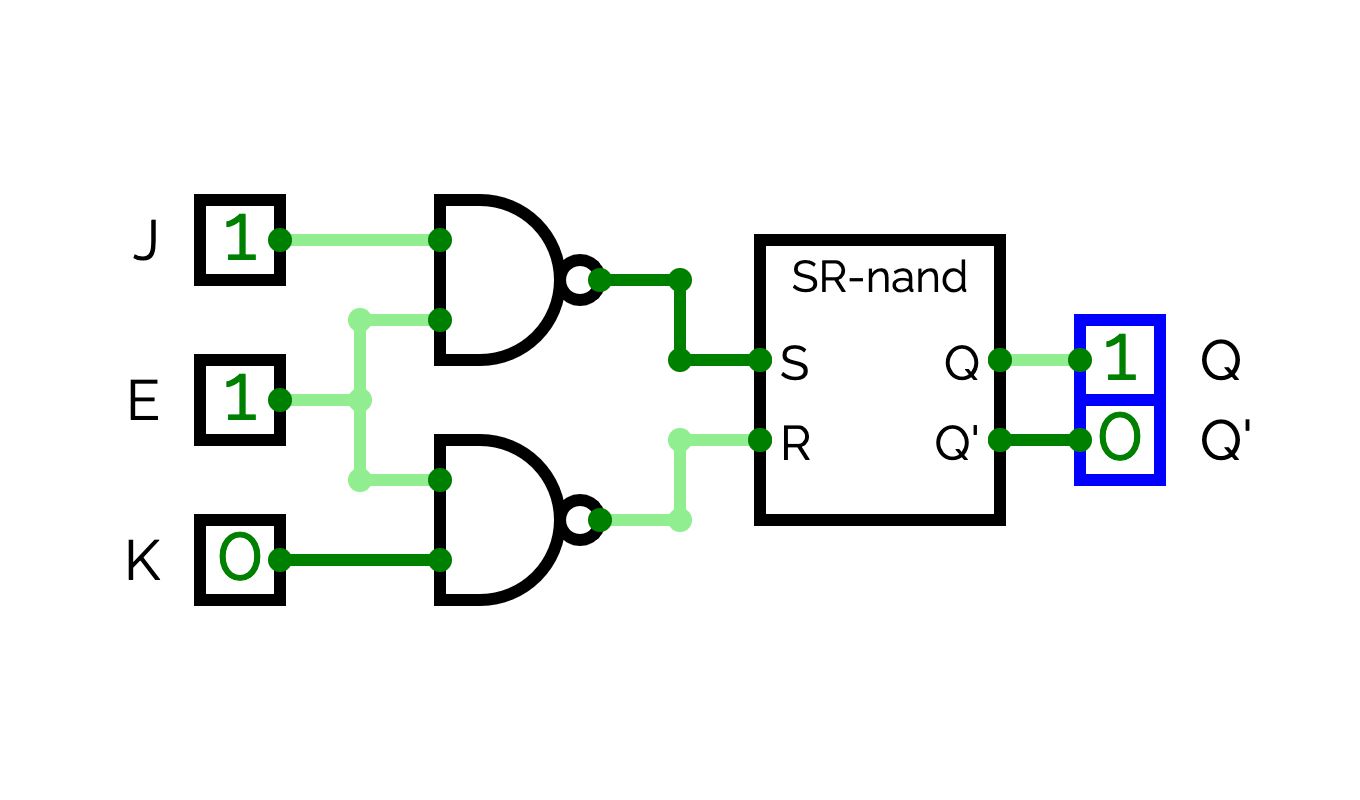
SR-nand (1/3)
SR-nand (2/3)
In which state are Q and Q' when S = 0 et R = 1? And when S = 1 and R = 0?
SR-nand (3/3)
We now suppose that S = 0 and R = 1. What are the states of Q and Q' when S becomes equal to 1? To understand the states of Q and Q', you have to exhaustively study the case where the top NAND gate propagates the result first and the case where the bottom NAND gate propagates the result first. Similarly, if we suppose that initially, S = 1 and R = 0, what are the states of Q and Q' when Q becomes equal to 1?
The JK flip-flop (1/3)
As shown in the previous question, when S = 1 and R = 1, we can have two different output values:
- Q = 1 and Q' = 0 if we come from the state S = 0 and R = 1,
- Q = 0 and Q' = 1 if we come from the state S = 1 and R = 0.
This property means that we can memorize the output of the circuit at 0/1 or 1/0 when S = 1 and R = 1. The JK flip-flop circuit leverages this property to implement a kind of memory. The name JK seems to come from the inventor of this circuit (Jack Kilby).
In a new circuit named JF-flip-flop, reproduce the circuit presented in Figure .
The JK flip-flop - copy of the input value (2/3)
We start by studying how the circuit behaves when E (enable) is equal 1. If we suppose that K is always the invert of J, why the circuit copies the input J into Q and the input K into Q'? In other words, why J = 1 and K = 0 => Q = 1 and Q' = 0, and why J = 0 and K = 1 => Q = 0 and Q' = 1?
The JK flip-flop - memorize the value (3/3)
Now, we will show that when E becomes equal to 0, the JK flip-flop blocks the output of the circuit in its previous state.
For that, we first suppose study the case where, initially, J = 1, K = 0 and E = 1. If you switch E to 0 from this state, what is the output of the circuit? Why Q and Q' do not change if you modify J or K?
Similarly, we suppose that initially J = 0, K = 1 and E = 0. If you switch E to 0, what is the output of the circuit? Why Q and Q' do not change if you modify J or K?
Half D flip-flop
We will now leverage the JK flip-flop to build a new circuit named half-D-flip-flop. A half-D-flip-flop has two inputs: a 1-bit input named D (data) and a 1-bit input named E (enable). The half-D-flip-flop has two 1-bit outputs Q and Q'. When E = 1, the circuit has to copy D in Q, and to copy the invert of D in Q'. When E = 0, the circuit has to output the value memorized when E = 0. In this case, if we change D, the values of Q or Q' should not change.
Implement the half-D-flip-flop circuit.
In order to implement half-D-flip-flop, you simple has to connect the E input of half-D-flip-flop to the E input of a JK-flip-flop, D to the J input of the JK-flip-flop, and the invert of D to the K input of the JK-flip-flop.First version of the D-flip-flop
A register is roughly a half-D-flip-flop in which we connect E to a clock. A clock is a source that regularly switches between 0 and 1. As is, the circuit output the memorized value when clock is equal to 0, and record a new value when clock is equal to 1. When clock switch from 0 to 1 and then from 1 to 0, we say that the processor executes a whole cycle.
This simple circuit is, however, not yet usable. Technically, imagine a circuit that executes something like %r1 = %r1 + 1, where %r1 is a 8-bit half-D-flip-flop able to memorize 8 bits. Initially, %r1 and clock are equal to 0. To compute the value %r1 + 1, we will connect the output Q of %r1 to the input A of an adder. For the input B of the adder, we will use the constant 1. The result of the adder is thus %r1 + 1. We just have to connect this result to the input D of the half-D-flip-flop to compute %r1 = %r1 + 1. However, this circuit behaves incorrectly: when clock switch from 0 to 1, we memorize the new value %r1 = 0 + 1. But changing D immediately changes %r1, which becomes equal to 1. The adder will thus output 2, which will be used as the new D input. As a result, %r1 will increment quickly while clock = 1. This is not what we want: we want to stabilize the value of %r1.
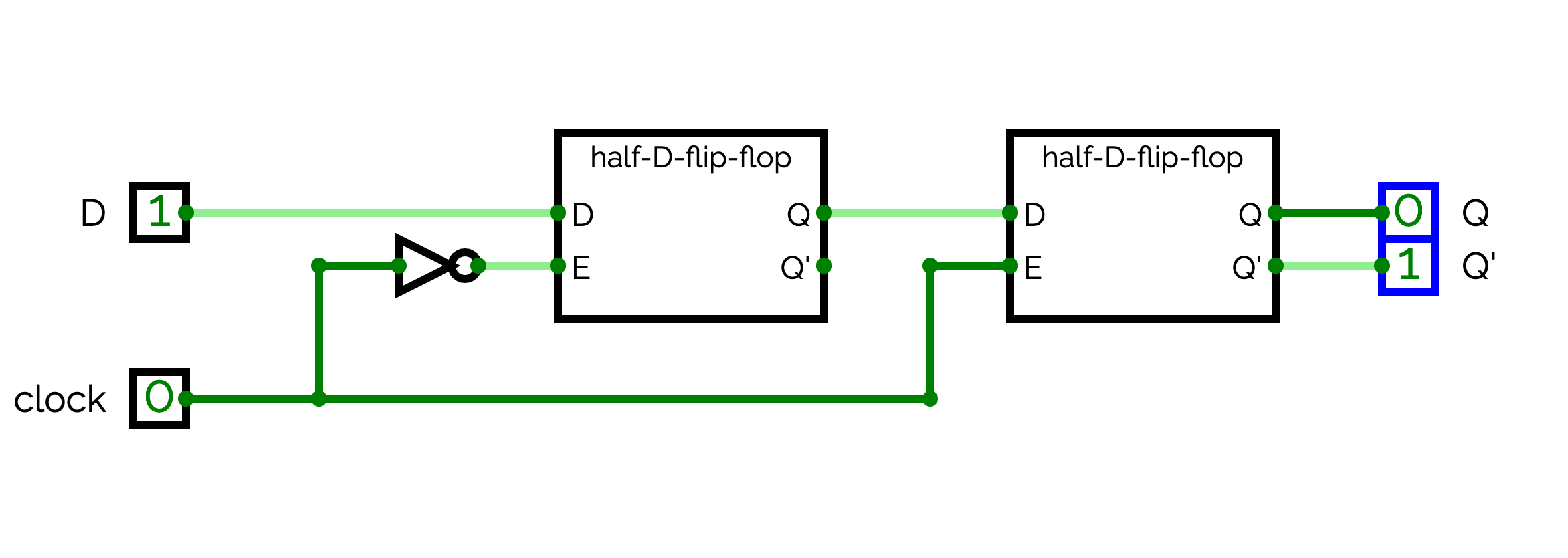
To stabilize the result of a register, we have to use two half-D-flip-flop as shown in Figure . The half-D-flip-flop on the left is called the master and the half-D-flip-flop on the right the slave. The invert of clock is connected to the master whereas clock is directly connected to the slave. When clock = 0, we are in what we call the memorization phase. The master memorize the input D, but the slave still output the previous memorized value. When clock = 1, we are in what we call the computation phase. The master outputs the memorized value to the slave. The slave memorizes the new value and outputs it. This value can be used to compute a new value, for example, %r1 = %r1 + 1. During this phase, even if D change, the master does not yet record the new computed value, which stabilizes the register. The new computed value is only memorized in the master when clock switches from 1 to 0.
In a circuit named D-flip-flop, implements the circuit presented in Figure . By playing with D and clock, verify that we actually have a computation and a memorization phase.
The complete D flip-flop
We will now design a complete D flip-flop. A D flip-flop implements 1-bit register. In your D-flip-flop circuit, additionally to the D and clock outputs, adds the following inputs:
- preset: the initial value of the register,
- reset: when reset = 1, both the master and the slave memorize immediately preset,
- E: when E = 1, the register memorizes new values when clock change, otherwise, it does not memorize new values.
In the remainder of the lab, we will use preset/reset to reinitialize our processor. We will use E to block a register. Typically, we will use E to select which register is modified during a cycle. If we imagine a processor with 3 registers %r0, %r1 and %r2, in order to execute %r1 = %r1 + 1, we will have to set the E input of %r0 and %r2 to 0 to block them, and the E input of %r1 to record the new value of %r1.
The D input of the master is equal to D if reset = 0 and preset of reset = 1.
The E input of the master and the slave are equal to 1 when reset = 1. Otherwise, if E is equal to 0, the E input of the master of the slave are equal to 0. Otherwise, the E of the master is equal to the invert of clock and the E of the slave is equal to clock.
In other words:
- The E of the master is equal to OR(reset, AND(E, NOT(clock))),
- The E of the slave is equal to OR(reset, AND(E, clock)).
The counter processor
We will now design our first processor, which increments a counter at each cycle. We will reuse this processor later when we will design the complete processor.
The register
Create a new circuit named COUNTER. In this circuit, add a register (a D- flip-flop) by selecting the 1st element of the "Sequential Elements" of the "Circuit Elements" panel. We will use 4-bit values. Modify the "BitWidth" accordingly field of the "Properties" of the register.
Connect also the entries at the bottom of the register to:
- a 1-bit constant 1 to the Enable input of the register (left connector),
- a 4-bit value 0000 to the Preset input of the register (middle connector),
- a 1-bit input named reset to the Asynchronous Reset input of the register (right connector).
Finally, we will connect automatic clock to the Clock input of the register (connector at the bottom on the left). The automatic clock is the 8th element of the "Sequential Elements" of the "Circuit Elements" panel.
Finally, add a 4-bit input named value connected to the D connector at the top on the left. At each cycle, your circuit should copy the value of this input in the register.
First counter
Now, add a 4-bit adder to your circuit. Connect a 4-bit constant 0001 to the A entry of the adder (left, top) and the Q output of the register (right, top) to the B entry of the adder (left, middle). Finally, connect a 1-bit constant 0 to the Cin entry of the adder. Remove the value entry and connect the output Sum of the adder (right, middle) to the D entry of the register. When reset is off, you should see the register incremented at each cycle.
Counter from 0 to 4
Now, we want a counter that restarts at 0 when the value reaches 5. For that, you have to reuse the mod5 circuit implemented in a previous exercise.
Demultiplexer
In order to design a processor with multiple registers, we have to activate the E input of the output register of an instruction. For example, in order to execute %r2 = %r1 + 1 in a processor with 4 registers, we have to activate the E input of the register %r2, but not the E input of the register %r1. To select an output, we will use a demultiplexer. A demultiplexer has two inputs:
- value: a n-bit input value,
- sel: a k-bit selector.
A demultiplexer has m = 2k outputs named x
1-1-demux
We will start by implementing a demultiplexer with a value encoded with 1 bit and a selector encoded with 1 bit.
With a 1-bit selector, the demultiplexer has two outputs x
Implement this multiplexer in circuit named 1-1-demux.
- If sel = 0, then x
0 = value and x1 = 0, - If sel = 1, then x
1 = 0 and x1 = value.
In other words:
- x
0 = 1 if value = 1 and sel = 0. Otherwise, x0 = 0, - x
1 = 1 if value = 1 and sel = 1. Otherwise, x1 = 0.
2-1-demux
We will now implement a demultiplexer with a 1-bit value and 2-bit selector.
This demultiplexer has four outputs: x
In general, in order to build a (n+1)-1-demux from two n-1-demux, we observe that we have to split the n first bits of sel from the last bit. We have to use these n bits as a selector for the two n-1-demux. The first n-1-demux is connected to the first set of outputs (from 0 to 2n - 1) and the second n-1-demux to the second set of outputs (from 2n to 2n+1 - 1). If the bit n+1 of sel is equal to 0, we have to send value to the first n-1-demux and 0 to the second n-1-demux. If the bit n+1 of sel is equal to 1, we have to send O to the first n-1-demux and value to the second n-1-demux.
In details:
- The input of the first n-1-demux is equal to 1 if and only if value is equal to 1 and the bit n+1 of the selector is equal to 0,
- The input of the second n-1-demux is equal to 1 if and only if value is equal to 1 and the bit n+1 of the selector is equal to 1.
You can observe that we are just reusing the formula that we used for the 1-1-demux.
The processor
In this exercise, we will design a complete 8-bit processor step by step.
The REGS circuit
Our processor uses 8 8-bit registers. They are indexed from 0 to 7. They are named %r0, %r1, %r2, %r3, %r4, %insnl (index 5), %insnh (index 6) and %pc (index 7). The registers %insnl and %insnh are used to store the current instruction inside the processor. We use two registers because we need 16 bits to encode an instruction. The register %pc is the program counter: it contains the address in memory of the next instruction.
In order to hide the complexity of managing 8 registers, we will design a circuit named REGS in this exercice. REGS has 7 inputs:
- 3-bit sA (selector for A): gives the index of the first register used as input by the current instruction,
- 3-bit sD (selector for D): gives the index of the second register used as input by the current instruction,
- 1-bit wr (write register): when equal to 1, the current instruction writes in a register, other the current instruction does not,
- 3-bit sR (selector for the result): gives the index of the register modified by the current instruction when wr = 1,
- 8-bit R (result): give the result of the current instruction, which has to be written in rsel when wr = 1,
- clock: the clock,
- reset: used to reset the 8 registers to their initial value (0).
Typically, when the processor executes %r3 = %r2 + %r1, sA = 1, sD = 2, sR = 3 and wr = 1. If we suppose that the result of %r2 + %r1 is 12, R will be equal to 12. When clock will switch from 0 to 1 and from 1 to 0, the register %r3 will memorize this value.
The circuit REGS outputs 10 values:
- A: the value of the register at index sA,
- D: the value of the register at index sD,
- %r0, %r1, %r2, %r3, %r4, %insnl, %insnh, %pc: the value of each register. We will mostly use these outputs to debug our processor.
In order to write R in sR, you have to use a 3-1-demux (second element of "Decoders and Plexers" in the "Circuit Elements" panel): 3-bit selector and 1-bit input value.
The connector on the left gives the value copied into one of the x
In order to select the sA and sD registers, you have to use two 3-8-mux: 3-bit selector and 8-bit input values
The CLOCK circuit
We will now design a circuit named CLOCK. This circuit will be useful to debug the processor. The basic idea of CLOCK is that it provides a convenient interface to (i) suspend the automatic clock and (ii) execute step-by-step the processor. CLOCK has two entries:
- pause: suspend the automatic clock, which allows step-by-step execution,
- step: execute manually a clock step.
The CLOCK circuit outputs the clock. To simplify the integration of the final processor, CLOCK outputs clock twice.
Internally, CLOCK has an automatic clock (8th element of the "Sequential Elements" menu of the "Circuit Elements" panel). When pause = 0, CLOCK outputs this clock. When pause = 1, it outputs step.
Implement the CLOCK circuit. Be careful, when step = 1 and pause = 0, CLOCK has to output the automatic clock, not 1.
First components
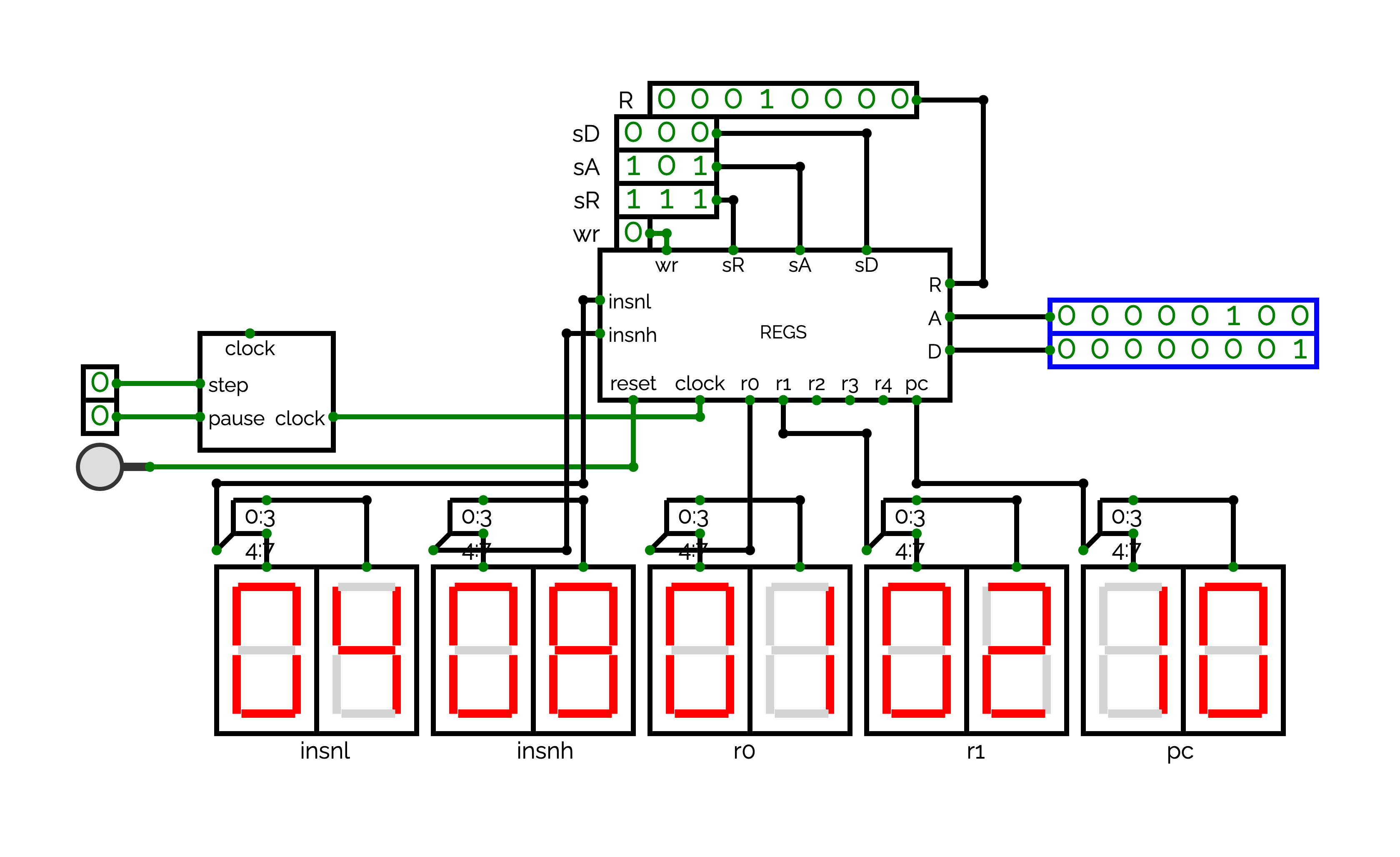
We will now start the design of the final processor in a circuit named CPU. For the moment, we will only use CLOCK and REGS. Organizing the grid of CPU will become complex when we will add new circuits. For this reason, Figure presents how you can places CLOCK and REGS with "Hex Display" outputs (5th element of "Output" in the "Circuit Elements") to show the state of the registers used after in the exercise (%r0, %r1, %insnl, %insnh and %pc). Using a similar placement with similar connector positions should ease the integration.
Reproduce the circuit presented in Figure . By playing with wr, sR, and R, verify that you can actually change the values of the %r0, %r1, %insnl, %insnh and %pc. Verify also that you can see the values of the sA and sD registers in A and D.
The MINI-PC circuit
Internally, the processor will execute an instruction in 5 cycles:
- Cycle 0: load the low part of the instruction pointed by %pc in %insnl,
- Cycle 1: increment %pc,
- Cycle 2: load the high part of the instruction pointed by %pc in %insnh,
- Cycle 3: increment %pc,
- Cycle 4: execute the instruction %insnl/%insnh.
The processor thus runs an infinite loop that executes these 5 cycles. In order to run this loop, we will design a circuit named MINI-PC. This circuit includes a register, which indicates at which cycle of the loop the processor is. This circuit takes has two inputs:
- clock: the clock,
- reset: to reset register of the MINI-PC to 0.
The output of the MINI-PC is named mini-pc. It gives at which cycle of loop the processor is. With an automatic clock, the mini-pc should takes the values 0, 1, 2, 3, 4, 0, 1 etc.
We will implement MINI-PC by modifying COUNTER, which already counts from 0 to 4. For that, first rename the circuit COUNTER into MINI-PC. and then modifies the inputs and output of the circuit.
Integration of MINI-PC
Add MINI-PC in CPU. You should position MINI-PC on top of CLOCK with enough space to add a HexDisplay, which shows the current value of MINI-PC.
The ENCODER circuit
We will now design our instruction set. For that, we will implement a circuit named ENCODER. This circuit will not be used in CPU, but is very useful to understand how the processor encodes the instructions.
When the processor interprets an instruction, it considers that:
- %insnl:
- bit 0 = mem: when mem = 0, the instruction uses the ALU, otherwise, it accesses memory,
- bit 1 = imm: If imm = 0, the instruction performs an operation only with registers, for example, addiu %r2, %r1, %r0. Otherwise, the instruction performs an operation with an immediate value encoded in the instruction, for example, li %r3, 442.
- bit 2 = wm: indicates if the memory access is a load or a store when mem = 1.
- if mem = 1 and wm = 0, the instruction loads from memory. In this case, it loads the value pointed by %rA into %sR,
- if mem = 1 and wm = 1, the instruction writes in memory. In this case, it writes %rD in the location pointed by %rA.
- bit 3-4 = fun: when mem = 0, gives the function executed by ALU,
- bit 5-7 = sR: gives the selector of the result register (i.e. the register modified by the instruction).
- %insnh:
- If imm = 0, then the 8 bits of %insnh are used to store the immediate operand of the instruction. For example, for li %r3, 442, %insnh = 442. In this case, sA = sR and D takes the value of %insnh.
- Otherwise:
- bits 0-2 = sA: selector for the first operand,
- bits 3-5 = sD: selector for the second operand.
Implement a DECODER circuit that takes as input mem, imm, wm, fun, sR, sA, sD and val, and that outputs the value %insnl and %insnh. By using the DECODER circuit, how the two following codes are encoded?
- Internal loop of the processor:
lb %insnl, (%pc) # load the byte pointed by %pc in %insnl addiu %pc, 1 # %pc <- %pc + 1 lb %insh, (%pc) # load the byte pointed by %pc in %insnh addiu %pc, 1 # %pc <- %pc + 1
-
Program executed by the user:
li %r1, $0x80 # load the immediate value 0x80 in %r1 lb %r0, (%r1) # load the byte pointed by %r1 in %r0 addiu %r0, $1 # %r0 <- %r0 + 1 sb %r0, (%r1) # store %r0 in the byte pointed by %r1 addiu %pc, $0xf8 # %pc <- %pc - 8 (jmp to the first load byte)
The MICROCODE circuit
We will now design the MICROCODE circuit, which implements the main loop of the processor. This circuit takes as input insnl-in/insnh-in and the mini-pc. It outputs the instruction that have to be executed according to the mini-pc, which we name insnl-out/insnh-out. In details, if:
- mini-pc = 0, it outputs a1 07,
- mini-pc = 1, it outputs e2 01,
- mini-pc = 2, it outputs c1 07,
- mini-pc = 3, it outputs e2 01,
- mini-pc = 4, it outputs insnl-in insnh-in
In order to ease the implementation, we will use two ROMs to store the microcode a1 07 e2 01 c1 07 e2 01. A ROM is a read-only memory. We can easily implement a ROM with registers, but, to simplify, we will use the ROM provided by circuitverse. The ROM is the 9th element of the "Sequential Elements" menu of the "Circuit Elements" panel. A ROM takes as input an address A (left connector) and a flag En (Enable, bottom connector), which has to be equal to 1 to activate the ROM. It outputs the value at the address A in D (right connector).
The first ROM gives the low part of the current instruction (a1 e2 c1 e2) and the second ROM gives the high part (07 01 07 01). To change the content of a cell in the ROM, you just have to double click on the cell.
When mini-pc = 0, 1, 2 or 3, we use mini-pc as the address in the two ROMs, and the circuit outputs the content of the ROMs. When mini-pc = 4, the circuit outputs insnl-in and insnh-in.
Implement the MICROCODE circuit.
Integration of the MICROCODE circuit
Add the MICROCODE circuit in the CPU circuit and connect it adequately. Add HexDisplays to see the values of insnl-out and insnh-out. Integrating MICROCODE between CLOCK and REGS is a good idea:
- At the left, MICROCODE takes mini-pc as input,
- At the bottom right, it takes the insnl/insnh output of REGS as input,
- At the up right, it outputs insnl-out/insnh-out.
By playing with wr, sR, R, you can set values in %insnl and %insnh. Verify that insnl-out and insnh-out are correct: they contain the microcode when mini-pc = 0, 1, 2 or 3, and %insnl/%insnh when mini-pc = 4.
Memory
We will now add a memory in our processor. In details, we will add a ROM, which will contain an application, and a RAM, which is writable and will be used to store the values used by the program.
Start by adding a RAM at the right of REGS. The 10th element of the "Sequential Elements" of the "Circuit Elements" is a RAM. You can connect the reset input of the CPU to the reset connector of the RAM (middle bottom). Add an 1-bit input wm connected to the W input of the RAM. We will use wm to write in memory. Finally, connect the A of REGS to the A of RAM, and the D of REGS to the DI (data in) of RAM.
Now, we will add the ROM on top of the RAM. Write this content in the ROM: 22 80 01 01 02 01 05 01 e2 f8 (see the ENCODER question). Add a 1-bit constant equal to 1, and connect it to the En entry of the ROM. Then, with a 8-bit splitter, splits A into 4 1 1 1 1. The first four bits are used as the ROM address: you can directly connect them to the A entry of the ROM. With the other 4 bits, you can now if you have to access the RAM or the RAM: when one of the other 4 bits is equal to 1, it means that the instruction accesses the RAM, otherwise, it accesses the ROM. By using a OR gate with 4 inputs, you can thus now if you have to use the output of the ROM or the output of the RAM. On the left of the RAM and ROM, you can thus use a multiplexer controlled by the result of the OR gate to select the output of the RAM or the output of the ROM. Add a HexDisplay after the multiplexer to see the result.
You can test your CPU as follow:
- First, we will test the ROM. You have to use wr/sR/R to write 6 (00000110) in pc (sR = 7). Then, while wm = 0, use sA to see the content of memory at the address 6. For that, you have to put 7 (pc) in sA. You should see that the new HexDisplay prints the value 05 since we have the value 05 at the address 6 in ROM.
- Second, we will test the RAM. You have to use wr/sR/R to write 0x10 (00010000) in %r0 (sR = 0). We will use %r1 as the address. Then, you have to use wr/sR/R to write 0xf0 (11110000) in %r1 (sR = 1). We will write %r1 at the address %r0. For that, you have to put 0 in sA and 1 in sD. If you activate wm (wm = 1), you should see that now, the new HexDisplay displays f0. If it's the case, congratulation, your memory behaves correctly!
Integration of the ALU
First, add a 8-bit input named val on top of the R input used to control the REGS circuit. Then, add the ALU circuit on top of val. You can directly connect the D output of REGS to the D input of ALU. You have to create a new 2-bit input fun and to connect it to the fun input of ALU. Add also a 1-bit input named imm. When imm = 0, you have to use the A output of REGS as the A input of ALU. When imm = 1, you have to use val as the A input of ALU. For that, you can use a multiplexer.
Now, your CPU should be correct. Add HexDisplays to see the output of the ALU (R connector). We will test the ALU as follow:
- By using wr/sR/R, writes 2 (R = 2) in %r0 (sR = 0). Then writes 6 (R = 6) in %r1 (sR = 1). If fun = 0 and imm = 0, you should see that ALU outputs the value 8.
- Write 0x0f (00001111) in val. If fun = 0 and imm = 1, you should see that ALU outputs the value 15. If it's the case, congratulation! Your processor is almost terminated.
The DECODER circuit
Currently, we manually control the ALU and the memory by using wr, sR, R, sA, sD, val, fun, imm and wm. We will design a circuit named DECODER that will generates these values by decoding the current instruction. DECODER takes as input an instruction, i.e., two 8-bit values named insnl/insnh. It outputs mem, imm, fun, sR, sA, sD, val, wm and wr:
- mem gives the bit 0 of insnl,
- imm gives the bit 1 of insnl,
- fun gives the bits 3-4 of insnl,
- sR gives the bits 5-7 of insnl,
- sA gives the bits 0-2 of insnh,
- sD = sR if imm = 1, otherwise, sD gives the bits 3-5 of insnh,
- val is a copy of insnh,
- wm = 1 if mem = 1 and the bit 2 of insnl is equal to 1. wm = 0 otherwise.
- wr = not(wm): all the instructions modify a register, except the store instruction, which writes memory without modifying a register.
Implement the DECODER circuit.
Integration of DECODER
You now just have to first remove the inputs wr, wm, mem, imm, fun, sR, sA, sD and val from CPU. Then, you have to add a DECODER circuit on top of the REGS circuit, and to connect it adequately.
You should see that your processor increments %r0 since we execute a code that load 0x80 into %r0, increments %r0 and write %r0 at 0x80.