Configuration¶
from notebook.services.config import ConfigManager
cm = ConfigManager()
cm.update('livereveal', {
'width': 1280,
'height': 720,
'theme': 'serif', # sobre et lisible
'transition': 'fade', # plus doux en cours
'controls': True,
'progress': True,
'slideNumber': True,
'history': True,
'hash': True,
'scroll': True # conserve le scroll pour les cellules longues
})
import plotly.express as px
import torch
import random
import plotly.graph_objects as go
from ipywidgets import interact, interactive, fixed, interact_manual
import math
from IPython.display import display, HTML
display(HTML("<style>.container { width:90% !important; }</style>"))
import os, random, numpy as np
SEED = 42
os.environ["PYTHONHASHSEED"] = str(SEED)
random.seed(SEED); np.random.seed(SEED)
torch.manual_seed(SEED)
torch.use_deterministic_algorithms(True)
Régularisation & optimisation¶
La dernière fois...¶
Notions¶
- Notre premier modèle de deep learning : le perceptron multi-couche
- Permet de calculer une sortie pour une entrée donnée
- Évaluation d'un modèle avec une fonction de coût
- Permet de dire si la sortie du modèle est loin de la réalité suivant une métrique
- Une méthodologie pour optimiser la fonction de coût : la descente de gradient (stochastique)
- Un algorithme pour calculer les gradients : la back propagation
Ce que nous allons voir aujourd’hui¶
Objectif. Comprendre comment faire généraliser un réseau et accélérer / fiabiliser son entraînement.
- Cadre d’évaluation : train / val / test, pièges (temporel, contextuel)
- Diagnostiquer sur-apprentissage vs sous-apprentissage
- Métriques : matrice de confusion, précision, rappel, F1, ROC-AUC, évaluation humaine
Ce que nous allons voir aujourd’hui¶
- Régularisation : pénalités L2/L1, early stopping, (intuition du dropout), data augmentation
- Optimisation : paysage de la loss, SGD, Momentum, Adagrad, RMSProp, Adam, learning rate & batch
- En pratique : checklist & petites démos
NB : fonctions d’activation et initialisation des poids seront traitées dans un autre cours.
Schéma¶
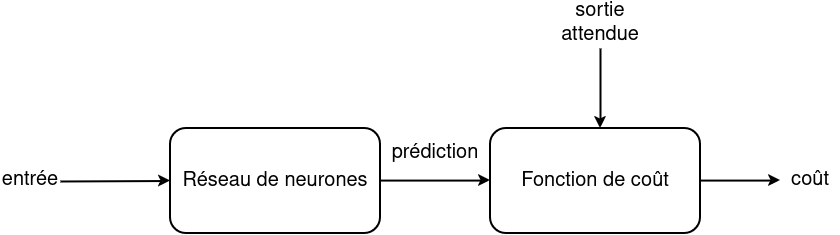
Est-ce que la fonction de coût est une garantie de qualité ?¶
- La fonction de coût n'est pas nécessairement corrélée à 100% à notre objectif business
- On va rarement nous demander de réduire la RMSE ou l'entropie croisée de nos clients
- Cependant, la vraie fonction objectif n'est pas souvent utilisable en pratique : trop longue à calculer, demande l'annotation d'humaine, pas différentiable, pas de définition mathématique claire...
- Une valeur faible sur un jeu de données en veut pas forcément dire qu'elle sera faible sur un autre jeu de données
- On aimerais que notre réseau de neurone se généralise
- Il va falloir utiliser un jeu d'entraînement, de validation et de test
Ce que nous voulons réellement mesurer, c’est la performance hors échantillon (dev/test), pas seulement la baisse du loss sur le train.
Procédure d'entraînement et d'évaluation classique¶
Algorithme
- Partage de notre dataset en sous ensembles d'entraînement (train), de validation (val) et de test (test)
- Tant que !(condition d’arrêt) — ex. early stopping sur la perte val (patience = 5), ou nombre d’epochs max
- Entraîner le réseau sur le train (en général 1 epoch, ou X itérations)
- Évaluation sur le val (coût + autres métriques automatiques)
- Évaluation sur le train (coût + autres métriques automatiques)
- Évaluation sur le test (coût + autres métriques automatiques + humains)
Train/Val/Test¶
- Généralement, on partage (split) aléatoirement notre dataset en trois sous-groupes train/val/test contenant 80%/10%/10% des données
- Peut varier suivant la taille des données, on veut que l'évaluation soit suffisamment rapide tout en étant précise
- On peut descendre à <1% pour le dev et test pour les très gros jeux de données
- Si l'on compare plusieurs baselines, bien utiliser les mêmes train/val/test
- Bien s'assurer qu'il n'y ait pas de données communes entre les sous-groupes (valeur dupliquée par exemple)
- Dans certains cas, le split ne doit pas être aléatoire
- Données temporelles : split par ordre chronologique
- val/test sur une nouveauté retrouvée en pratique : nouvelle personne, nouvel arrière-plan, ...
- Essayer d'avoir un dev et un test similaires
Découpage temporel¶
Idée clé : la chronologie prime, on évalue sur du futur, pas sur du “mélangé”.
# Données complètes
X = torch.arange(-5, 5, 0.05)
Y = X + 3 * torch.sin(5 * X)
fig = px.scatter(
x=X, y=Y,
title="Données complètes (régression jouet)",
labels={"x": "x", "y": "y"}
)
fig.update_traces(marker_size=5, opacity=0.7)
fig.update_layout(margin=dict(l=20, r=20, t=50, b=20))
fig.show()
# Split aléatoire : 80% train / 20% test = Trop Facile
X = torch.arange(-5, 5, 0.05)
Y = X + 3 * torch.sin(5 * X)
perm = torch.randperm(len(X))
split = int(0.8 * len(X))
train_idx, test_idx = perm[:split], perm[split:]
fig = go.Figure(data=[
go.Scatter(x=X[train_idx], y=Y[train_idx], mode="markers", name="train"),
go.Scatter(x=X[test_idx], y=Y[test_idx], mode="markers", name="test"),
])
fig.update_layout(
title="Split aléatoire naïf = trop facile",
xaxis_title="x", yaxis_title="y",
legend_title_text="Jeu"
)
fig.show()
# Un découpage temporel permet de mieux valider la généralisabilité
X = torch.arange(-5, 5, 0.05)
Y = X + 3 * torch.sin(5 * X)
cut = int(0.8 * len(X))
train_idx = torch.arange(0, cut)
test_idx = torch.arange(cut, len(X))
fig = go.Figure(data=[
go.Scatter(x=X[train_idx], y=Y[train_idx], mode="markers", name="train"),
go.Scatter(x=X[test_idx], y=Y[test_idx], mode="markers", name="test"),
])
fig.add_vline(x=float(X[cut]), line_dash="dash", annotation_text="frontière temporelle", annotation_position="top")
fig.update_layout(
title="Découpage temporel (mieux pour valider la généralisation)",
xaxis_title="x", yaxis_title="y", legend_title_text="Jeu"
)
fig.show()
Découpage contextuel¶
- Compétition "The Nature Conservancy Fisheries Monitoring" : identifier automatiquement des poissons.
- Très bons scores en validation interne, forte chute sur le test final.
- Raison : le test final contient de nouveaux bateaux → les modèles avaient appris l’arrière-plan (bateau ↔ type de poisson), pas le poisson.

Découpage contextuel¶
- Compétition "State Farm Distracted Driver Detection" : classifier des conducteurs distraits.
- Chute sur test final car le test introduit de nouvelles personnes.
- Le split de validation doit éviter que la même personne soit à la fois en train et en val/test.

- Outils pratiques : GroupKFold / GroupShuffleSplit (scikit-learn) quand plusieurs échantillons partagent un groupe (utilisateur, appareil, bateau…).
Évaluation¶
- Le loss (train/val) donne une approximation du progrès d'entraînement, pas la performance métier.
- On choisit des métriques alignées avec l'objectif :
- Classification : Accuracy (⚠️ classes déséquilibrées), Précision, Rappel, F1, ROC-AUC, PR-AUC.
- Régression : MAE, RMSE, $R^2$, médiane des erreurs (robuste aux outliers).
- Cas ambigus / objectifs qualitatifs : prévoir une évaluation humaine (jury, guidelines, double-annotation).
Règle d'or : ne touche jamais au test final pendant le dev. Le seuil (0.5→autre) se choisit sur validation.
Matrice de confusion¶
On compte dans une matrice le nombre d'occurrences des couples (prédiction, valeur vraie).
Convention utilisée ici : colonnes = vérité, lignes = prédiction.

Matrice de confusion - Exemple¶

Métrique : Accuracy¶
L'accuracy correspond au taux de prédictions correctes
$$accuracy = \frac{TP + TN}{TP + TN + FP + FN}$$
⚠️ Déséquilibre : si 99% de négatifs, prédire “négatif” tout le temps donne 99% d'accuracy mais 0 rappel sur la classe positive.
→ Toujours regarder Précision/Rappel/F1 (et PR-AUC) quand les classes sont déséquilibrées.
Métrique : Précision¶
La précision est la part de prédictions positives qui sont correctes.
$$\text{precision} = \frac{TP}{TP + FP}$$
À privilégier quand les faux positifs coûtent cher (ex. déclencher une action onéreuse, alerter un client, investir). Exemples :
- Détection d'opportunité trading : on préfère peu d'alertes mais fiables.
- Système d’alerte “intervention technicien” : mieux vaut être sûr avant d’envoyer quelqu’un.
Seuil ≠ 0.5 : on peut exiger une précision cible (ex. 95%) en relevant le seuil, au prix d’un rappel plus faible.
Remarque : On peut se permettre de dire "je ne sais pas" en faisant une prédiction négative et répondre à peu de prédictions positivement pour avoir un très bon score.
Métrique : Rappel¶
Le rappel mesure le taux d'élements positifs prédits comme tels par le modèle
$$rappel = \frac{TP}{TP + FN}$$
Cette métrique se concentre sur le fait de détecter toutes les occurrences positives, quitte à faire des erreurs sur les négatives.
Quand le rappel est prioritaire :
- Détection d'anomalies critiques (sécurité industrielle)
- Dépistage médical (mieux vaut ne pas rater un positif)
Remarque : Pour avoir un score parfait, il suffit de tout prédire en positif.
Métrique : F1¶
Le score F1 est un compromis entre la précision et le rappel
$$F1 = \frac{precision \times rappel}{precision + rappel}$$
Il permet d'éviter les cas très faciles pour la précision et le rappel.
$F_\beta$ généralise : $\beta>1$ favorise le rappel, $\beta<1$ la précision.
Multiclasse :
- macro : moyenne simple des classes (équilibre l'attention)
- weighted : pondérée par le support (utile si classes déséquilibrées)
- micro : agrège TP/FP/FN globaux (pertinent si tailles de classes très différentes)
Métrique : Courbe ROC¶
La courbe ROC consiste à tracer le taux de vrai positif en fonction du taux de faux positifs (parfois, on trace aussi la précision en fonction du rappel, la courbe PR).
Pour en extraire une métrique, on prend l'aire sous la courbe (AUC = Area Under the Curve) : plus elle est grande, meilleur est le modèle.
Remarque : Comment faire varier TP et FP ? On peut jouer sur la valeur de seuil, usuellement à 0.5.
ROC vs PR : si la classe positive est rare, préférez aussi la courbe PR et la PR-AUC (plus sensible à la qualité des positifs).
fig = px.area(x=[0, 1], y=[0, 1])
fig.update_layout(xaxis_title='FPR', yaxis_title='TPR', title="ROC — Classificateur aléatoire (AUC = 0.5)")
fig.show()
En-dessous de l’aléatoire → souvent étiquettes inversées, fuite de données, ou score au signe inversé.
Inverser peut “sauver” la perf, mais vérifier d’abord les données.
fig = px.area(x=[0, 1], y=[1, 1])
fig.update_layout(xaxis_title='FPR', yaxis_title='TPR', title="Classificateur parfait")
fig.show()
fig = px.area(x=[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
y=[0.1, 0.32, 0.40, 0.45, 0.7, 0.81, 0.89, 0.93, 0.94, 0.98, 1.0])
fig.update_layout(xaxis_title='FPR', yaxis_title='TPR', title="Cas général")
fig.show()
Évaluation humaine¶
Pour être sur de notre évaluation, la manière la plus simple et efficace est de demander à des humains d'annoter les résultats.
Il y a des nombreuses manières de faire l'annotation, par exemple une annotation binaire (vrai/faux) ou multi-critère (dire pourquoi c'est faux).
Même dans ce cas, il se peut que les humains ne soient pas d'accord sur l'annotation. On demande alors à plusieurs humains d'annoter la même prédiction et on utilise un score d'accord (ex: le kappa de Cohen).
Mini-protocole d’évaluation humaine
- Échantillon : tirer aléatoirement N exemples par classe (stratifié)
- Consignes : critères clairs + exemples limites (3–5 min)
- Double annotation (2 annotateurs) → calculer accord (Cohen’s κ)
- Arbitrage : un 3ᵉ annotateur tranche les désaccords
- Rapport : inclure % erreurs acceptables (tolérance métier)
⚠️ Sélectionnez les exemples à l’aveugle (pas “les pires” cas), et geler le protocole avant de regarder les résultats.
Particulièrement utile dans les sciences sociales
Choix des hyperparamètres¶
Les hyperparamètres sont des paramètres de notre système qui ne sont pas appris mais décidés par un humain.
Exemples : learning rate, nombre de couches et de neurones, ...
On les trouve en essayant plusieurs combinaisons et en comparant les performances sur le jeu de validation (et pas de test !).
On peut réutiliser les techniques vues en machine learning : random search, grid search
Surapprentissage¶
Le surapprentissage (ou overfitting) est un phénomène qui se traduit par de bonnes performances sur le jeu d'entraînement, mais par des performances dégradées sur des valeurs non vues (par exemple, le jeu de validation ou de test).
Remarque : Si l'on fait beaucoup d'expériences pour trouver des hyperparamètres, il est possible de finir par overfit sur le jeu de validation !
# Régression 1D : overfit (relier les points)
X = torch.arange(-2, 2, 0.1)
Y_true = X**2
# "train" échantillonné + bruit
idx = torch.arange(0, len(X), 3)
X_train = X[idx]
Y_train = Y_true[idx] + (torch.rand(len(idx)) - 0.5) / 2
fig = go.Figure([
go.Scatter(x=X_train, y=Y_train, mode="markers", name="train (bruité)"),
# "overfit" = relier exactement les points de train
go.Scatter(x=X_train, y=Y_train, mode="lines", name="surajusté (relie les points)")
])
fig.update_layout(
title="Régression — Courbe qui colle au bruit = overfit",
xaxis_title="x", yaxis_title="y", legend_title_text=""
)
fig.show()
X = torch.arange(-2, 2, 0.1)
Y_true = X**2
idx = torch.arange(0, len(X), 3)
X_train = X[idx]
Y_train = Y_true[idx] + (torch.rand(len(idx)) - 0.5) / 2
fig = go.Figure([
go.Scatter(x=X_train, y=Y_train, mode="markers", name="train (bruité)"),
go.Scatter(x=X, y=Y_true, mode="lines", name="modèle lisse (≈ vraie fonction)")
])
fig.update_layout(
title="Régression — Modèle plus généralisable (ne colle pas au bruit)",
xaxis_title="x", yaxis_title="y", legend_title_text=""
)
fig.show()
X = torch.arange(-1, 1, 0.01)
Y = torch.sigmoid(100*X)
X_test = [-0.9, -0.8, -0.75, -0.7, -0.68, -0.61, -0.59, -0.54, 0.53, 0.60, 0.69, 0.71, 0.74, 0.76, 0.79, 0.84]
Y_test = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1]
fig = go.Figure([
go.Scatter(x=X_test, y=Y_test, mode="markers", marker_color="red", name="dataset"),
go.Scatter(x=X, y=Y, mode="lines", line_color="blue", name="Modèle")
])
fig.add_vrect(x0="-0.5", x1="0.5",
annotation_text="Pas de données", annotation_position="top left",
fillcolor="red", opacity=0.25, line_width=0)
fig.update_layout(title="Modèle de classification trop confiant dans une zone sans donnée")
fig.add_hline(y=0.5, line_dash="dot", annotation_text="seuil 0.5", annotation_position="right")
fig.update_layout(xaxis_title="x", yaxis_title="P(y=1)")
fig.show()
X = torch.arange(-1, 1, 0.01)
Y = torch.sigmoid(10*X)
X_test = [-0.9, -0.8, -0.75, -0.7, -0.68, -0.61, -0.59, -0.54, 0.53, 0.60, 0.69, 0.71, 0.74, 0.76, 0.79, 0.84]
Y_test = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1]
fig = go.Figure([
go.Scatter(x=X_test, y=Y_test, mode="markers", marker_color="red", name="dataset"),
go.Scatter(x=X, y=Y, mode="lines", line_color="blue", name="Modèle")
])
fig.add_vrect(x0="-0.5", x1="0.5",
annotation_text="Pas de données", annotation_position="top left",
fillcolor="red", opacity=0.25, line_width=0)
fig.update_layout(title="Modèle de classification sûrement plus généralisable",
xaxis_title="x", yaxis_title="P(y=1)")
fig.add_hline(y=0.5, line_dash="dot", annotation_text="seuil 0.5", annotation_position="right")
fig.show()
La courbe bleue représente la probabilité d'appartenir à la classe 1.
Comment détecter un surapprentissage ?¶
Sur les métriques finales, comparez vos métriques entre le train et le dev.
- Si train >> dev => overfit
- Si train > dev => ok ou overfit
- Si train ~ dev => ok ou underfit ou dev trop simple
- Si dev << train => Votre dev a un problème (trop facile)
Comment détecter un surapprentissage ?¶
Sur les courbes d'apprentissage, comparez train vs validation (pour une métrique à maximiser ; pour une loss, inverser le raisonnement).
| Train ↑/↓ | Val ↑/↓ | Lecture rapide |
|---|---|---|
| ↑ | ↓ | Overfit (le modèle mémorise) |
| ↓ | ↓ | Underfit (modèle trop simple / mauvais features) |
| ↑ | ↑ | OK (ou fuite si val est trop facile) |
| ↓ | ↑ | Cas rare → vérifier données/splits |
Indices visuels : écart train–val qui se creuse, val qui remonte alors que train continue de baisser.
Sous-apprentissage / Underfit¶
Le sous-apprentissage est un phénomène qui apparaît quand les performances du modèles ne sont pas "suffisamment bonnes", c'est-à-dire que l'apprentissage n'est pas terminé ou le modèle n'est pas assez complexe ou est incorrectement paramétré.
Causes fréquentes
- Modèle trop simple / régularisation trop forte
- Pas assez d'epochs / LR trop faible
- Features insuffisantes ou cibles très bruitées
X = torch.arange(-2, 2, 0.1)
Y = X * 0 + 0.5
X_test = torch.Tensor([-1, -0.8, -0.4, 0.1, 0.2, 0.3, 0.7, 1.1])
Y_test = X_test * X_test + (torch.rand(len(X_test)) - 0.5) / 2 # On ajoute du bruit
fig = go.Figure([
go.Scatter(x=X_test, y=Y_test, mode="markers", marker_color="red", name="dataset"),
go.Scatter(x=X, y=Y, mode="lines", line_color="blue", name="Modèle")
])
fig.update_layout(
title="Sous-apprentissage — Modèle constant (trop simple)",
xaxis_title="x", yaxis_title="y", legend_title_text=""
)
fig.show()
Comment détecter un sous-apprentissage ?¶
Il faut définir ce que signifie des performances "suffisamment bonnes". Souvent, cela signifie des performances comparables à un humain.
On peut donc faire annoter des données en entrée par des humains pour qu'ils nous donnent la sortie. Ensuite, on calcule les performances des humains (souvent pas 100% pour des tâches un peu complexes).
- Si train et dev << humain => underfit
- Si train et dev ~ humain => ok
- Si train et dev >> humain => Fantastique !
Checks rapides
- Augmentez légèrement la capacité (plus de neurones / moins de régularisation) → la val monte ? (alors vous étiez sous-ajusté)
- Laissez plus d'epochs → la val monte puis redescend ?
Réduire le sur-apprentissage avec la régularisation¶
Idée clé. On contraint le modèle pour améliorer la généralisation (au prix d’un peu d’erreur train).
Ce que nous voyons maintenant :
- Régularisation L2 et L1 (intuitions, effets)
- Gradient avec L2 et lien avec weight decay
- Où l’appliquer
Qu'est-ce que la régularisation ?¶
La régularisation est un ensemble de techniques pénalisant la complexité afin réduire les erreurs de généralisation (overfit sur le dev et test) en ayant le moins d'impact possible sur l'erreur d'entraînement (sur le train).
Contraindre les poids par la fonction de coût¶
Une première méthode pour contrôler la généralisabilité consiste à imposer des contraintes sur les poids. Elles peuvent s'intégrer directement dans la fonction de coût.
$$J(W) = \frac{1}{n} \sum_{i=1}^n \mathcal{L}(f(x^{(i)}; W), y^{(i)}) + \lambda \cdot R(W)$$
où $\lambda$ est un hyperparamètre donnant plus ou moins d'importance à la régularisation et $R(W)$ est une fonction pénalisant les poids dans certaines configurations.
Fonctions de régularisation classiques¶
- L2 : $R(W)=\lVert W\rVert_2^2=\sum_{i,j} W_{i,j}^2$ — rétrécit les poids (peu de 0 exacts), lisse
- L1 : $R(W)=\lVert W\rVert_1=\sum_{i,j} \lvert W_{i,j}\rvert$ — favorise la sparsité (zéros)
- Elastic Net : $\lambda_1 \lVert W\rVert_1 + \lambda_2 \lVert W\rVert_2^2$ — compromis L1/L2
Exemples¶
Soit $x = [1,1,1,1]^T$.
$w_1 = [1, 0, 0, 0]^T$
$\lVert w_1\rVert_2^2 = 1,\ \lVert w_1\rVert_1 = 1,\ w_1^T x = 1$$w_2 = [0.25, 0.25, 0.25, 0.25]^T$
$\lVert w_2\rVert_2^2 = 4\times 0.25^2 = 0.25,\ \lVert w_2\rVert_1 = 1,\ w_2^T x = 1$$w_3 = [4, -1, -1, -1]^T$
$\lVert w_3\rVert_2^2 = 16+1+1+1 = 19,\ \lVert w_3\rVert_1 = 7,\ w_3^T x = 1$
Lecture. Même sortie ($w^T x = 1$), mais pénalités très différentes : L2 préfère $w_2$, L1 aime la sparsité de $w_1$.
Gradient de la régularisation L2¶
$$ J_{\text{reg}}(W)=J(W)+\lambda \lVert W\rVert_2^2 \quad\Rightarrow\quad \nabla J_{\text{reg}}(W)=\nabla J(W)+2\lambda W $$
Mise à jour descente de gradient : $$ W_{t+1} = W_t - \eta\big(\nabla J(W_t) + 2\lambda W_t\big) = (1 - 2\eta\lambda)\,W_t\;-\;\eta\,\nabla J(W_t) $$
Posons $\alpha = 2\eta\lambda$ : $W_{t+1}=(1-\alpha)W_t - \eta\,\nabla J(W_t)$
Weight decay¶
Le weight decay consiste à retirer un peu de $W_t$ à chaque mise à jour, ce qui est équivalent à une régularisation L2 pour des optimisateurs simples.
Remarque : Souvent, vous verrez mentionné le weight decay dans les arguments de l'optimisateur. Dans ce cas, ce n'est pas la peine de rajouter de la régularisation L2.
Optimisation avancée¶
Objectif : converger plus vite et plus sûrement.
Nous verrons :
- Momentum (inertie)
- Adagrad (normalisation adaptative)
- RMSProp (poids récents)
- Adam (Momentum + adaptatif)
Problèmes avec la descente de gradient stochastique¶
- Convergence lente quand la pente est grande suivant une direction et petite suivant une autre.
- Le gradient fait de grands aller-retours dans un cas, et de petits sauts dans l'autre
- Reste bloqué dans des minima locaux et des points selle
- Le gradient y est nul
- Mauvais conditionnement (vallées étroites) → zig-zag et convergence lente
- L'aspect stochastique crée du bruit
def show_sgd():
X = torch.arange(-2, 2, 0.1)
Y = torch.arange(-2, 2, 0.1)
Z = []
for x in X:
temp = []
for y in Y:
temp.append(10 * x * x + y * y)
Z.append(temp)
Z = torch.Tensor(Z)
X_descent, Y_descent, Z_descent = [-1.5], [-1.5], [11 * 1.5 * 1.5]
lr = 0.095
for _ in range(10):
X_descent.append(X_descent[-1] - lr * 2 * 10 * X_descent[-1])
Y_descent.append(Y_descent[-1] - lr * 2 * Y_descent[-1])
Z_descent.append(10 * X_descent[-1] * X_descent[-1] + Y_descent[-1] * Y_descent[-1])
fig = go.Figure(data=[
go.Surface(z=Z.T, x=X, y=Y)
])
fig.update_traces(
contours_z=dict(show=True, usecolormap=True, highlightcolor="limegreen", project_z=True))
fig.update_layout(
title="SGD sur surface anisotrope : zig-zag (10·w1² + w2²)",
scene=dict(
xaxis_title="w1", yaxis_title="w2", zaxis_title="J(w1,w2)",
camera=dict(eye=dict(x=1.6, y=1.6, z=0.9))
),
margin=dict(l=0, r=0, b=0, t=40)
)
fig.add_trace(
go.Scatter3d(x=X_descent, y=Y_descent, z=Z_descent, marker_color="red"))
fig.show()
fig2 = go.Figure()
fig2.add_trace(go.Contour(
x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J"))
fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD"))
fig2.update_layout(title="Projection 2D — Trajectoire de SGD", xaxis_title="w1", yaxis_title="w2")
fig2.show()
show_sgd()
import plotly.graph_objects as go
fig2 = go.Figure()
fig2.add_trace(go.Contour(
x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J"))
fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD"))
fig2.update_layout(title="Projection 2D — Trajectoire de SGD", xaxis_title="w1", yaxis_title="w2")
fig2.show()
--------------------------------------------------------------------------- NameError Traceback (most recent call last) Cell In[32], line 4 1 import plotly.graph_objects as go 2 fig2 = go.Figure() 3 fig2.add_trace(go.Contour( ----> 4 x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J")) 5 fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD")) 6 fig2.update_layout(title="Projection 2D — Trajectoire de SGD", xaxis_title="w1", yaxis_title="w2") NameError: name 'Z' is not defined
def show_local_minimum():
x = torch.arange(-2, 2, 0.01)
t = -2
t_descent = [t]
y_descent = [2.0 - 1 * t - 2 * t ** 2 + 0.16 * t ** 3 + 0.5 * t**4]
lr = 0.2
for _ in range(10):
t = t_descent[-1]
grad = -1 - 4 * t + 0.16 * 3 * t ** 2 + 2 * t ** 3
t = t - lr * grad
t_descent.append(t)
y_descent.append(2.0 - 1 * t - 2 * t ** 2 + 0.16 * t ** 3 + 0.5 * t**4)
fig = go.Figure([
go.Scatter(x=x, y=2.0 - 1 * x - 2 * x ** 2 + 0.16 * x ** 3 + 0.5 * x**4, name="fonction"),
go.Scatter(x=t_descent, y=y_descent, mode="lines+markers", marker=dict(size=10, color="red"), name="valeur")
])
fig.show()
show_local_minimum()
import torch, numpy as np
import plotly.graph_objects as go
def show_local_minimum(lr=0.05, iters=80, x0=(1.5, 1.0), seed=0, with_momentum=False, beta=0.9):
torch.manual_seed(seed)
# Paysage non convexe : "vallées" + minima locaux
def f(x, y):
# double puits + terme quadratique léger
return (x**2 + y**2) + 3*torch.sin(2*x)*torch.cos(2*y)
def grad(x, y):
df_dx = 2*x + 3*2*torch.cos(2*x)*torch.cos(2*y)
df_dy = 2*y - 3*2*torch.sin(2*x)*torch.sin(2*y)
return torch.stack([df_dx, df_dy], dim=-1)
# grille pour contours
gx = torch.linspace(-3, 3, 200)
gy = torch.linspace(-3, 3, 200)
XX, YY = torch.meshgrid(gx, gy, indexing="xy")
ZZ = f(XX, YY)
# descente
xy = torch.tensor(x0, dtype=torch.float32)
traj = [xy.clone()]
v = torch.zeros_like(xy)
for _ in range(iters):
g = grad(xy[0], xy[1]).squeeze()
print(xy, f(xy[0], xy[1]))
if with_momentum:
v = beta*v + (1-beta)*g
xy = xy - lr * v
else:
xy = xy - lr * g
traj.append(xy.clone())
traj = torch.stack(traj)
Xd, Yd = traj[:,0].numpy(), traj[:,1].numpy()
# plot
fig = go.Figure()
fig.add_trace(go.Contour(x=gx.numpy(), y=gy.numpy(), z=ZZ.numpy().T,
contours_coloring="lines", showscale=False, name="niveaux J"))
fig.add_trace(go.Scatter(x=Xd, y=Yd, mode="markers+lines", name="trajectoire"))
fig.add_trace(go.Scatter(x=[x0[0]], y=[x0[1]], mode="markers", name="départ", marker_symbol="x", marker_size=12))
fig.update_layout(
title=f"Descente {'avec momentum' if with_momentum else 'SGD'} — f(x,y)=(x²+y²)+3·sin(2x)·cos(2y)",
xaxis_title="x", yaxis_title="y", legend_title_text=""
)
fig.show()
show_local_minimum(lr=0.01)
tensor([1.5000, 1.0000]) tensor(0.5494) tensor([1.4553, 0.9777]) tensor(0.3668) tensor([1.4138, 0.9613]) tensor(0.2445) tensor([1.3749, 0.9504]) tensor(0.1707) tensor([1.3379, 0.9446]) tensor(0.1367) tensor([1.3023, 0.9435]) tensor(0.1361) tensor([1.2674, 0.9466]) tensor(0.1649) tensor([1.2328, 0.9537]) tensor(0.2204) tensor([1.1983, 0.9645]) tensor(0.3008) tensor([1.1635, 0.9786]) tensor(0.4046) tensor([1.1284, 0.9958]) tensor(0.5301) tensor([1.0930, 1.0156]) tensor(0.6748) tensor([1.0573, 1.0376]) tensor(0.8356) tensor([1.0216, 1.0614]) tensor(1.0080) tensor([0.9860, 1.0865]) tensor(1.1870) tensor([0.9510, 1.1123]) tensor(1.3671) tensor([0.9169, 1.1383]) tensor(1.5428) tensor([0.8840, 1.1640]) tensor(1.7093) tensor([0.8527, 1.1891]) tensor(1.8629) tensor([0.8231, 1.2132]) tensor(2.0012) tensor([0.7954, 1.2359]) tensor(2.1230) tensor([0.7697, 1.2573]) tensor(2.2284) tensor([0.7461, 1.2771]) tensor(2.3181) tensor([0.7245, 1.2953]) tensor(2.3935) tensor([0.7048, 1.3120]) tensor(2.4563) tensor([0.6869, 1.3272]) tensor(2.5081) tensor([0.6708, 1.3410]) tensor(2.5507) tensor([0.6562, 1.3535]) tensor(2.5854) tensor([0.6430, 1.3648]) tensor(2.6137) tensor([0.6311, 1.3750]) tensor(2.6366) tensor([0.6205, 1.3842]) tensor(2.6553) tensor([0.6109, 1.3925]) tensor(2.6704) tensor([0.6023, 1.4000]) tensor(2.6826) tensor([0.5945, 1.4067]) tensor(2.6925) tensor([0.5875, 1.4127]) tensor(2.7005) tensor([0.5813, 1.4182]) tensor(2.7070) tensor([0.5756, 1.4231]) tensor(2.7123) tensor([0.5705, 1.4276]) tensor(2.7166) tensor([0.5660, 1.4316]) tensor(2.7201) tensor([0.5619, 1.4352]) tensor(2.7229) tensor([0.5581, 1.4384]) tensor(2.7252) tensor([0.5548, 1.4414]) tensor(2.7271) tensor([0.5518, 1.4440]) tensor(2.7286) tensor([0.5491, 1.4464]) tensor(2.7299) tensor([0.5466, 1.4486]) tensor(2.7309) tensor([0.5444, 1.4506]) tensor(2.7317) tensor([0.5424, 1.4523]) tensor(2.7324) tensor([0.5406, 1.4539]) tensor(2.7329) tensor([0.5390, 1.4554]) tensor(2.7334) tensor([0.5375, 1.4567]) tensor(2.7337) tensor([0.5362, 1.4579]) tensor(2.7340) tensor([0.5350, 1.4590]) tensor(2.7343) tensor([0.5339, 1.4599]) tensor(2.7345) tensor([0.5329, 1.4608]) tensor(2.7347) tensor([0.5320, 1.4616]) tensor(2.7348) tensor([0.5312, 1.4623]) tensor(2.7349) tensor([0.5305, 1.4630]) tensor(2.7350) tensor([0.5298, 1.4636]) tensor(2.7351) tensor([0.5292, 1.4641]) tensor(2.7351) tensor([0.5287, 1.4646]) tensor(2.7352) tensor([0.5282, 1.4651]) tensor(2.7352) tensor([0.5278, 1.4655]) tensor(2.7352) tensor([0.5274, 1.4658]) tensor(2.7353) tensor([0.5270, 1.4662]) tensor(2.7353) tensor([0.5267, 1.4664]) tensor(2.7353) tensor([0.5264, 1.4667]) tensor(2.7353) tensor([0.5261, 1.4670]) tensor(2.7353) tensor([0.5259, 1.4672]) tensor(2.7354) tensor([0.5257, 1.4674]) tensor(2.7354) tensor([0.5255, 1.4676]) tensor(2.7354) tensor([0.5253, 1.4677]) tensor(2.7354) tensor([0.5251, 1.4679]) tensor(2.7354) tensor([0.5250, 1.4680]) tensor(2.7354) tensor([0.5248, 1.4681]) tensor(2.7354) tensor([0.5247, 1.4683]) tensor(2.7354) tensor([0.5246, 1.4684]) tensor(2.7354) tensor([0.5245, 1.4684]) tensor(2.7354) tensor([0.5244, 1.4685]) tensor(2.7354) tensor([0.5244, 1.4686]) tensor(2.7354) tensor([0.5243, 1.4687]) tensor(2.7354)
# Plusieurs redémarrages pour voir les minima atteints
starts = [(1.5, 1.0), (-2.0, 1.2), (0.5, -2.5), (2.2, -0.8)]
for i, s in enumerate(starts):
show_local_minimum(lr=0.05, iters=80, x0=s, seed=i)
Ajouter de l'inertie avec le Momentum¶
- Idée : On peut garder une trace des mouvements précédents en construisant une vitesse de déplacement
- Dévier de cette vitesse est compliqué
- La vitesse est la moyenne glissante des gradients
$$v_0 = 0$$ $$ v_t=\beta\,v_{t-1}+(1-\beta)\,\nabla J(W_t) $$ $$ W_{t+1}=W_t-\eta\,v_t $$ avec typiquement $\beta\in[0.9,0.95]$.
Intuition. On lisse les gradients et on accélère dans les directions stables → moins de zig-zag dans les vallées étroites.
def show_momentum():
X = torch.arange(-2, 2, 0.1)
Y = torch.arange(-2, 2, 0.1)
Z = []
for x in X:
temp = []
for y in Y:
temp.append(10 * x * x + y * y)
Z.append(temp)
Z = torch.Tensor(Z)
X_descent, Y_descent, Z_descent = [-1.5], [-1.5], [11 * 1.5 * 1.5]
lr = 0.095
beta = 0.4
v_x, v_y = 0, 0
for _ in range(20):
if v_x != 0:
v_x = beta * v_x + (1 - beta) * 2 * 10 * X_descent[-1]
v_y = beta * v_y + (1 - beta) * 2 * Y_descent[-1]
else:
v_x = 2 * 10 * X_descent[-1]
v_y = 2 * Y_descent[-1]
X_descent.append(X_descent[-1] - lr * v_x)
Y_descent.append(Y_descent[-1] - lr * v_y)
Z_descent.append(10 * X_descent[-1] * X_descent[-1] + Y_descent[-1] * Y_descent[-1])
fig = go.Figure(data=[
go.Surface(z=Z.T, x=X, y=Y)
])
fig.update_layout(
title="SGD avec moment sur surface anisotrope : zig-zag (10·w1² + w2²)",
scene=dict(
xaxis_title="w1", yaxis_title="w2", zaxis_title="J(w1,w2)",
camera=dict(eye=dict(x=1.6, y=1.6, z=0.9))
),
margin=dict(l=0, r=0, b=0, t=40)
)
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.add_trace(
go.Scatter3d(x=X_descent, y=Y_descent, z=Z_descent, marker_color="red"))
fig.show()
fig2 = go.Figure()
fig2.add_trace(go.Contour(
x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J"))
fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD"))
fig2.update_layout(title="Projection 2D — Trajectoire avec le moment", xaxis_title="w1", yaxis_title="w2")
fig2.show()
show_momentum()
def show_momentum_local_mimumum():
x = torch.arange(-2, 2, 0.01)
t = -2
t_descent = [t]
y_descent = [2.0 - 1 * t - 2 * t ** 2 + 0.16 * t ** 3 + 0.5 * t**4]
lr = 0.2
beta = 0.4
v = 0
for _ in range(10):
t = t_descent[-1]
grad = -1 - 4 * t + 0.16 * 3 * t ** 2 + 2 * t ** 3
if v != 0:
v = beta * v + (1 - beta) * grad
else:
v = grad
t = t - lr * v
t_descent.append(t)
y_descent.append(2.0 - 1 * t - 2 * t ** 2 + 0.16 * t ** 3 + 0.5 * t**4)
fig = go.Figure([
go.Scatter(x=x, y=2.0 - 1 * x - 2 * x ** 2 + 0.16 * x ** 3 + 0.5 * x**4, name="fonction"),
go.Scatter(x=t_descent, y=y_descent, mode="lines+markers", marker=dict(size=10, color="red"), name="valeur")
])
fig.show()
show_momentum_local_mimumum()
Normaliser les gradients avec Adagrad¶
Idée. Pas adaptatif par paramètre : les dimensions souvent sollicitées reçoivent des pas plus petits.
$$G_0 = 0$$ $$G_t = G_{t-1} + \nabla J_t(W)^2$$ (chaque élément est mis au carré) $$W_t = W_{t-1} - \eta * \frac{\nabla J_t(W)}{\sqrt{G_t} + \epsilon}$$
On utilise $\epsilon$ pour éviter une division par 0.
Limite. Le taux effectif décroît sans cesse → peut s’arrêter trop tôt.
(Solutions: RMSProp, Adam.)
def show_adagrad():
X = torch.arange(-2, 2, 0.1)
Y = torch.arange(-2, 2, 0.1)
Z = []
for x in X:
temp = []
for y in Y:
temp.append(10 * x * x + y * y)
Z.append(temp)
Z = torch.Tensor(Z)
X_descent, Y_descent, Z_descent = [-1.5], [-1.5], [11 * 1.5 * 1.5]
lr = 0.4
g_x = 0
g_y = 0
for _ in range(10):
grad_x = 2 * 10 * X_descent[-1]
grad_y = 2 * Y_descent[-1]
g_x = g_x + grad_x * grad_x
g_y = g_y + grad_y * grad_y
X_descent.append(X_descent[-1] - lr * grad_x / (math.sqrt(g_x) +1e-7))
Y_descent.append(Y_descent[-1] - lr * grad_y / (math.sqrt(g_y) + 1e-7))
Z_descent.append(10 * X_descent[-1] * X_descent[-1] + Y_descent[-1] * Y_descent[-1])
fig = go.Figure(data=[
go.Surface(z=Z.T, x=X, y=Y)
])
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.add_trace(
go.Scatter3d(x=X_descent, y=Y_descent, z=Z_descent, marker_color="red"))
fig.show()
fig2 = go.Figure()
fig2.add_trace(go.Contour(
x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J"))
fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD"))
fig2.update_layout(title="Projection 2D — Trajectoire de Adagrad", xaxis_title="w1", yaxis_title="w2")
fig2.show()
show_adagrad()
Normaliser en donnant plus d'importance aux points récents : RMSProp¶
Idée : Au lieu de prendre la somme des normes commes dans AdaGrad, on veut donner plus d'importance aux gradients récents.
$$G_0 = 0$$ $$G_t = \delta * G_{t-1} + (1 - \delta) * \nabla J_t(W)^2$$ $$W_t = W_{t-1} - \eta * \frac{\nabla J_t(W)}{\sqrt{G_t} + \epsilon}$$
avec $\delta\approx 0.9$.
def show_rmsprop():
X = torch.arange(-2, 2, 0.1)
Y = torch.arange(-2, 2, 0.1)
Z = []
for x in X:
temp = []
for y in Y:
temp.append(10 * x * x + y * y)
Z.append(temp)
Z = torch.Tensor(Z)
X_descent, Y_descent, Z_descent = [-1.5], [-1.5], [11 * 1.5 * 1.5]
lr = 0.4
g_x = 0
g_y = 0
delta = 0.1
for _ in range(10):
grad_x = 2 * 10 * X_descent[-1]
grad_y = 2 * Y_descent[-1]
g_x = delta * g_x + (1 - delta) * grad_x * grad_x
g_y = delta * g_y + (1 - delta) * grad_y * grad_y
X_descent.append(X_descent[-1] - lr * grad_x / (math.sqrt(g_x) +1e-7))
Y_descent.append(Y_descent[-1] - lr * grad_y / (math.sqrt(g_y) + 1e-7))
Z_descent.append(10 * X_descent[-1] * X_descent[-1] + Y_descent[-1] * Y_descent[-1])
fig = go.Figure(data=[
go.Surface(z=Z.T, x=X, y=Y)
])
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.add_trace(
go.Scatter3d(x=X_descent, y=Y_descent, z=Z_descent, marker_color="red"))
fig.show()
fig2 = go.Figure()
fig2.add_trace(go.Contour(
x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J"))
fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD"))
fig2.update_layout(title="Projection 2D — Trajectoire de RMSProp", xaxis_title="w1", yaxis_title="w2")
fig2.show()
show_rmsprop()
Combiner l'inertie avec la normalisation : Adam¶
Idée : On veut à la fois le comportement du momentum et de RMSProp
$$moment^1_0 = 0$$ $$moment^2_0 = 0$$ $$moment^1_t = \beta_1 * moment^1_{t-1} + (1 - \beta_1) * \nabla J_t(W)$$ (momentum) $$moment^1_t = \beta_2 * moment^2_{t-1} + (1 - \beta_2) * \nabla J_t(W)^2$$ (RMSProp) $$moment\_debiaisé^1_t = \frac{moment^1_t}{1 - \beta_1^t}$$ $$moment\_debiaisé^2_t = \frac{moment^2_t}{1 - \beta_2^t}$$ $$W_t = W_{t-1} - \eta \frac{moment\_debiaisé^1}{\sqrt{moment\_debiaisé^2} + \epsilon}$$
def show_adam():
X = torch.arange(-2, 2, 0.1)
Y = torch.arange(-2, 2, 0.1)
Z = []
for x in X:
temp = []
for y in Y:
temp.append(10 * x * x + y * y)
Z.append(temp)
Z = torch.Tensor(Z)
X_descent, Y_descent, Z_descent = [-1.5], [-1.5], [11 * 1.5 * 1.5]
lr = 0.1
m1_x, m1_y, m2_x, m2_y = 0, 0, 0, 0
beta1, beta2 = 0.9, 0.999
for t in range(1, 21):
grad_x = 2 * 10 * X_descent[-1]
grad_y = 2 * Y_descent[-1]
m1_x = beta1 * m1_x + (1-beta1) * grad_x
m1_y = beta1 * m1_y + (1-beta1) * grad_y
m2_x = beta2 * m2_x + (1-beta2) * grad_x * grad_x
m2_y = beta2 * m2_y + (1-beta2) * grad_y * grad_y
m1_x_unbais = m1_x / (1 - beta1 ** t)
m1_y_unbais = m1_y / (1 - beta1 ** t)
m2_x_unbais = m2_x / (1 - beta2 ** t)
m2_y_unbais = m2_y / (1 - beta2 ** t)
X_descent.append(X_descent[-1] - lr * m1_x_unbais / (math.sqrt(m2_x_unbais) +1e-7))
Y_descent.append(Y_descent[-1] - lr * m1_y_unbais / (math.sqrt(m2_y_unbais) + 1e-7))
Z_descent.append(10 * X_descent[-1] * X_descent[-1] + Y_descent[-1] * Y_descent[-1])
fig = go.Figure(data=[
go.Surface(z=Z.T, x=X, y=Y)
])
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.add_trace(
go.Scatter3d(x=X_descent, y=Y_descent, z=Z_descent, marker_color="red"))
fig.show()
fig2 = go.Figure()
fig2.add_trace(go.Contour(
x=X, y=Y, z=Z.T.numpy(), contours_coloring="lines", showscale=False, name="niveaux J"))
fig2.add_trace(go.Scatter(x=X_descent, y=Y_descent, mode="markers+lines", name="trajectoire SGD"))
fig2.update_layout(title="Projection 2D — Trajectoire de Adam", xaxis_title="w1", yaxis_title="w2")
fig2.show()
show_adam()
En pratique¶
Par défaut, on va utiliser AdamW (=Adam + weight decay) avec comme paramètres $\beta_1 = 0.9$, $\beta_2 = 0.999$, un taux d'apprentissage variant entre $1*10^{-3}$ et $1*10^{-4}$ (1e-3, 5e-4, et 1e-4 par exemple), et un weight decay entre $1*10^{-2}$ et $1*10^{-4}$.
Adam(W) (et SGD, Adagrad, RMSProp) sont implémentés dans Pytorch !
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from torch import nn
import torch.nn.functional as f
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
iris = load_iris()
x = iris.data
y = iris.target
# Découpage du dataset
# Sklearn ne permet pas de couper en trois directement
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.25)
# On crée des tenseurs
x_train=torch.FloatTensor(x_train)
x_val=torch.FloatTensor(x_val)
x_test=torch.FloatTensor(x_test)
y_train=torch.LongTensor(y_train)
y_val=torch.LongTensor(y_val)
y_test=torch.LongTensor(y_test)
class LinearModel(nn.Module):
def __init__(self, in_dim=4, hidden_dim=10, out_dim=3):
super().__init__()
self.linear1 = nn.Linear(in_dim, hidden_dim)
self.linear2 = nn.Linear(hidden_dim, out_dim)
def forward(self, x):
out1 = f.relu(self.linear1(x))
return self.linear2(out1)
losses_train = []
losses_val = []
accuracies = []
model = LinearModel()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters())
# Boucle d'entraînement
for epoch in range(5000):
# Ici, on ne fait pas de batch
optimizer.zero_grad() # On met les gradients à 0
outputs = model(x_train)
loss = criterion(outputs, y_train)
loss.backward()
optimizer.step() # Fait tout pour nous
# Validation
with torch.no_grad():
val_outputs = model(x_val)
loss_val = criterion(val_outputs, y_val)
losses_val.append(loss_val.item())
# On prend l'indice avec la plus haute valeur
_, predicted = torch.max(val_outputs, 1)
accuracy = accuracy_score(y_val, predicted)
accuracies.append(accuracy)
losses_train.append(loss.item())
# Test
with torch.no_grad():
test_outputs = model(x_test)
_, predicted = torch.max(test_outputs, 1)
# precision / recall / f1 score
precision = precision_score(y_test, predicted, average='weighted')
recall = recall_score(y_test, predicted, average='weighted')
f1 = f1_score(y_test, predicted, average='weighted')
print(f'Test Accuracy: {accuracy * 100:.2f}%')
Test Accuracy: 100.00%
fig = go.Figure([
go.Scatter(x=list(range(len(losses_train))), y=losses_train, name="train"),
go.Scatter(x=list(range(len(losses_val))), y=losses_val, name="val"),
])
fig.show()
fig = go.Figure([
go.Scatter(x=list(range(len(accuracies))), y=accuracies, name="Val accuracy"),
])
fig.show()
En résumé¶
- Procédure d'entraînement
- Overfit, underfit
- Découpage du dataset et cas particuliers
- Métriques de classification
- Régularisation et weight decay
- Le moment
- Optimiseur : Adam(W), AdaGrad, RMSProp
Ressources additionnelles¶
- http://web.archive.org/web/20240314024529/https://introtodeeplearning.com/slides/6S191_MIT_DeepLearning_L1.pdf
- https://m2dsupsdlclass.github.io/lectures-labs/slides/02_backprop/index.html#64
- https://www.deeplearningbook.org/contents/regularization.html
- https://web.eecs.umich.edu/~justincj/slides/eecs498/WI2022/598_WI2022_lecture04.pdf
- https://dataflowr.github.io/website/modules/4-optimization-for-deep-learning/