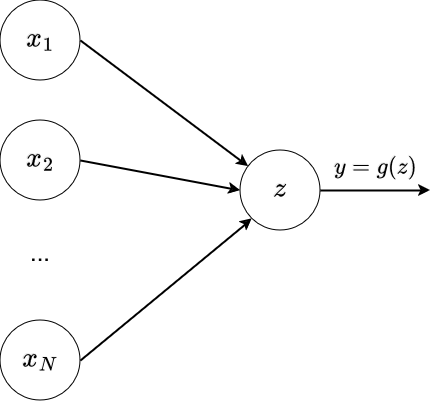
Configuration¶
from notebook.services.config import ConfigManager
cm = ConfigManager()
cm = ConfigManager()
cm.update('livereveal', {
'width': 1280,
'height': 720,
'theme': 'serif', # sobre et lisible
'transition': 'fade', # plus doux en cours
'controls': True,
'progress': True,
'slideNumber': True,
'history': True,
'hash': True,
'scroll': True # conserve le scroll pour les cellules longues
})
import torch
import plotly.express as px
import plotly.graph_objects as go
import torch.nn as nn
import torch.nn.functional as F
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
import plotly.figure_factory as ff
import graphviz
def gv(s):
return graphviz.Source('digraph G{ rankdir="LR"; ' + s + ' }')
from IPython.display import display, HTML
display(HTML("<style>.container { width:90% !important; }</style>"))
import os, random, numpy as np
SEED = 42
os.environ["PYTHONHASHSEED"] = str(SEED)
random.seed(SEED); np.random.seed(SEED)
torch.manual_seed(SEED)
torch.use_deterministic_algorithms(True)
Objectifs du cours¶
- Comprendre les réseaux de neurones, les fonctions d’activation et les fonctions de perte.
- Expliquer la forward pass d’un perceptron sur un exemple chifré.
- Savoir appliquer la descente de gradient (batch/mini-batch/SGD).
- Visualiser la backpropagation sur un petit graphe de calcul.
Prérequis : régression linéaire/logistique, dérivation élémentaire, Python/NumPy.
À la fin : vous entraînez un classifieur simple et interprétez ses courbes.
Qu’est-ce qu’un réseau de neurones ?¶
Rappels de machine learning¶
Rappel : Régression linéaire¶
Nous avons une entrée $X = (x_1, ..., x_N) \in \mathbb{R}^N$ et une sortie $y \in \mathbb{R}$. Quand nous faisons une régression linéaire, nous cherchons à approcher la sortie du mieux possible à l'aide d'une combinaison linéaire. Soit $W = (w_1, ..., w_N) \in \mathbb{R}^{1 \times N}$ les coefficients de la régression linéaire et $b\in\mathbb{R}$ le biais, la sortie de la régression linéaire $\hat{y}$ est donnée par :
$$\hat{y} = w_1 * x_1 + ... + w_N * x_N + b = \sum_{i=1}^{N} w_i * x_i$$
- On met souvent un chapeau sur la sortie du réseau pour la différencier de la sortie attendue.
import torch
X = torch.tensor([1., 2., 3., 4.]) # (4,)
W = torch.tensor([[0.1, -0.5, 0.3, 0.4]]) # (1,4)
b = torch.tensor([0.2]) # (1,)
print(f"X shape={tuple(X.shape)}, W shape={tuple(W.shape)}, b shape={tuple(b.shape)}")
z = W @ X + b
print("z =", z.item())
X shape=(4,), W shape=(1, 4), b shape=(1,) z = 1.8000000715255737
- La bibliothèque torch a beaucoup de fonctionnalités similaires à Numpy (Torch ≈ Numpy + autograd + GPU).
- L'opérateur @ permet de faire une multiplication de matrices.
- Par défaut, Tensor est un tenseur de flottant sur 32 bits. On peut contrôler le type avec torch.LongTensor, IntTensor, DoubleTensor, ... doc
Rappel : Régression logistique¶
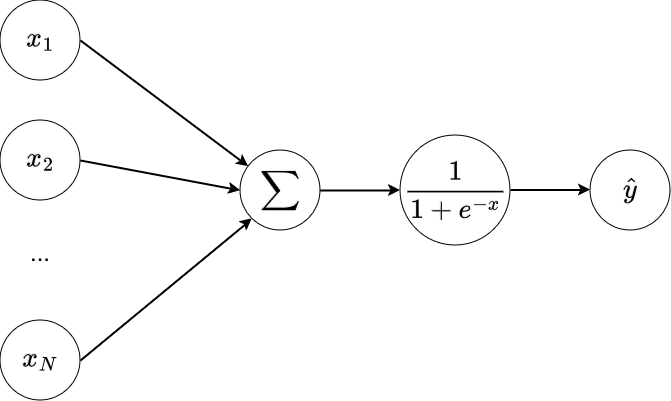
Quand nous voulons résoudre un problème de classification binaire, il faut transformer la sortie en un nombre entre 0 et 1 que l'on interprète comme une probabilité. La transformation se fait à l'aide de la fonction logistique (fonction sigmoid dans notre cas):
$$\hat{y} = \frac{1}{1+e^{-(\sum_{i=1}^{N} x_i * w_i) + b}}=\sigma(WX + b)$$ $$X\in\mathbb{R}^{N},\; W\in\mathbb{R}^{N},\; b\in\mathbb{R},\; \hat y\in(0,1)$$
X = torch.tensor([1., 2., 3., 4.]) # (4,)
W = torch.tensor([[0.1, -0.5, 0.3, 0.4]]) # (1,4)
b = torch.tensor([0.2]) # (1,)
z = W @ X + b # (1,)
y = torch.sigmoid(z)
print(f"X{tuple(X.shape)}, W{tuple(W.shape)}, b{tuple(b.shape)} -> z={z.item():.3f}, σ(z)={y.item():.3f}")
X(4,), W(1, 4), b(1,) -> z=1.800, σ(z)=0.858
X = torch.linspace(-10, 10, 400)
Y = torch.sigmoid(X)
dY = Y*(1-Y)
fig = go.Figure()
fig.add_scatter(x=X.numpy(), y=Y.numpy(), name="σ(z)")
fig.add_scatter(x=X.numpy(), y=dY.numpy(), name="σ'(z)")
fig.add_scatter(x=[0], y=[0.5], mode="markers", name="z=0 → 0.5")
fig.update_layout(title="Sigmoïde & dérivée", xaxis_title="z", yaxis_title="valeur")
fig
Représentation graphique¶
Nous pouvons représenter notre formule visuellement en montrant la chaîne des calculs.
Le Perceptron¶
Le perceptron et la forward propagation¶
Nous pouvons généraliser notre régression logistique en remplaçant la sigmoid par une fonction non-linéaire "quelconque". Nous obtenons le perceptron.
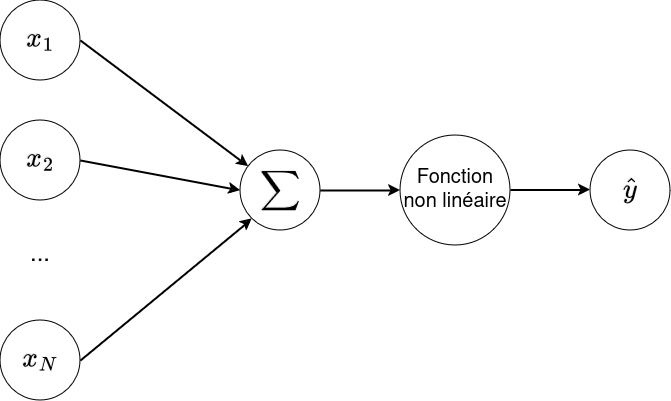
$$\hat{y} = g(\sum_{i=1}^N w_i * x_i + b) = g(WX + b) $$
où $g$ est une fonction non linéaire appelée fonction d'activation
Forme matricielle¶
En utilisant la forme matricielle, nous pouvons appliquer le perceptron à plusieurs entrées en une seule opération. Quand on manipule plusieurs entrée simultanément, on parle de batch.
$$\underbrace{\hat Y}_{1\times m} = \underbrace{g}_{\text{élément par élément}}\!\Big(\;\underbrace{WX}_{1\times m} + \underbrace{b}_{1\times 1}\mathbf{1}^\top\Big)$$
où $X\in\mathbb{R}^{N\times m}$ (m exemples colonnes), $W\in\mathbb{R}^{1\times N}$, $b\in\mathbb{R}^{1\times1}$, $\mathbf{1}\in \mathbb{R}^{M\times1}$ (vecteur ne contenant que des 1).
En pratique, utiliser un produit scalaire (ou une multiplication de matrice) est beaucoup plus rapide que de faire une boucle pour la somme.
Pourquoi g doit-elle être non linéaire ?¶
Imaginons que $g$ soit une fonction linéaire avec comme coefficients $V = (v_1, ..., v_N) \in \mathbb{R}^N$. On aurait :
$$\hat{y} = \sum_{i=1}^N w_i * v_i * x_i = \sum_{i=1}^N u_i * x_i$$
Avec $u_i = w_i * v_i$. On retombe sur une régression linéaire !
Cependant, nous voulons exploiter des phénomènes complexes, rarement linéaire. Il nous faut donc plus d'expressivité.
import torch, plotly.express as px
X = torch.tensor([[0.,0.],[0.,1.],[1.,0.],[1.,1.]])
y = torch.tensor([0.,1.,1.,0.])
fig = px.scatter(x=X[:,0].numpy(), y=X[:,1].numpy(), color=y.numpy().astype(str),
labels={'x':'x1','y':'x2'}, title="XOR : non linéairement séparable")
fig
N'oublions pas le biais...¶
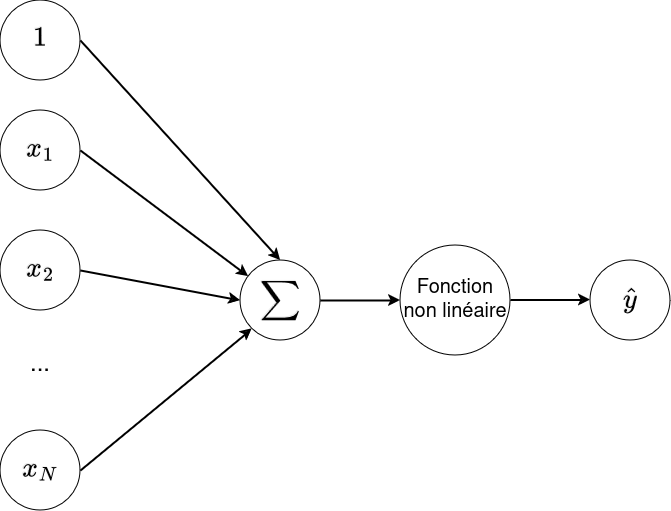
On peut l'intégrer directement dans l'entrée $\hat{y} = g(w_0 + \sum_{i=1}^N w_i * x_i)$
Fonctions d'activation usuelles¶
Fonctions d'activation usuelles - Sigmoid¶
La fonction sigmoid :
$$\sigma(x) = \frac{1}{1+e^{-x}}$$
avec pour dérivée :
$$ \sigma'(x) = \sigma(x)(1-\sigma(x))$$
- Nous verrons plus loin pourquoi la dérivée est important
- Comment choisir la bonne fonction ? Il faut essayer et voir les propriétés de chacunes (voir plus tard).
X = torch.linspace(-10, 10, 400)
Y = torch.sigmoid(X)
dY = Y*(1-Y)
fig = go.Figure()
fig.add_scatter(x=X.numpy(), y=Y.numpy(), name="σ(z)")
fig.add_scatter(x=X.numpy(), y=dY.numpy(), name="σ'(z)")
fig.add_scatter(x=[0], y=[0.5], mode="markers", name="z=0 → 0.5")
fig.update_layout(title="Sigmoïde & dérivée", xaxis_title="z", yaxis_title="valeur")
fig
Fonctions d'activation usuelles - Tangente hyperbolique¶
La fonction tangente hyperbolique :
$$g(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$
avec pour dérivée :
$$g'(x) = 1 - g(x)^2$$
X = torch.arange(-10, 10, 0.1)
Y = torch.tanh(X)
dev_Y = 1.0 - Y * Y
fig = go.Figure([go.Scatter(x=X, y=Y, name="tanh"), go.Scatter(x=X, y=dev_Y, name="Dérivée")])
fig.show()
Fonctions d'activation usuelles - Rectified Linear Unit¶
La fonction Rectified Linear Unit (ReLU) :
$$g(x) = max(0, x)$$
avec pour dérivée :
$$g'(x) = \left\{ \begin{array}{ll} 1 & x > 0 \\ 0 & \mbox{sinon} \end{array} \right.$$
(Non dérivable en 0)
X = torch.linspace(-5, 5, 1000)
Y = torch.relu(X)
dY = torch.where(X>0, torch.ones_like(X), torch.zeros_like(X))
fig = go.Figure([go.Scatter(x=X, y=Y, name="ReLU"), go.Scatter(x=X, y=dY, name="Dérivée")])
fig.show()
Perceptron : Exemple¶
Perceptron : Exemple¶
- Prenons, $X = \begin{bmatrix} 1 \text{ (biais)}\\ 4.7 \\ -1.1 \end{bmatrix}$, $W = \begin{bmatrix} 4.1 \\ 0.4 \\ 2.2 \end{bmatrix}$
$$ \hat{y} = g(4.1 + 0.4 x_1 + 2.2 x_2)$$
Si nous utilisons une sigmoid, 0.5 en sortie (et donc 0 en entrée) sera la limite de décision entre la classe 0 et la classe 1 (cas d'une classification). La fonction linéaire définie une droite (ou hyperplan) :
$$ 4.1 + 0.4 x_1 + 2.2 x_2 = 0$$ $$ x_2 = \frac{-0.4}{2.2}*x_1 - \frac{4.1}{2.2} = -0.18 * x_1 - 1.86$$
X = torch.arange(-10, 10, 0.1, )
Y = -1.86 - 0.18 * X
fig = go.Figure(
[go.Scatter(x=list(X) + [min(X)], y=list(Y) + [min(Y)], fill="toself", text=["" for _ in range(len(X))] + ["Negative"], mode="markers+text", textposition="top right", name="Négative"),
go.Scatter(x=list(X) + [max(X)], y=list(Y) + [max(Y)], fill="toself", text=["" for _ in range(len(X))] + ["Positive"], mode="markers+text", textposition="bottom left", name="Positive")])
fig.show()
On sépare la zone des prédiction positives (>0) des predictions négatives (<0) avec une droite.
X = torch.arange(-10, 10, 0.1, )
Y = -1.86 - 0.18 * X
fig = go.Figure(
[go.Scatter(x=list(X) + [min(X)], y=list(Y) + [min(Y)], fill="toself", text=["" for _ in range(len(X))] + ["Negative"],mode="markers+text", textposition="top right", name="Négative"),
go.Scatter(x=list(X) + [max(X)], y=list(Y) + [max(Y)], fill="toself", text=["" for _ in range(len(X))] + ["Positive"],mode="markers+text", textposition="bottom left", name="Positive"),
go.Scatter(x=[4.7], y=[-1.1], text=["X"], mode="markers+text", textposition="top center",marker=dict(size=10), name="X")])
fig.show()
Perceptron : Exemple¶
- Prenons, $X = \begin{bmatrix} 1 \text{ (biais)}\\ 4.7 \\ -1.1 \end{bmatrix}$ et $W = \begin{bmatrix} 4.1 \\ 0.4 \\ 2.2 \end{bmatrix}$
$$ \begin{aligned} \hat{y} &= g(4.1 + 0.4 x_1 + 2.2 x_2) \\ &= sigmoid(4.1 + 0.4 * 4.7 + 2.2 * (-1.1))\\ &= sigmoid(3.56) = 0.9723 \end{aligned}$$
torch.sigmoid(torch.Tensor([1, 4.7, -1.1]) @ torch.Tensor([4.1, 0.4, 2.2]))
tensor(0.9723)
Du perceptron au réseau de neurones¶
Nous pouvons généraliser à plusieurs sorties¶
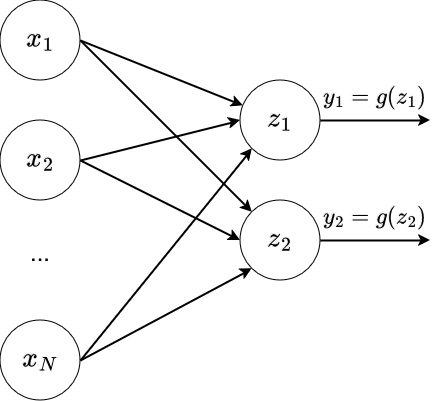
Avec $z_j = w_{0, j} + \sum_{i=1}^Nw_{i,j}x_{i}$ (chaque sortie a ses propres poids)
On se débarasse de la somme...¶
La somme est trop longue à réaliser en pratique. Ici, nous pouvons la remplacer par une multiplication de matrices :
$$Z = XW^T$$
où $X \in \mathbb{R}^{m, N}$ ($m$ batchs), $W \in \mathbb{R}^{M \times N}$, et $Z \in \mathbb{R}^{m, M}$, avec $N$ la dimension de l'entrée et $M$ la dimension de la sortie.
(ici, pour suivre les notations de torch, on met la dimension du batch en premier)
X = torch.tensor([1.0, 4.7, -1.1]) # (d,)
W = torch.tensor([[-1.2, 1.4, 1.1],
[ 0.3, 0.5, -0.9]]) # (M,d)
b = torch.tensor([0.2, -0.3]) # (M,)
z = X @ W.T + b # -> (M,)
y = torch.sigmoid(z) # ou softmax pour M>1 multi-classe
print("X", tuple(X.shape), "| W", tuple(W.shape), "| b", tuple(b.shape))
print("z", z.tolist(), "| y", y.tolist())
X (3,) | W (2, 3) | b (2,) z [4.369998931884766, 3.3399999141693115] | y [0.9875068664550781, 0.9657757878303528]
# Avec un module Pytorch
class Perceptron(nn.Module):
def __init__(self, input_size, output_size):
super().__init__()
self.W = torch.rand((output_size, input_size))
self.b = torch.rand((output_size))
def forward(self, x):
return F.sigmoid(x @ W.T + self.b)
perceptron = Perceptron(3, 2)
X = torch.Tensor([1.4, 4.7, -1.1])
print(perceptron(X))
tensor([0.9810, 0.9896])
# Pytorch fournit une fonction pour la partie linéaire
class Perceptron2(nn.Module):
def __init__(self, input_size, output_size):
super().__init__()
self.linear = nn.Linear(input_size, output_size)
def forward(self, x):
return torch.sigmoid(self.linear(x))
perceptron = Perceptron2(3, 2)
X = torch.Tensor([1.4, 4.7, -1.1])
print(perceptron(X))
tensor([0.1748, 0.8796], grad_fn=<SigmoidBackward0>)
Un autre avantage de la notation en matrice¶
On peut donner plusieurs points X en entrée, et les sorties seront calculées en parallèle.
X = torch.Tensor([[1.4, 4.7, -1.1],
[2.1, 1.8, 3.1]]) # (m=2, d=3)
print(perceptron(X)) # (2,2)
tensor([[0.1748, 0.8796],
[0.8948, 0.7605]], grad_fn=<SigmoidBackward0>)
Réseau de neurones à une couche¶
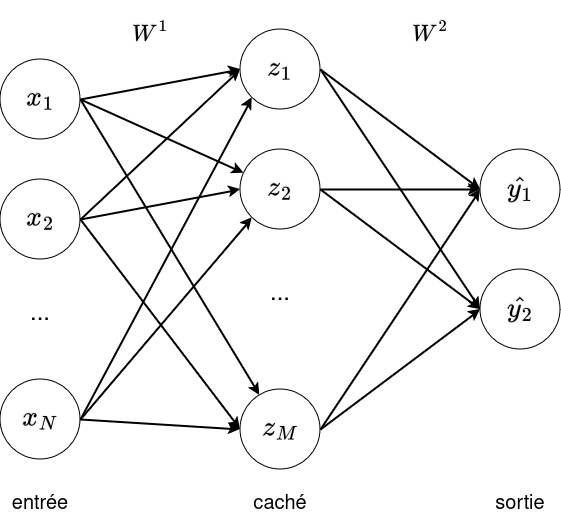
On a toujours $$z_j = w^1_{0, j} + \sum_{i=1}^Nw_{i, j}^1x_i$$ mais aussi $$\hat{y}_j = g_2(w_{0, j}^2 + \sum_{i=1}^Mw_{i, j}^2g_1(z_j))$$ ( On a $W^1 \in \mathbb{R}^{M \times N}$ et $W^2 \in \mathbb{R}^{2 \times M}$)
On peut aussi écrire l'équation avec des matrices¶
$\hat{Y} = g_2(g_1(X*W_1^T)*W_2^T)$
ou
$$ H = g_1(X W_1^\top),\quad $$ $$ Z = H W_2^\top,\quad $$ $$ \hat{Y} = g_2(Z) $$
typiquement $g_1=ReLU/Tanh$, $g2=\sigma$.
class MultiPerceptron(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
self.linear1 = nn.Linear(input_size, hidden_size)
self.linear2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
hidden = F.sigmoid(self.linear1(x))
return F.sigmoid(self.linear2(hidden))
perceptron = MultiPerceptron(3, 6, 2)
X = torch.Tensor([1, 4.7, -1.1])
print(perceptron(X))
tensor([0.4793, 0.6134], grad_fn=<SigmoidBackward0>)
Non linéarité et couche de sortie¶
Doit-on appliquer une fonction d'activation sur la dernière couche ?
En général, non.
Soit on fait de la régression et on ne peut pas supposer de l'intervalle de retour.
Soit on fait de la classification, et les autres fonctions de PyTorch transforment implicitement la sortie en une distribution de probabilité.
Comment calculer cette distribution nous-même quand nous avons plusieurs sortie (donc plusieurs classes) ?
On appelle logits le vector non normalisé qu'un modèle de classification génère.
La fonction softmax¶
Si on a un vecteur $y = [y_1, y_2, ..., y_n]$, alors la fonction softmax est définie par :
$$softmax(y)_i = \frac{e^{y_i}}{\sum_j e^{y_j}}$$
Cette fonction fait en sorte que la sortie soit une probabilité : chaque sortie est comprise entre 0 et 1, et la somme de toutes les sorties vaut 1.
logits = torch.tensor([[1.2, -0.3, 0.7]])
probas = F.softmax(logits, dim=-1)
pred = torch.argmax(logits, dim=-1)
print("probas:", probas.tolist(), "| préd:", pred.item())
probas: [[0.546549379825592, 0.12195165455341339, 0.331498920917511]] | préd: 0
Théorème d'approximation universel¶
En gros (terms and conditions apply) : N'importe quelle fonction continue peut être approximée de manière arbitrairement proche par un réseau de neurones d'une seule couche cachée avec une fonction d'activation non polynomiale et un nombre fini de neurones.
Fin du cours¶
Ce n'est pas si simple...¶
- C'est un théorème d'existence : on ne sait pas combien de neurones sont nécessaires et quels sont les poids. En particulier, même avec assez de neurones, il n'est pas garanti qu'une méthode puisse trouver les poids (c.f. descente de gradient plus tard).
- Il n'y a pas de limite sur le nombre de neurones. Peut-être faut-il 10 neurones ? 1 million ? 1 milliard ? $10^{80}$ (nombre d'atomes dans l'univers) ?
- En pratique, nous n'avons qu'un accès très limité à la fonction que l'on vise. On ne peut voir que quelques valeurs de cette fonction, et il peut y avoir du bruit.
- Comment gérer le bruit ?
- Comment faire en sorte que le modèle se généralise aux données non vues ?
La suite du cours¶
Dans la suite du cours nous nous concentrerons sur :
- Des méthodes pour trouver de bons poids (pas forcément optimaux)
- Des architectures (manière d'organiser des réseaux de neurones) donnant de bon résultats, même avec un nombre de neurones limités.
Réseau de neurones profond¶
On peut rajouter autant de couches que l'on veut. On parle de perceptron multicouche (multilayer perceptron/MLP, fully connected layer).
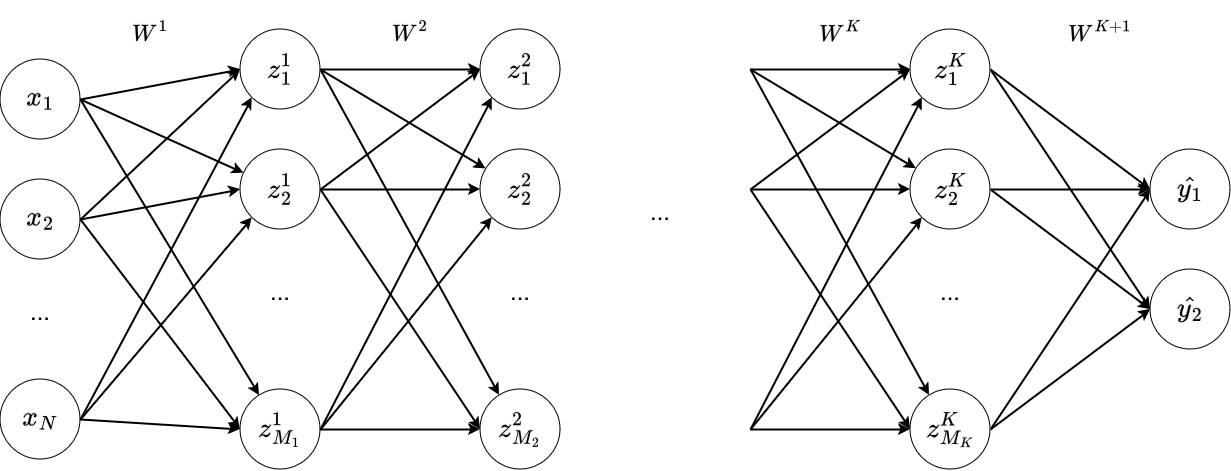
Avec $W^1 \in \mathbb{R}^{M_1 \times N}$, $W^2 \in \mathbb{R}^{M_2 \times M_1}$, ..., $W^K \in \mathbb{R}^{M_{K} \times M_{K-1}}$, $W^{K+1} \in \mathbb{R}^{2 \times M_K}$
Bien faire attention que les dimensions soient compatibles.
Exemple¶
Exemple¶
Étant donné le nombre de présences d'un étudiant et le nombre d'heures passées sur le projet du cours, prédire la probabilité de valider le cours.
Nous avons le jeu de données suivant :
positif_x = torch.Tensor([1, 2, 4, 4, 5, 6, 7])
positif_y = torch.Tensor([6.5, 4.6, 6.1, 2, 5.5, 1.9, 3.2])
negatif_x = torch.Tensor([0, 0, 1, 4])
negatif_y = torch.Tensor([0, 1.5, 0.5, 5])
test_x = torch.Tensor([3])
test_y = torch.Tensor([5.1])
fig = go.Figure([
go.Scatter(x=positif_x, y=positif_y, mode="markers", name="Positive", marker=dict(size=10, color="green")),
go.Scatter(x=negatif_x, y=negatif_y, mode="markers", name="Négative", marker=dict(size=10, color="red")),
go.Scatter(x=test_x, y=test_y, mode="markers+text", text=["?"], textposition="top center",
name="?", marker=dict(size=10, color="blue"))])
fig.show()
# Essayons de faire une prédiction avec un MLP...
torch.manual_seed(3) # Pour la reproducibilité
perceptron = MultiPerceptron(2, 4, 1)
perceptron(torch.Tensor([3, 5.1]))
tensor([0.4053], grad_fn=<SigmoidBackward0>)
Notre perceptron prédit un résultat négatif ?¶
Pourquoi ?
Les poids sont aléatoires : le réseau n'a pas encore été entrainé.
@interact(w1=(-10.0, 10.0, 0.1), w2=(-10.0, 10.0, 0.1), b=(-10.0, 10.0, 0.1))
def simple_classifier(w1=1.0, w2=1.0, b=0.0):
# Prédiction point test
logit = b + w1*test_x[0] + w2*test_y[0]
prob = torch.sigmoid(logit).item()
print(f"logit={logit.item():.3f} σ(logit)={prob:.3f} → classe={'1' if prob>=0.5 else '0'}")
# Droite z=0
r = torch.arange(0, 7, 0.05)
if abs(w2) < 1e-8: # évite division par 0
w2 = 1e-8
boundary = -(w1/w2)*r - (b/w2)
fig = go.Figure([
go.Scatter(x=positif_x, y=positif_y, mode="markers", name="Positif", marker=dict(size=10)),
go.Scatter(x=negatif_x, y=negatif_y, mode="markers", name="Négatif", marker=dict(size=10)),
go.Scatter(x=test_x, y=test_y, mode="markers+text", text=["?"], textposition="top center", name="Test", marker=dict(size=10)),
go.Scatter(x=r, y=boundary, name="Frontière (z=0)")
])
fig.update_layout(xaxis_title="x1", yaxis_title="x2", title="σ(z)=0.5 ⇔ z=0")
fig.show()
interactive(children=(FloatSlider(value=1.0, description='w1', max=10.0, min=-10.0), FloatSlider(value=1.0, de…
Fonction de coût¶
Quantifier l'erreur¶
Pour quantifier les erreurs de notre réseau, il nous faut une fonction appelée fonction de coût (loss function). Cette fonction prend en entrée une prédiction faite par notre réseau et la vraie valeur à prédire, puis retourne un score évaluant notre prédiction (plus bas = meilleur).
$$\mathcal{L}(\underbrace{f(x^{(i)}; W)}_{\text{prédiction}}, \underbrace{y^{(i)}}_{\text{vraie valeur}})$$
Ici, $\mathcal{L}$ est notre fonction de coût, $f$ est notre réseau de neurones qui a pour poids $W$, $x^{(i)}$ est un exemple d'entrée et $y^{(i)}$ est la sortie correcte associée.
Le coût empirique¶
Le coût empirique de notre réseau est le total ou la moyenne des coûts sur notre jeu de données.
$$J(W) = \frac{1}{n} \sum_{i=1}^n \mathcal{L}(f(x^{(i)}; W), y^{(i)})$$
Nous n'avons aucun autre moyen d'estimer les performances du réseau sans données.
Exemples de fonctions de coût¶
Entropie croisée binaire¶
Le coût d'entropie croisée binaire (binary cross entropy) est une fonction de coût utilisée pour évaluer un classifieur binaire qui sort une probabilité entre 0 et 1.
$$\mathcal{L}(f(x^{(i)}; W), y^{(i)}) = -(y^{(i)} log(f(x^{(i)}; W)) + (1 - y^{(i)}) log(1 - f(x^{(i)}; W))$$
Ajout : Quelques mots sur l'entropie ? Interprétation ?
L'erreur quadratique¶
L'erreur quadratique moyenne (mean squared error) est une fonction de coût utilisée pour évaluer un modèle sortant des nombres réels quelconques (régression).
$$\mathcal{L}(f(x^{(i)}; W), y^{(i)}) = (f(x^{(i)}; W) - y^{(i)})^2$$
Choisir une fonction de coût¶
Il existe beaucoup de fonction de coût différentes. Les plus génériques sont implémentées dans les bibliothèques directement (ici pour Torch). En général:
- Binaire (1 logit) →
BCEWithLogitsLoss - Multi-classe exclusive (C logits) →
CrossEntropyLoss(softmax implicite) - Multi-label (C logits indépendants) →
BCEWithLogitsLoss
Cependant, il arrive souvent que l'on personnalise cette fonction de coût pour se rapprocher au mieux d'une métrique propre à notre application.
@interact(w1=(-10.0,10.0,0.1), w2=(-10.0,10.0,0.1), b=(-10.0,10.0,0.1))
def simple_regression(w1=0.0, w2=1.0, b=0.0):
# Données concaténées
X = torch.stack([torch.cat([positif_x, negatif_x]),
torch.cat([positif_y, negatif_y])], dim=1) # (n,2)
y = torch.cat([torch.ones(len(positif_x)), torch.zeros(len(negatif_x))])# (n,)
z = b + w1*X[:,0] + w2*X[:,1] # logits
loss = F.binary_cross_entropy_with_logits(z, y)
print(f"Loss moyenne (BCE logits) = {loss.item():.4f}")
# Prédiction point test
zt = b + w1*test_x[0] + w2*test_y[0]
pt = torch.sigmoid(zt).item()
print(f"logit={zt.item():.3f} σ={pt:.3f} → classe={'1' if pt>=0.5 else '0'}")
# Frontière z=0
r = torch.arange(0,7,0.05)
eps = 1e-8 if abs(w2)<1e-8 else 0.0
boundary = -(w1/(w2+eps))*r - (b/(w2+eps))
fig = go.Figure([
go.Scatter(x=positif_x, y=positif_y, mode="markers", name="Positif"),
go.Scatter(x=negatif_x, y=negatif_y, mode="markers", name="Négatif"),
go.Scatter(x=test_x, y=test_y, mode="markers+text", text=["?"], name="Test"),
go.Scatter(x=r, y=boundary, name="Frontière (z=0)")
])
fig.update_layout(xaxis_title="x1", yaxis_title="x2", title="BCE & frontière σ(z)=0.5 ⇔ z=0")
fig.show()
interactive(children=(FloatSlider(value=0.0, description='w1', max=10.0, min=-10.0), FloatSlider(value=1.0, de…
Ici, on s'amuse à minimiser le coût en fonction des paramètres du système.
La descente de gradient¶
On veut optimiser la fonction de coût automatiquement...¶
Nous voulons trouver les poids du réseau qui nous donnent un coût minimal
$$W^* = argmin_W \frac{1}{n} \sum_{i=1}^{n} \mathcal{L}(f(x^{(i)}; W), y^{(i)})$$
Ici $W$ contient tous les paramètres de notre réseau de neurones (tous les poids de toutes les couches), $W^*$ est le poids optimal.
def display_3D():
# Nous fixons b pour pouvoir visualiser la fonction de coût en fonction des poids
b = -8.5
x, y, z = torch.arange(1, 3, 0.01), torch.arange(0, 2, 0.01), []
for w_1 in x:
temp = []
for w_2 in y:
all_pos = torch.sigmoid(b + w_1 * positif_x + w_2 * positif_y)
all_neg = torch.sigmoid(b + w_1 * negatif_x + w_2 * negatif_y)
temp.append((sum(-torch.log(all_pos)) + sum(-torch.log(1 - all_neg))) / (len(all_pos) + len(all_neg)))
z.append(temp)
z = torch.Tensor(z) #.clamp(max=0.10) # Je mets un max pour voir le minimum
fig = go.Figure(data=[go.Surface(z=z.T, x=x, y=y)])
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.show()
display_3D()
Nous affichons la fonction de coût en fonction de deux paramètres avec notre petit dataset. On voit à peu près où se situe le minimum (dans les intervalles considérés).
def display_3D():
perceptron = MultiPerceptron(2, 10, 1)
x, y, z = torch.arange(-10, 10, 0.05), torch.arange(-10, 10, 0.05), []
X = torch.Tensor([list(positif_x) + list(negatif_x), list(positif_y) + list(negatif_y)]).T
Y = torch.Tensor([1 for _ in range(len(positif_x))] + [0 for _ in range(len(negatif_x))]).reshape(-1, 1)
for w_1 in x:
temp = []
perceptron.linear1.weight.data[0, 0] = w_1.item()
for w_2 in y:
perceptron.linear1.weight.data[0, 1] = w_2.item()
y_pred = perceptron(X)
loss = F.binary_cross_entropy(y_pred, Y)
temp.append(loss)
z.append(temp)
z = torch.Tensor(z)
fig = go.Figure(data=[go.Surface(z=z.T, x=x, y=y)])
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.show()
torch.manual_seed(42)
display_3D()
Avec un perceptron multi-couche, ma fonction de coût est maintenant plus complexe.
Tracé impossible en pratique¶
- Il y a trop de points à calculer
- On ne sait pas où se concentrer
- On ne connait pas la précision recherchée
- Fonction de coût très compliquée et non convexe
Peut-on automatiser la recherche des poids optimaux ?
Si je considère un point donné, comment l'améliorer ?¶
Solution : je regarde autour et je me déplace dans la direction qui semble la plus favorable
@interact(t=(-2.0, 2.0, 0.1))
def search_minimum(t=1.4):
x = torch.arange(-2, 2, 0.1)
fig = go.Figure([
go.Scatter(x=x, y=x**2),
go.Scatter(x=[t], y=[t*t], mode="markers", marker=dict(size=10, color="red"))
])
fig.show()
interactive(children=(FloatSlider(value=1.4, description='t', max=2.0, min=-2.0), Output()), _dom_classes=('wi…
Rechercher à la main.
Comment connaitre la "bonne direction" ?¶
Localement, on peut utiliser la dérivée. La dérivée "pointe" vers l'augmentation de la fonction. Quand la dérivée est positive, la fonction croit (localement, si x augmente, y augmente), et quand la dérivée est négative, la fonction décroit. Il suffit donc de diminuer x quand la dérivée est positive, sinon de l'augmenter.
Fonctionne uniquement localement, impossible de trouver la direction parfaite en pratique.
@interact(t=(-2.0, 2.0, 0.1))
def search_minimum(t=1.4):
x = torch.arange(-2, 2, 0.1)
print("La dérivée vaut :", 2 * t)
fig = go.Figure([
go.Scatter(x=x, y=x**2, name="fonction"), go.Scatter(x=x, y=2*x, name="dérivée"),
go.Scatter(x=[t], y=[t*t], mode="markers", marker=dict(size=10, color="red"), name="valeur")
])
fig.show()
interactive(children=(FloatSlider(value=1.4, description='t', max=2.0, min=-2.0), Output()), _dom_classes=('wi…
@interact(t=(-2.0, 2.0, 0.01))
def search_minimum(t=-1.8):
x = torch.arange(-2, 2, 0.01)
print("La dérivée vaut :", -1 - 4 * t + 0.16 * 3 * t ** 2 + 2 * t ** 3)
fig = go.Figure([
go.Scatter(x=x, y=2.0 - 1 * x - 2 * x ** 2 + 0.16 * x ** 3 + 0.5 * x**4, name="fonction"),
go.Scatter(x=x, y=-1 - 4 * x + 0.16 * 3 * x ** 2 + 2 * x ** 3, name="dérivée"),
go.Scatter(x=[t], y=[2.0 - 1 * t - 2 * t ** 2 + 0.16 * t ** 3 + 0.5 * t**4], mode="markers", marker=dict(size=10, color="red"), name="valeur")
])
fig.show()
interactive(children=(FloatSlider(value=-1.8, description='t', max=2.0, min=-2.0, step=0.01), Output()), _dom_…
La dérivée nous indique vers où nous diriger, mais on peut arriver à un minimum local.
Minimum local vs minimum global¶
Soit $f: \mathbb{R}^N \rightarrow \mathbb{R}$ une fonction et $x \in \mathbb{R}^N$. $x$ est un minimum global s'il n'existe aucun x' tel que $f(x') < f(x)$.
Un minimum global est le point le plus bas de la fonction.
$x$ est un minimum local s'il existe un $\epsilon > 0$ tel que $\forall x', \mid\mid x - x' \mid\mid < \epsilon$ on a $f(x') > f(x)$.
Un minimum local est tel que tous les points suffisamment proches ont une valeur plus élevée dans $f$.
Le minimum global est difficile voire impossible à trouver en pratique. On se contente souvent de minima locaux.
En dimension n¶
Dans le cas général, la dérivée s'appelle le gradient et chacune de ses composantes est la dérivée par rapport à une dimension de l'entrée.
$$\frac{\partial J(W)}{\partial W} = \nabla f = \begin{bmatrix} \frac{\partial J(W)}{\partial w_1} \\ \frac{\partial J(W)}{\partial w_2} \\ ... \\ \frac{\partial J(W)}{\partial w_n} \end{bmatrix}$$
Gradient - Exemple¶
$$f(X) = x_1 * x_2$$
$$\frac{\partial f(X)}{\partial X} = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \end{bmatrix}$$ Avec :
$$\frac{\partial f}{\partial x_1} = x_2$$ $$\frac{\partial f}{\partial x_2} = x_1$$
(Quand on dérive par rapport à une variable, on fait comme si toutes les autres étaient constantes)
def visualisation_gradient():
b = -8.5 # Nous fixons b pour pouvoir visualiser
x, y, z = [], [], []
for w_1 in torch.arange(1, 3, 0.1):
temp_x, temp_y, temp_z = [], [], []
for w_2 in torch.arange(0, 2, 0.1):
all_pos = torch.sigmoid(b + w_1 * positif_x + w_2 * positif_y)
all_neg = torch.sigmoid(b + w_1 * negatif_x + w_2 * negatif_y)
temp_x.append(w_1)
temp_y.append(w_2)
temp_z.append((sum(-torch.log(all_pos)) + sum(-torch.log(1 - all_neg))).item() / (len(all_pos) + len(all_neg)))
x.append(temp_x)
y.append(temp_y)
z.append(temp_z)
x = torch.Tensor(x)
y = torch.Tensor(y)
z = -torch.Tensor(z) / 10 # .clamp(max=0.1) # Pour enlever les grandes flèches
v, u = torch.gradient(z)
fig = ff.create_quiver(x, y, u, v, scale=10, arrow_scale=1, line_width=1)
#fig.add_trace(go.Scatter(x=x.reshape(-1), y=y.reshape(-1), text=["%.3f" % x for x in z.reshape(-1)], mode="markers", textposition="top center"))
fig.show()
visualisation_gradient()
De combien dois-je me déplacer ?¶
En général, on multiplie le gradient par un coefficient appelé le taux d'apprentissage (learning rate) et on soustrait le résultat au point actuel.
Ici, il y a un compromis à trouver entre :
- Un learning rate trop petit qui va rendre la convergence très longue
- Un learning rate trop grand qui va diverger
Convergence et divergence¶
- Convergence : Au fur et à mesure de l'entrainement, la fonction de coût se rapproche d'une valeur unique et se stabilise proche de cette valeur (en pratique, on fixe un seuil de convergence en dessous duquel on arrête les calculs ou on met un nombre d'itérations maximal)
- Divergence : Au fur et à mesure de l'entrainement, la fonction de coût ne se stabilise autour d'aucune valeur. Pis, elle peut même diverger vers l'infini.
Pour vérifier la convergence et la divergence, il faudra bien suivre l'évolution de la fonction de coût.
@interact(lr=(0.01, 1.3, 0.01))
def search_minimum(lr=0.01):
t = 1.5
all_t, all_t2 = [t], [t*t]
for i in range(10):
t = t - lr * 2 * t # Mise à jour
all_t.append(t)
all_t2.append(t*t)
x = torch.arange(min(-2, min(all_t)), max(2, max(all_t)), 0.01)
fig = go.Figure([
go.Scatter(x=x, y=x**2, name="fonction"),
go.Scatter(x=all_t, y=all_t2, mode="lines+markers+text", text=list(range(len(all_t))), marker=dict(size=5, color="red"), name="valeur")
])
fig.show()
interactive(children=(FloatSlider(value=0.01, description='lr', max=1.3, min=0.01, step=0.01), Output()), _dom…
Noter que pour un lr trop petit, on n'atteint pas le minimum, et pour un trop grand, on diverge.
La descente de gradient¶
Algorithme
- Initialiser les points $W$ de manière aléatoire (souvent une gaussienne centrée sur 0)
- Jusqu'à la convergence ou nombre d'itérations maximal:
- Calcul du gradient $\frac{\partial J(W)}{\partial W}$
- Mise à jour des poids $W \leftarrow W - \eta\frac{\partial J(W)}{\partial W}$ ($\eta$ = learning rate)
- Retourner les poids
Un passage dans la boucle est appelé une époque (epoch) et le nombre d'itérations maximal le nombre d'époques (number of epochs).
def descente_gradient():
perceptron = Perceptron2(2, 1)
lr = 0.05
X = torch.Tensor([list(positif_x) + list(negatif_x), list(positif_y) + list(negatif_y)]).T
Y = torch.Tensor([1 for _ in range(len(positif_x))] + [0 for _ in range(len(negatif_x))]).reshape(-1, 1)
all_losses = []
for _ in range(5000):
y_pred = perceptron(X)
loss = F.binary_cross_entropy(y_pred, Y) # Calcul du coût
all_losses.append(loss.item())
loss.backward() # Magie qui calcule les gradients
# Mise à jour
perceptron.linear.weight.data = perceptron.linear.weight.data - lr * perceptron.linear.weight.grad.data
perceptron.linear.bias.data = perceptron.linear.bias.data - lr * perceptron.linear.bias.grad.data
perceptron.linear.weight.grad.data.zero_() # On doit effacer les anciens gradients
perceptron.linear.bias.grad.data.zero_()
print("Loss final :", loss.item())
print("Parameters :")
print("W :", perceptron.linear.weight.data)
print("Bias :", perceptron.linear.bias.data)
w_1 = perceptron.linear.weight.data[0][0]
w_2 = perceptron.linear.weight.data[0][1]
b = perceptron.linear.bias.data[0]
r = torch.arange(0, 7, 0.1)
fig = go.Figure([
go.Scatter(x=positif_x, y=positif_y, mode="markers", marker=dict(size=10, color="green")), go.Scatter(x=negatif_x, y=negatif_y, mode="markers",
marker=dict(size=10, color="red")),
go.Scatter(x=test_x, y=test_y, mode="markers+text", text=["?"], textposition="top center", marker=dict(size=10, color="blue")),
go.Scatter(x=r, y=(-b + 0.5) / w_2 - w_1 / w_2 * r)])
fig.show()
return all_losses
all_losses = descente_gradient()
Loss final : 0.36282074451446533 Parameters : W : tensor([[0.6369, 0.5167]]) Bias : tensor([-2.9017])
# Il est souvent utile de visualiser l'évolution du loss pour vérifier que l'on converge
px.line(x=range(len(all_losses)), y=all_losses)
def descente_gradient_divergent():
perceptron = Perceptron2(2, 1)
lr = 1
X = torch.Tensor([list(positif_x) + list(negatif_x), list(positif_y) + list(negatif_y)]).T
Y = torch.Tensor([1 for _ in range(len(positif_x))] + [0 for _ in range(len(negatif_x))]).reshape(-1, 1)
all_losses = []
for _ in range(100):
y_pred = perceptron(X)
loss = F.binary_cross_entropy(y_pred, Y) # Calcul du coût
all_losses.append(loss.item())
loss.backward() # Magie qui calcule les gradients
# Mise à jour
perceptron.linear.weight.data = perceptron.linear.weight.data - lr * perceptron.linear.weight.grad.data
perceptron.linear.bias.data = perceptron.linear.bias.data - lr * perceptron.linear.bias.grad.data
perceptron.linear.weight.grad.data.zero_() # On doit effacer les anciens gradients
perceptron.linear.bias.grad.data.zero_()
print("Loss final :", loss.item())
print("Parameters :")
print("W :", perceptron.linear.weight.data)
print("Bias :", perceptron.linear.bias.data)
w_1 = perceptron.linear.weight.data[0][0]
w_2 = perceptron.linear.weight.data[0][1]
b = perceptron.linear.bias.data[0]
r = torch.arange(0, 7, 0.1)
fig = go.Figure([
go.Scatter(x=positif_x, y=positif_y, mode="markers", marker=dict(size=10, color="green")), go.Scatter(x=negatif_x, y=negatif_y, mode="markers",
marker=dict(size=10, color="red")),
go.Scatter(x=test_x, y=test_y, mode="markers+text", text=["?"], textposition="top center", marker=dict(size=10, color="blue")),
go.Scatter(x=r, y=(-b + 0.5) / w_2 - w_1 / w_2 * r)])
fig.show()
return all_losses
all_losses = descente_gradient_divergent()
Loss final : 0.4014516770839691 Parameters : W : tensor([[0.5419, 0.3781]]) Bias : tensor([-2.9351])
# Il est souvent utile de visualiser l'évolution du loss pour vérifier que l'on converge
px.line(x=range(len(all_losses)), y=all_losses)
Descente de gradient et taille du jeu de données¶
Dans la descente de gradient, le gradient $\frac{\partial J(W)}{\partial W}$ est calculé pour la fonction de coût empirique : il est donc calculé à partir des données. Cependant, quand le jeu de données est trop grand, le calcul du gradient devient trop long, et donc la convergence va être compliquée à atteindre dans un temps raisonnable.
On va donc devoir se contenter d'une approximation très efficace en pratique qui n'utilise qu'une partie du jeu de données pour calculer le gradient : la descente de gradient stochastique (stochastic gradient descent, SGD).
La descente de gradient stochastique¶
Algorithme
- Initialiser les points $W$ de manière aléatoire (souvent une gaussienne centrée sur 0)
- Découper le dataset en morceau de taille fixée appelées les batchs.
- Jusqu'à la convergence ou nombre d'itération maximal:
- Pour chaque batch
- Calcul du gradient $\frac{\partial J(W)}{\partial W}$ sur le batch
- Mise à jour des poids $W \leftarrow W - \eta\frac{\partial J(W)}{\partial W}$
- Pour chaque batch
- Retourner les poids
Backpropagation¶
Calculer les gradients¶
Pour que la descente de gradient fonctionne, il est crucial de pouvoir calculer des gradients, c'est à dire la dérivée de la fonction de coût à chaque étape.
Exemple simple¶
Exemple¶

$$ \begin{align} J(W) &= -(y * log(f(x; W)) + (1 - y) * log(1 - f(x; W))\\ &= -(y * log(\sigma(\sigma(x * w_1)*w_2)) + (1 - y) * log(1 - \sigma(\sigma(x * w_1)*w_2)) \end{align}$$
Que vaut $\frac{\partial J(W)}{\partial w_1}$ ? $\frac{\partial J(W)}{\partial w_2}$ ? Bon courage tel quel, même avec un exemple facile.
Exemple - La dérivation en chaîne¶
Heureusement, des outils mathématiques nous facilitent la vie.

$$\frac{\partial J(W)}{\partial w_2} = \frac{\partial J(W)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial w_2}$$
$$ \begin{align} J(W) &= -(y * log(f(x; W)) + (1 - y) * log(1 - f(x; W))\\ &= -(y * log(\hat{y})) + (1 - y) * log(1 - \hat{y})\\ \end{align}$$
Exemple - La dérivation en chaîne¶

$$\frac{\partial J(W)}{\partial w_2} = \frac{\partial J(W)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial w_2}$$
$$ \begin{align} \frac{\partial J(W)}{\partial \hat{y}} = -(\frac{y}{\hat{y}} - \frac{1-y}{1-\hat{y}}) \end{align}$$
$$[f(g(x))]' = f'(g(x))*g'(x)$$
Exemple - La dérivation en chaîne¶

$$\frac{\partial J(W)}{\partial w_2} = \frac{\partial J(W)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial w_2}$$
$$ \begin{align} \hat{y} = \sigma(z_1 * w_2) \end{align}$$
Exemple - La dérivation en chaîne¶

$$\frac{\partial J(W)}{\partial w_2} = \frac{\partial J(W)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial w_2}$$
$$ \begin{align} \frac{\partial \hat{y}}{\partial w_2} = z_1 * (\sigma(z_1 * w_2)(1-\sigma(z_1 * w_2))) \end{align}$$
Et voilà !
Exemple - La dérivation en chaîne¶

Calculons la dérivée suivante : $\frac{\partial J(W)}{\partial w_1} = \frac{\partial J(W)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z_1}\frac{\partial z_1}{\partial w_1}$
Une partie ($\frac{\partial J(W)}{\partial \hat{y}}$) a déjà été calculée !
$$ \frac{\partial \hat{y}}{\partial z_1} = w_2 * (\sigma(z_1 * w_2)(1-\sigma(z_1 * w_2))) $$
$$ \frac{\partial z_1}{\partial w_1} = w_1 * (\sigma(x_1 * w_1)(1-\sigma(x_1 * w_1))) $$
Exemple - De quoi a-t'on besoin pour calculer la valeur des dérivées ?¶
$$\frac{d\hat{y}}{dw_2} = z_1 * (\sigma(z_1 * w_2)(1-\sigma(z_1 * w_2)))$$
- La valeur actuelle de $W$, i.e. $w_1$ et $w_2$.
- Des valeurs pour $y$, $\hat{y}$, $z_1$, et $x_1$. On obtient ces valeurs depuis de vraies données !
Exemple - Forward propagation¶

Exemple - Forward propagation¶

Exemple - Forward propagation¶

Exemple - Forward propagation¶

Exemple - Back propagation¶
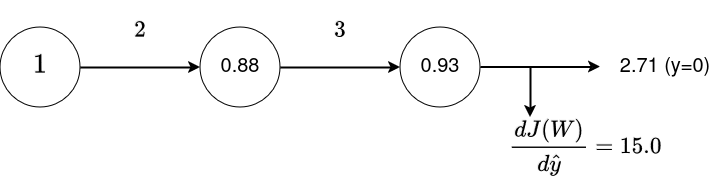
Exemple - Back propagation¶

Exemple - Back propagation¶
$$\frac{dJ(W)}{dw_2} = \frac{dJ(W)}{d\hat{y}}\frac{d\hat{y}}{dw_2} = 0.8223$$
$$\frac{dJ(W)}{dw_1} = \frac{dJ(W)}{d\hat{y}}\frac{d\hat{y}}{dz_1}\frac{dz_1}{dw_1} = 0.2940$$
# On retrouve bien les mêmes résultats
x = torch.Tensor([1])
y = torch.Tensor([0])
w_1 = torch.Tensor([2])
w_2 = torch.Tensor([3])
z = torch.sigmoid(x * w_1)
print("z :", z)
y_hat = torch.sigmoid(z * w_2)
print("y_hat :", y_hat)
J = -torch.log(1 - y_hat)
print("J :", J)
dJ_dy_hat = 1.0 / (1.0 - y_hat)
print("dJ_dy_hat :", dJ_dy_hat)
dy_hat_dz = w_2 * (torch.sigmoid(z * w_2) * (1 - torch.sigmoid(z * w_2)))
print("dy_hat_dz: ", dy_hat_dz)
dy_hat_dw_2 = z * (torch.sigmoid(z * w_2) * (1 - torch.sigmoid(z * w_2)))
print("dy_hat_dw_2: ", dy_hat_dw_2)
dz_dw_1 = x * (torch.sigmoid(x * w_1) * (1 - torch.sigmoid(x * w_1)))
print("dz_dw_1: ", dz_dw_1)
# On recombine tout
d_J_dw_1 = dJ_dy_hat * dy_hat_dz * dz_dw_1
print("d_J_dw_1 :", d_J_dw_1)
d_J_dw_2 = dJ_dy_hat * dy_hat_dw_2
print("d_J_dw_2 :", d_J_dw_2)
z : tensor([0.8808]) y_hat : tensor([0.9335]) J : tensor([2.7112]) dJ_dy_hat : tensor([15.0467]) dy_hat_dz: tensor([0.1861]) dy_hat_dw_2: tensor([0.0546]) dz_dw_1: tensor([0.1050]) d_J_dw_1 : tensor([0.2940]) d_J_dw_2 : tensor([0.8223])
##### On peut directement calculer les gradients avec Torch
y = torch.Tensor([0])
w_1 = torch.Tensor([2])
w_1.requires_grad_()
w_2 = torch.Tensor([3])
w_2.requires_grad_()
z = torch.sigmoid(x * w_1)
y_hat = torch.sigmoid(z * w_2)
J = -torch.log(1 - y_hat)
J.backward()
print("d_J_dw_1 :", w_1.grad)
print("d_J_dw_2 :", w_2.grad)
d_J_dw_1 : tensor([0.2940]) d_J_dw_2 : tensor([0.8223])
- Pourquoi ça marche ? Quelqu'un a écrit la dérivée pour nous.
Graphe de calculs¶
Graphe de calculs / Computational Graph¶
Pour généraliser notre exemple, il nous faut une structure de donnée qui représente les calculs et leur ordre dans le réseau de neurone : c'est ce qu'on appelle le graphe de calculs (computational graph).
Toutes les bibliothèques de deep learning sont basées sur la notion de computational graph.
Notre représentation visuelle du perceptron et du perceptron multi-couche est un graphe de calcul où l'on a caché les sommes et les sigmoïd !
Graphe de calculs / Computational Graph - Définition¶
Un graphe de calculs est un graphe acyclique où chaque nœud (aussi appelés porte) représente une opération permettant de transformer les entrées en des sorties.
Voici une exemple de graphe permettant de faire le calcul $f(x, y, z) = (x + y) * z$ :
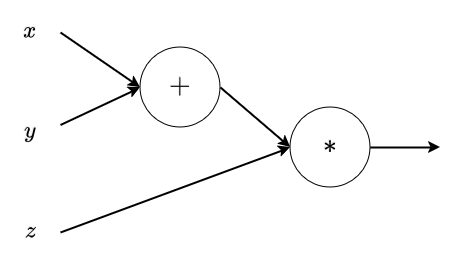
Forward propagation dans un graphe de calcul¶
Étant donné un graphe de calcul, nous pouvons calculer sa sortie en propageant les entrées aux différents nœuds suivant l'ordre topologique (i.e. suivant la distance maximale de chaque nœud à une entrée). (ici, u=x+y, v=f=u*z)
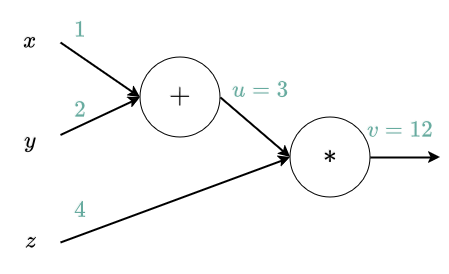
Backward propagation dans un graphe de calcul¶
Nous voulons maintenant calculer la dérivée de notre fonction représentée par le graphe en fonction des entrées. Pour cela nous pouvons utiliser la dérivation en chaîne. En faisant cela, nous remarquons que nous avons besoin des dérivées en fonctions des variables intermédiaires.
Pendant la backward propagation, nous parcourons le graphe dans l'inverse de l'ordre topologique et, pour chaque variable intermédiaire, nous calculons le gradient en fonction des gradients déjà calculés.
La backward propagation doit obligatoirement se faire après la forward propagation.
Exemple¶
$$\frac{\partial f}{\partial f} = 1$$ $$\frac{\partial f}{\partial u} = z$$ ($f=u*z$) $$\frac{\partial f}{\partial z} = u$$ $$\frac{\partial u}{\partial x} = 1$$ ($u=x+y$) $$\frac{\partial u}{\partial y} = 1$$ $$\frac{\partial f}{\partial x} = \frac{\partial f}{\partial u} \frac{\partial u}{\partial x}$$ $$\frac{\partial f}{\partial y} = \frac{\partial f}{\partial u} \frac{\partial u}{\partial y}$$
Exemple¶
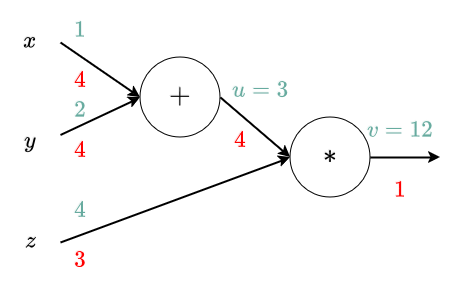
Zoom sur une porte à une entrée (x), une sortie (y)¶
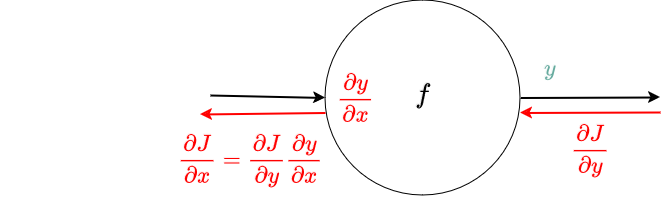
Zoom sur une porte à deux entrées (x, y), une sortie (z)¶
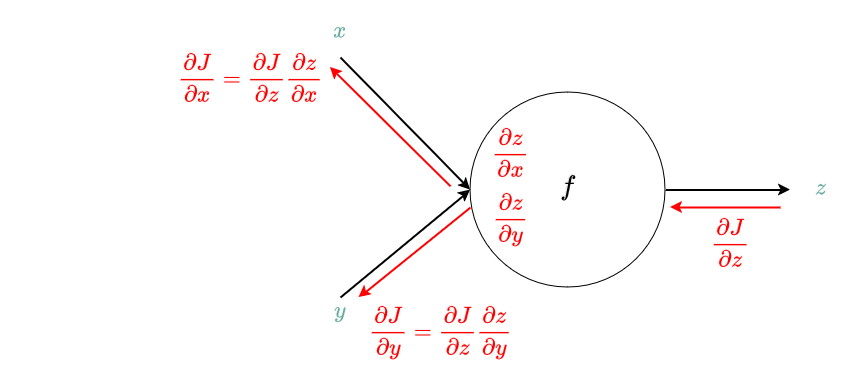
Zoom sur une porte à une entrée (x), deux sorties (y, z)¶
Nous avons ici une variante de la dérivation chainée : l'entrée hérite du gradient de chacune des sorties !
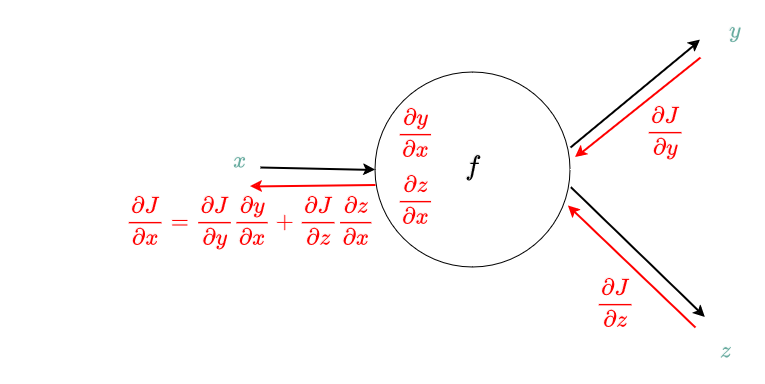
Cas particuliers¶
- La porte addition $f(x, y) = x + y$ : Distribue le gradient équitablement entre toutes les sorties
- La porte multiplication $f(x, y) = x * y$ : Multiplie le gradient par l'autre entrée
- La porte copy (copie l'entrée dans deux sortie) $f(x) = \begin{bmatrix} x \\ x \end{bmatrix}$: Ajoute les gradients
- La porte maximum $f(x, y) = max(x, y)$ : Dirige le gradient vers l'entrée max, l'autre a un gradient à 0.
Backpropagation - L'intuition¶
- On mesure une erreur en sortie : $L(\hat y, y)$.
- On transforme cette erreur en signal de blâme local (sortie binaire) : $\delta = \hat y - y$.
- On remonte couche par couche : chaque neurone transmet une part du blâme selon son poids et la pente locale $g'(z)$.
- Chaque poids est corrigé pour réduire l’erreur : $\Delta w \propto -\frac{\partial L}{\partial w}$.
La backpropagation¶
Algorithme
- Pour chaque porte du graphe, prises suivant l'ordre topologique
- Récupérer les entrées (existent à cause de l'ordre topologique)
- Calculer la sortie de la porte
- Enregistrer les éléments servant à calculer le gradient
- Pour chaque porte du graphe prises suivant l'ordre topologique inverse
- Récupérer le gradient des portes suivantes (1 si c'est la dernière porte)
- Propager le gradient aux entrées
Exemple - Avec le perceptron¶
Calculer les gradients en fonction des entrées valant $(1, 2, -2)$. On a considéré que les poids étaient égaux à 1.
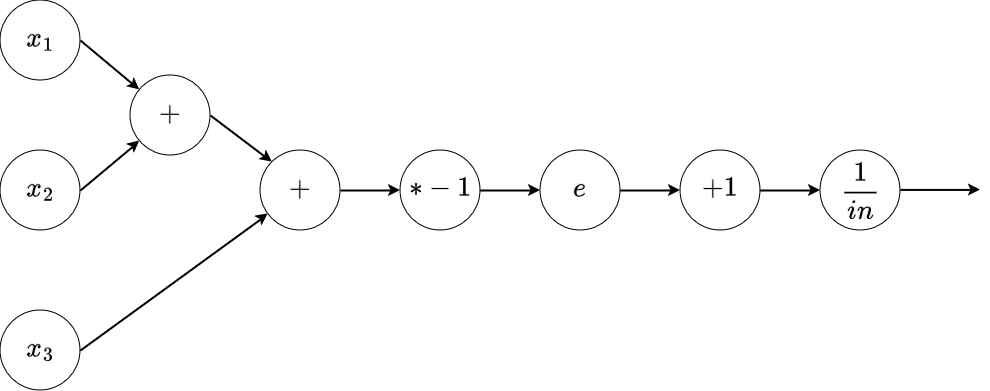
Exemple - Avec le perceptron¶
Calculer les gradients en fonction des entrées valant $(1, 2, -2)$. On a considéré que les poids étaient égaux à 1.
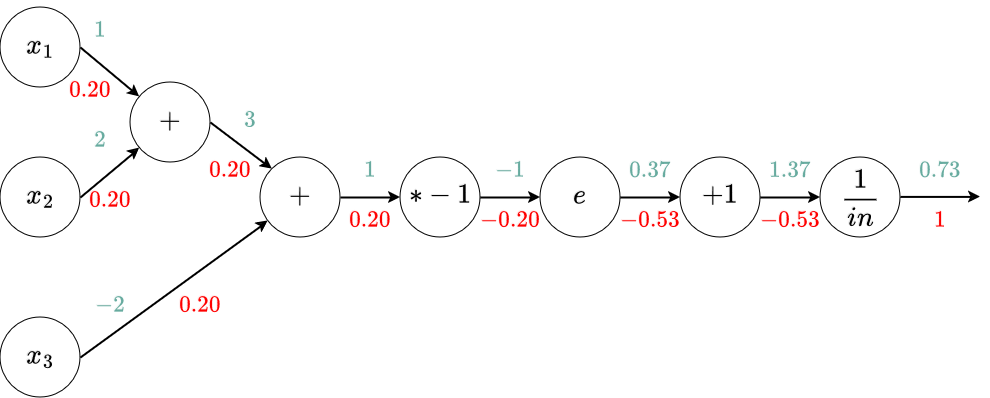
x = torch.Tensor([1, 2, -2])
x.requires_grad_()
y = x.sum()
z = 1.0 / (1 + torch.exp(-y))
z.backward()
x.grad
tensor([0.1966, 0.1966, 0.1966])
# En Torch, les portes implémentent torch.autograd.Function
class Multiply(torch.autograd.Function):
@staticmethod
def forward(ctx, x, y):
ctx.save_for_backward(x, y)
z = x * y
return z
def backward(ctx, grad_z):
x, y = ctx.saved_tensors
grad_x = y * grad_z
grad_y = x * grad_z
return grad_x, grad_y
x, y = torch.Tensor([1]), torch.Tensor([2])
x.requires_grad_()
y.requires_grad_()
z = Multiply.apply(x, y)
print("Output", z)
z.backward(torch.Tensor([3]))
print("Gradients :", x.grad, "et", y.grad)
Output tensor([2.], grad_fn=<MultiplyBackward>) Gradients : tensor([6.]) et tensor([3.])
Remarques sur la back propagation¶
- En pratique, nous voulons le gradient par rapport aux poids du modèle. On considère que les poids sont des entrées de notre graphe de calculs et on utilise la back propagation de la même manière.
- Pour que la backpropagation fonctionne, il faut que nos fonctions soit dérivables au moins pour les points données en entrée ! Quand la fonction n'est pas dérivable en quelques points précis, on peut s'arranger en donnant une valeur arbitraire (par exemple, la fonction max en 0).
# Comportement de la fonction max en Torch
x, y = torch.Tensor([1]), torch.Tensor([0])
x.requires_grad_()
torch.max(x, y).backward()
print("Pour x > y :", x.grad)
x = torch.Tensor([-1])
x.requires_grad_()
torch.max(x, y).backward()
print("Pour x < y :", x.grad)
x = torch.Tensor([0])
x.requires_grad_()
torch.max(x, y).backward()
print("Pour x = y :", x.grad)
Pour x > y : tensor([1.]) Pour x < y : tensor([0.]) Pour x = y : tensor([0.5000])
Remarques sur la back propagation¶
- Gradient sur un batch : On additionne les gradients de tous les points dans le jeu de données !
- Conséquence importante : Après un batch, il faut remettre les gradients à 0.
# On fait passer deux fois les entrées dans la fonction
x, y = torch.Tensor([1]), torch.Tensor([2])
x.requires_grad_()
y.requires_grad_()
z = Multiply.apply(x, y)
print("Output :", z)
z.backward(torch.Tensor([3]))
print("Gradients :", x.grad, "et", y.grad)
z = Multiply.apply(x, y)
print("Output 2 :", z)
z.backward(torch.Tensor([3]))
print("Gradients 2 :", x.grad, "et", y.grad)
Output : tensor([2.], grad_fn=<MultiplyBackward>) Gradients : tensor([6.]) et tensor([3.]) Output 2 : tensor([2.], grad_fn=<MultiplyBackward>) Gradients 2 : tensor([12.]) et tensor([6.])
Généralisation de la back propagation¶
La back propagation se généralise à des vecteurs ou matrices en entrées. Dans ce cas, nous manipulons des gradients (plusieurs entrées) et des matrices Jacobiens (plusieurs entrées et sortie).
Résumé¶
- Le multi-layer perceptron
- Fonctions d'activation
- Fonctions de coût
- Forward pass
- Descente de gradient
- Backpropagation