1 Introduction

Le but de cet exercice est de :

1. Manipuler les vecteurs de la STL en codant un simulateur du jeu de cartes 6 qui prend. Ce simulateur permet de faire des statistiques sur différentes stratégies de jeu. Peut-être vous permettra-t-il de gagner vos prochaines parties ?
2. Adopter une démarche “Développement piloté par les tests” (Tests-Driven Development - TDD) pour certains des codes que vous allez écrire.
3. Découvrir l’environnement de tests GoogleTest que nous utiliserons pour les tests unitaires de cette UV.
4. Faire des optimisations de code en s’appuyant sur un profiler de code.

---- Statistiques (sur 10000 simulations) ----
Nom strategie                  | Moyenne rangs | Moyenne vaches encaissees
Carte la plus petite           |       5.73275 |                        15
Carte au milieu de la main     |       5.39285 |                        14
Carte random                   |       5.99605 |                        16
Carte avant la plus grande     |       5.42985 |                        14
Carte la plus grande           |       4.94850 |                        13

Téléchargez l’archive SixQuiPrend.zip dans le répertoire de votre choix et exploitez-la selon la procédure cmake de ce document.

Dans la suite, vous travaillez essentiellement sur les fichiers src/core/simulateur.cpp et src/core/simulateur.h.

2 Étapes d’une partie de “6 qui prend” et rôle des différentes variables du programme

Au début d’une partie, la variable tas_cartes_initial contient kNb_initial_cartes_en_main numérotées de 1 à kNb_initial_cartes_en_main et mélangées :

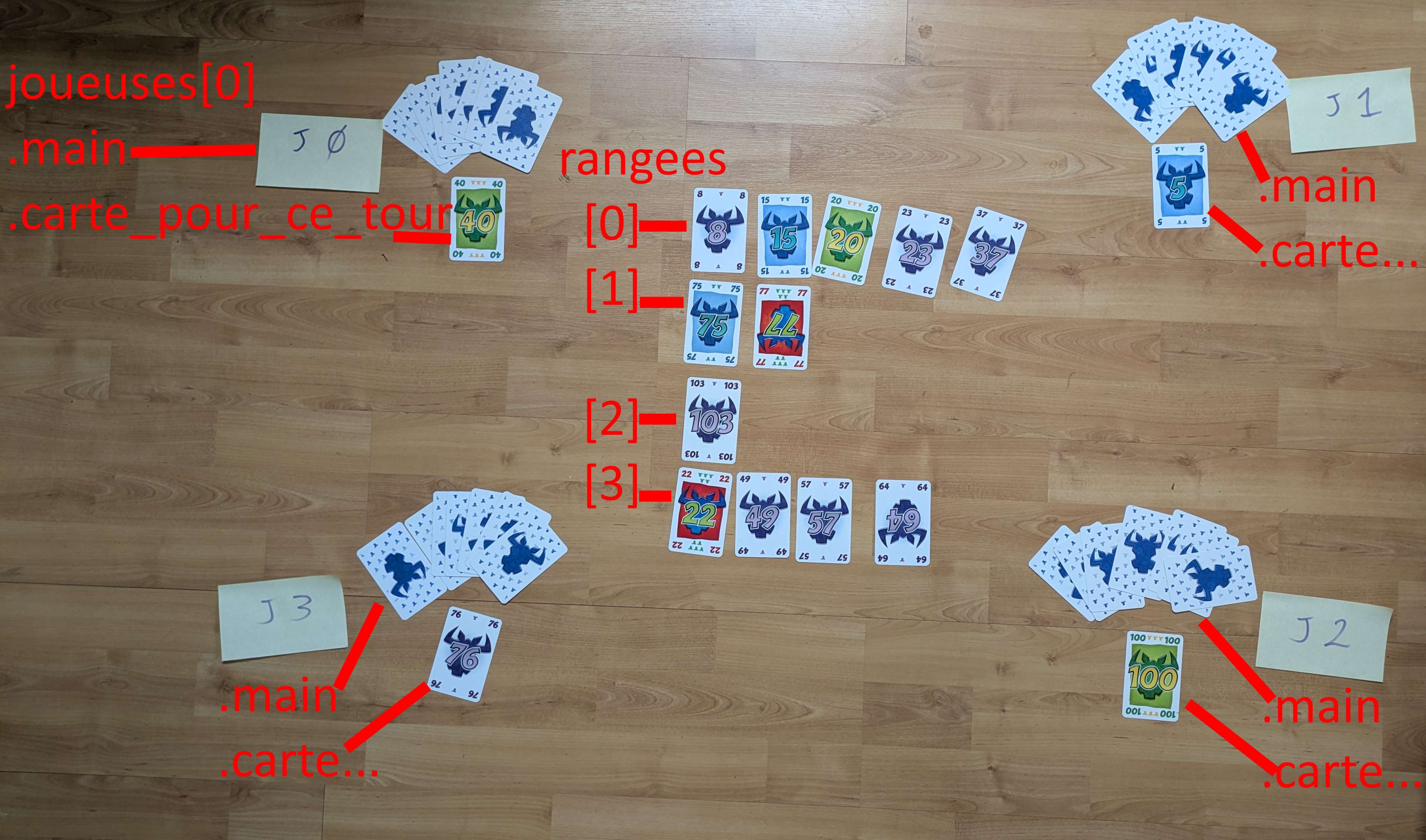
Après distribution, chaque main de joueur·se contient kNb_initial_cartes_en_main cartes en provenance de tas_cartes_initial. Par ailleurs, kNb_rangees rangées sont initialisées chacune avec une carte provenant de tas_cartes_initial. Dans la figure ci-après :

• Ne figurent que 4 joueurs·ses.
• Les rangées contiennent respectivement la carte 8, la carte 75, la carte 103 et la carte 22.

Supposons que nous sommes parvenus au 3^ème tour de jeu. joueuse[0] a décidé de jouer sa carte 40, joueuse[1] la 5, joueuse[2] la 100 et joueuse[3] la 76. rangees[0] contient les cartes 8, 15, 20, 23 et 27, tandis que rangees[1] contient 75 et 77, etc.

Durant chaque tour, les joueurs·ses jouent dans l’ordre croissant des cartes qu’iels ont décidé de jouer. Donc, l’ordre de passage des joueurs·ses pour ce 3^ème tour est joueuse[1] (carte 5), joueuse[0] (carte 40), joueuse[3] (carte 77) et joueuse[3] (carte 100). joueuse[1] ne peut ajouter sa carte à une rangée, vu que sa valeur est inférieure à la carte à droite de chaque rangée. Dans la simulation, joueuse[1] choisit systématiquement de ramasser la rangée qui lui apporte le moins de vaches (symboles en haut et de chaque rangée). Ramasser rangees[0] lui infligerait une pénalité de 8 vaches, rangees[1] 7 vaches, rangees[2] 1 vaches, et rangees[3] 8 vaches. joueuse[1] ramasse donc rangees[2] et y met sa carte.

C’est au tour de joueuse[0]. Iel doit jouer dans rangees[0] qui a déjà kNb_max_cartes_dans_rangee. joueuse[0] ramasse rangees[2] et y met sa carte.

3 Initialisations du simulateur (Distribution des cartes) (0h20)

3.1 Marque TODO 1

Dans simuler_partie(statistiques_t& stat), définissez tas_cartes_initial en tant que std::vector<int> contenant 104 valeurs et stockez-y des valeurs allant de 1 à 104.

Complétez la fonction dump_cartes() (cf. marque TODO 1 bis) pour qu’elle affiche les valeurs stockées dans le vecteur v passé en paramètre. Avec dump_cartes(), vérifiez que tas_cartes_initial est correctement initialisé. NB : Si vous souhaitez que vos entiers soient systématiquement affichés sur 3 caractères et cadrés à droite, utilisez cout << format("{:3} ", valeur_a_afficher);

Mélangez tas_cartes_initial et vérifiez le mélange avec dump_cartes().

3.2 Marque TODO 2

Initialisez maintenant le tableau joueuses pour les kNb_joueuses qui seront simulées :

• La première joueuse reçoit, pour sa main, les 10 premières cartes de tas_cartes_initial, la deuxième, les 10 suivantes, etc.
• Pensez à trier la main et à l’afficher avec dump_cartes() pour vérifier que les mains ont été correctement initialisées.
• La stratégie de la joueuse i est initialisée à strategie_joueuses[i].

3.3 Marque TODO 3

Initialisez les kNb_rangees de rangees. Affichez-les avec dump_cartes() pour vérifier que votre code est correct.

4 Simulation des tours de jeu (0h20)

4.1 Marque TODO 4

• Pour chaque joueuse, appelez choisir_carte() (que nous coderons plus tard).
• Au niveau de la déclaration de choisir_carte() dans simulateur.h (marque TODO 4 bis) et, pour être cohérent·e, au niveau de sa définition dans simulateur.cpp (marque TODO 4 ter), décidez si le paramètre est passé en copie, en référence ou en référence constante.

4.2 Marque TODO 5

• Triez joueuses par ordre croissant de l’attribut carte_pour_ce_tour de chaque joueuse.

4.3 Marque TODO 6

• Pour chaque joueuse, appelez jouer_carte() (que nous coderons plus tard).
• Au niveau de la déclaration de jouer_carte() dans simulateur.h (marque TODO 6 bis) et, pour être cohérent·e, au niveau de sa définition dans simulateur.cpp (marque TODO 6 ter), décidez si :
  • le paramètre j est passé en copie, en référence ou en référence constante.
  • le paramètre rangees est passé en copie, en référence ou en référence constante.

4.4 Marque TODO 7

• Recopiez cette instruction : cout << "*** Etat a la fin du tour " << tour << endl;
• Derrière cette instruction, codez l’affichage de la main des différentes joueuses et des cartes dans chaque rangée.

5 Travail concernant la fin de partie (0h10)

5.1 Marque TODO 8

• Triez joueuses par ordre croissant de l’attribut nb_vaches_encaissees de chaque joueuse.
• Derrière cette instruction de tri, recopiez les lignes suivantes :

  cout << "Classement des joueuses en fonction du nombre de vaches encaissees"
       << endl;
  int classement{0};
  int dernier_nb_vaches_encaissees{-1};
  int nb_joueuses_classees{0};
  for (const auto &j : joueuses) {
    ++nb_joueuses_classees;
    if (dernier_nb_vaches_encaissees < j.nb_vaches_encaissees) {
      // La joueuse j n'est pas ex-aequo avec la joueuse precedente (ou bien c'est la premiere joueuse au classement)
      classement = nb_joueuses_classees;
      dernier_nb_vaches_encaissees = j.nb_vaches_encaissees;
    }
    cout << std::format("{:3} vaches encaissees (Strategie {})", j.nb_vaches_encaissees,
                        get_nom_strategie(j.strategie))
         << endl;
    stat[j.strategie].first += classement;
    stat[j.strategie].second += j.nb_vaches_encaissees;
  }

La fin de votre affichage devrait être désormais :

Classement des joueuses en fonction du nombre de vaches encaissees
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)
  0 vaches encaissees (Strategie Carte la plus petite)

Cet affichage n’est pas pertinent, car il vous manque encore le code de 4 fonctions. C’est l’objet de la prochaine section.

6 Codage des fonctions manquantes (0h20)

Dans cette section, nous implantons get_nb_vaches(const cartes_t& cartes), choix_carte(), jouer_carte(), et get_rang_ou_jouer() (dans cet ordre, pour aller de la plus simple à la plus compliquée à coder).

6.1 Développement piloté par les tests (Tests-Driven Development - TDD) avec GoogleTest

Nous appliquons ici la même démarche que celle vue dans le Devoir Hors Présentiel de CSC4103 :

• Pour chaque fonction à coder, des tests unitaires ont été préalablement développés.
• Tous ces tests sont, pour l’instant, faux, vu que les fonctions testées dont vides.
• Quand vous codez une fonction, vous passez ses tests pour vérifier que votre code est correct.
• Une fois que les tests passent, vous pouvez implanter une autre fonction.

Pour ces tests comme pour tous les tests unitaires en C++ de cette UV, nous utilisons GoogleTest.

Suivez la procédure GoogleTest de ce document pour vérifier le résultat des tests fournis dans src/test/unitTests.cpp. Sur les 14 tests effectés, seul 1 est correct. Il concerne la fonction get_nb_vaches(int carte) dont le code vous est déjà fourni, car il n’apportait rien du point de vue manipulation des vecteurs.

6.2 get_nb_vaches(const cartes_t& cartes)

Voyons tout d’abord comment est codé le test de cette fonction. Dans src/test/unitTests.cpp, vous trouvez les lignes :

TEST(get_nb_vaches, cartes) {
  const cartes_t cartes{1, 15, 20, 44, 55, 104};
  EXPECT_EQ(19, get_nb_vaches(cartes));
}

• TEST(get_nb_vaches, ...) est le nom de la fonction concernée par ce test.
• TEST(..., cartes) désigne le sous-cas testé par ce test (ici, plusieurs cartes).
• const cartes_t cartes{1, 15, 20, 44, 55, 104}; est notre jeu de données d’entrée. Dans le cas présent, c’est un ensemble cartes de cartes dont on cherche à connaître le nombre total de vaches.
• EXPECT_EQ(19, get_nb_vaches(cartes)); est le test lui-même :
  • EXPECT_EQ désigne un test d’égalité. En cas d’erreur, GoogleTest affichera les deux termes de EXPECT_EQ.
  • EXPECT_EQ(19, ...) est la valeur attendue pour ce test.
  • EXPECT_EQ(..., get_nb_vaches(cartes)) fait l’appel à la fonction testée get_nb_vaches() avec cartes en paramètre. La valeur renvoyée par cette fonction est la valeur observée pour ce test et est comparée à la valeur attendue (19).

6.2.1 Marque TODO 9

• Pour chaque carte de cartes, appelez get_nb_vaches(int carte) (qui est fournie).
• Retournez la somme des valeurs obtenues.
• Vérifiez que le test unitaire TEST(get_nb_vaches, cartes) est désormais correct.

6.3 choix_carte()

Comme cette fonction simule une joueuse choisissant une carte selon une stratégie, il faut tester les différentes stratégies, soit plusieurs tests TEST(choisir_carte, ...). Étudions un exemple de ces tests de stratégie avec ce code issu de src/test/unitTests.cpp :

TEST(choisir_carte, strategie_kCarte_la_plus_petite) {
  Joueuse j{
    strategie_t::kCarte_la_plus_petite,
    {2, 4, 6},
    0,
    {},
    0
  };

  choisir_carte(j);

  EXPECT_EQ(cartes_t({4, 6}), j.main);
  EXPECT_EQ(2, j.carte_pour_ce_tour);
}

• TEST(choisir_carte, strategie_kCarte_la_plus_petite) : Le test concerne la fonction choisir_carte et le sous-cas “Stratégie kCarte_la_plus_petite”.
• Joueuse j{}; est notre jeu de données d’entrée. Dans le cas présent, il est uniquement constituée d’une joueuse j qui n’est pas const, car choisir_carte modifie j.
• choisir_carte(j); invoque la fonction à tester.
• EXPECT_EQ(cartes_t({4, 6}), j.main); définit la valeur attendue cartes_t({4, 6}) pour j.main.
• EXPECT_EQ(2, j.carte_pour_ce_tour); définit la valeur attendue 2 pour j.carte_pour_ce_tour.

6.3.1 Marque TODO 10

• Dans src/test/unitTests.cpp (marque TODO 10 bis), dans le test TEST(choisir_carte, strategie_kCarte_la_plus_grande), remplacez la ligne actuelle EXPECT_TRUE(false); (qui garantit que le test est toujours calculé comme faux) par un test correct de la stratégie kCarte_la_plus_grande.
• Déterminez j.carte_pour_ce_tour en fonction de j.strategie.
  • NB : Dans votre code, profitez du fait que j.main est un vecteur trié.
• Supprimez j.carte_pour_ce_tour de j.main (en veillant à garder j.main trié)
• Vérifiez que les tests unitaires TEST(choisir_carte, ...) sont désormais corrects.

TEST(choisir_carte, strategie_kCarte_la_plus_grande) {
  Joueuse j{
    strategie_t::kCarte_la_plus_grande,
    {2, 4, 6},
    0,
    {},
    0
  };

  choisir_carte(j);

  EXPECT_EQ(cartes_t({2, 4}), j.main);
  EXPECT_EQ(6, j.carte_pour_ce_tour);
}

  case kCarte_la_plus_petite:
    j.carte_pour_ce_tour = j.main.front();
    break;

6.4 get_rang_ou_jouer()

6.4.1 Marque TODO 11

NB : Le codage de cette fonction pourrait vous prendre du temps (car il faut assimiler correctement les règles du “6 qui prend”). Aussi, si vous avez l’impression d’être ou de prendre du retard, n’hésitez pas à copier-coller le code de la solution.

Concevez et plantez l’algorithme pour que cette fonction respecte :

• la section “Chaque carte jouée ne peut convenir qu’à une seule série :” des règles,
• et la section “Carte trop faible” de ces règles (sachant que, pour notre simulateur, nous supposons que leŸma joueur·se choisit systématiquement la rangée où il ramasse le moins de vaches).

Vérifiez que les tests unitaires TEST(get_rang_ou_jouer, ...) sont désormais corrects.

size_t get_rang_ou_jouer(const Joueuse& j, const rangees_t& rangees) {
  // TODO 11

  // Recherche rang tel que j.carte_pour_ce_tour est la plus proche de la
  // derniere carte de la rangee.
  size_t rang_ou_jouer = 0;
  int diff = j.carte_pour_ce_tour - rangees[rang_ou_jouer].back();
  for (size_t r = 1; r < kNb_rangees; ++r) {
    if (0 < j.carte_pour_ce_tour - rangees[r].back() &&
        j.carte_pour_ce_tour - rangees[r].back() < diff) {
      diff = j.carte_pour_ce_tour - rangees[r].back();
      rang_ou_jouer = r;
    }
  }
  if (diff < 0) {
    // La carte jouee est une carte trop faible par rapport aux cartes dans @p
    // rangees
    // ==> On choisit la rangee ou la joueuse encaisse le moins de vaches.
    rang_ou_jouer = 0;
    int encaissement = get_nb_vaches(rangees[rang_ou_jouer]);
    for (size_t r = 1; r < kNb_rangees; ++r) {
      if (get_nb_vaches(rangees[r]) < encaissement) {
        encaissement = get_nb_vaches(rangees[r]);
        rang_ou_jouer = r;
      }
    }
  }
  return rang_ou_jouer;
}

6.5 Fonction jouer_carte()

6.5.1 Marque TODO 12

Après la ligne size_t rang_ou_jouer{get_rang_ou_jouer(j, rangees)}; (déjà fournie) :

• Commencez par traiter le cas où le·la joueur·se encaisse les vaches qui sont dans la rangée où iel joue. Pensez à :
  • mettre à jour j.cartes_encaissees et j.nb_vaches_encaissees.
  • vider les cartes de votre rangée.
• Puis, ajoutez j.carte_pour_ce_tour dans cette rangée.
• Vérifiez que les tests unitaires TEST(jouer_carte, ...) sont désormais corrects.

  if (j.carte_pour_ce_tour < rangees[rang_ou_jouer].back() 
    || rangees[rang_ou_jouer].size() >= kNb_max_cartes_dans_rangee) {

7 Test du code final (0h05)

Vérifiez que votre code fonctionne correctement en l’exécutant et en analysant vos traces.

Puis, dans src/main/main.cpp, remplacez l’instruction simuler_partie(stat); par les lignes :

  for (auto i = 0; i < kNb_simulations; ++i) {
    simuler_partie(stat);
  }

  // Affiche les statistiques.
  cout << format("---- Statistiques (sur {} simulations) ----", kNb_simulations) << endl;
  cout << format("{:30} | {:13} | {:25}", "Nom strategie",
                 "Moyenne rangs",
                 "Moyenne vaches encaissees")
       << endl;
  for (const auto& [strategie, ses_stat] : stat) {
    // Pour la moyenne, on doit diviser par 2 car chaque strategie
    // est testee 2 fois durant chaque simulation de partie.
    cout << format("{:30} | {:13.5f} | {:25}", get_nom_strategie(strategie),
                   static_cast<double>(ses_stat.first) / 2 / kNb_simulations,
                   ses_stat.second / 2 / kNb_simulations)
         << endl;
  }

Vérifiez que les statistiques désormais affichées sont cohérentes avec vos traces.

Puis, faites les modifications suivantes dans src/core/simulateur.cpp :

1. Initialisez kNb_simulations à 10'000 au lieu de 1 (notez que le caractère ' peut servir de séparateur de milliers pour améliorer la lisibilité).
2. Mettez en commentaires toutes les sections de code qui font des appels à dump_cartes() ou des appels à cout. NB : Ne mettez pas en commentaires les cout présents dans src/core/main.cpp vu q’ils affichent les résultats de vos simulations.

Exécutez votre programme pour afficher les statistiques sur 10.000 simulations.

Corrigé (à exploiter selon la procédure cmake de ce document).

8 Profiling du code pour l’optimiser (0h15)

Maintenant que le code est opérationnel, nous allons repérer les sections de code où notre programme passe du temps, afin d’optimiser ces sections de code et donc améliorer le temps d’exécution. Pour ce faire, nous allons utiliser un “profiler de performances” qui nous permet de repérer les sections de code problématiques. Nous modifions le code et utilisons à nouveau le “profiler” pour vérifier le résultat de nos optimisations.

Afin de disposer à la fois d’une version non optimisée et d’une version optimisée de notre code (et ainsi pouvoir comparer les performances des codes réalisés):

• Créez un fichier src/core/simulateur_optimise.cpp en suivant la procédure “IDE CLion ou Visual Studio : Ajout de fichiers source dans un projet généré par cmake” de ce document.
• Recopiez le contenu de src/core/simulateur.cpp dans src/core/simulateur_optimise.cpp.
  • NB : Nous verrons plus tard dans cette section que nous aurions pu aussi continuer à travailler sur src/code/simulateur.cpp, mais en utilisant un flag de compilation SIMULATEUR_OPTIMISE. Nous ne le faisons pas pour src/core/simulateur.cpp afin de ne pas alourdir le code avec des #ifdef. Toutefois, nous le ferons pour src/core/simulateur.h et src/test/unitTests.cpp.
• Remplacez le contenu de src/core/CMakeLists.txt (qui, exceptionnellement, n’a pas été correctement modifié par votre IDE) par les lignes :

add_library(lib_core
  simulateur.cpp
  simulateur.h
)

target_include_directories(lib_core PUBLIC ./)

add_library(lib_core_optimise
  simulateur_optimise.cpp
  simulateur.h
)

target_include_directories(lib_core PUBLIC ./)

• Modifiez src/main/CMakeLists.txt pour qu’il ait le contenu suivant :

add_executable(main
  main.cpp
)

target_link_libraries(main lib_core)

add_executable(main_optimise
  main.cpp
)

target_link_libraries(main_optimise lib_core_optimise)

Dans la suite de cette section, vous travaillerez sur src/core/simulateur_optimise.cpp.

Commencez par vérifier que :

1. kNb_simulations est initialisé à 10'000 au lieu de 1.
2. Toutes les sections de code qui font des appels à dump_cartes() ou des appels à cout sont commentées.

Lancez une session de profiling de CPU de six_qui_prend_optimise conformément aux instructions pour Visual Studio ou celles pour CLion. En résumé, pour Visual Studio :

• Configurez votre solution en mode Release (cf. section “Génération d’une version Release d’un programme” de ce document et exécutez votre application dans ce mode.
• Suivez maintenant la section “Profileur de performances” de ce document.

Dans la suite, nous supposons une session de profiling avec Visual Studio.

Votre programme s’exécute, puis Visual Studio affiche le rapport de sa session de diagnostic :

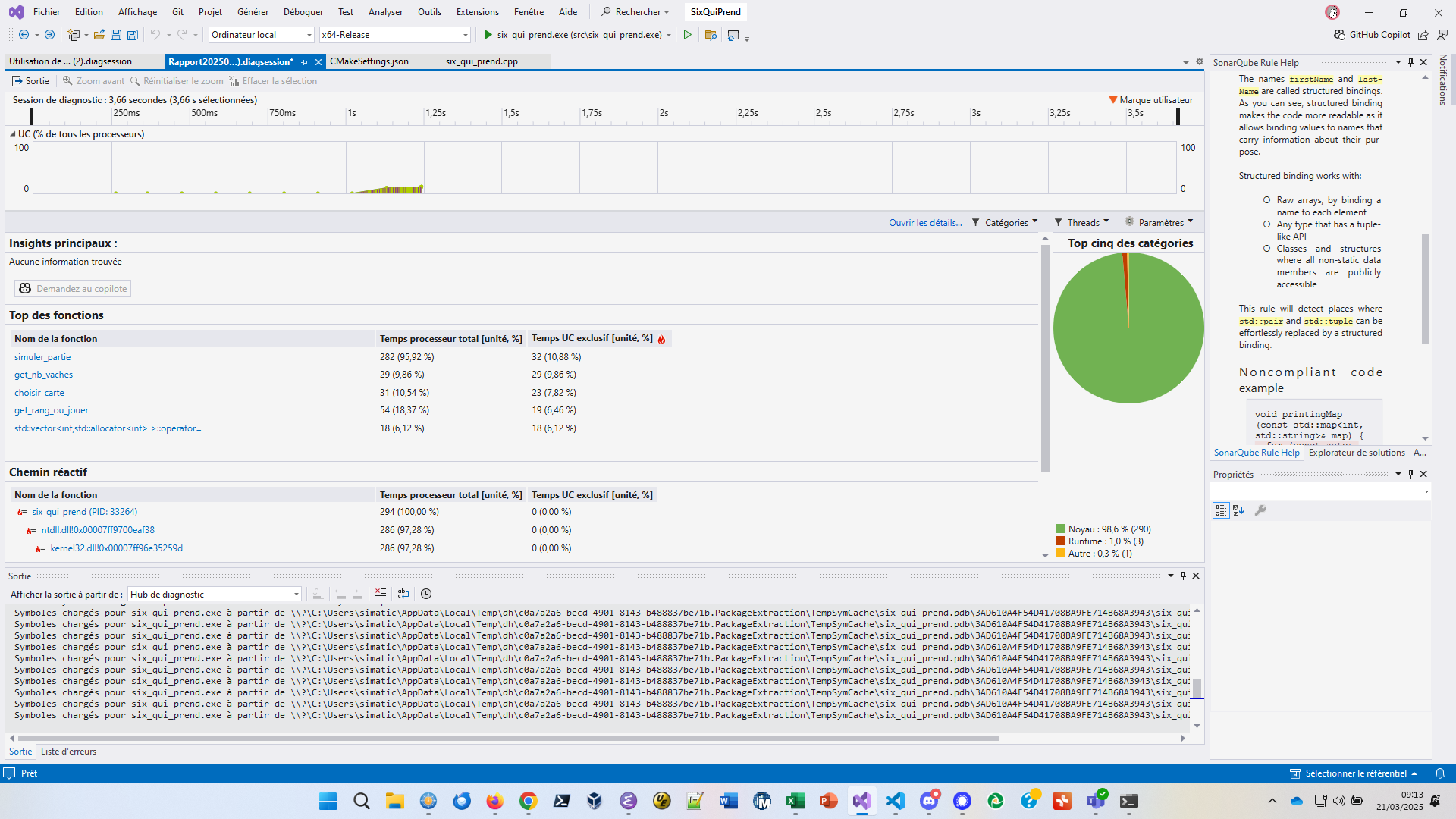
Sans surprise, simuler_partie() représente 95,92% de la consommation CPU totale (colonne “Temps processeur total (unité, %)”). Toutefois, sa colonne “Temps UC exclusif (unité, %)” qui représente la CPU consommée exclusivement dans simuler_partie() proprement dite et non dans les fonctions qu’elle appelle n’est que de 10,88%. Aussi, regardons les autres fonctions signalées dans le rapport :

• get_nb_vaches() représente exclusivement 9,86%.
• choisir_carte() représente exclusivement 7,82%.

Cliquez sur get_nb_vaches. Une fenêtre de diagnostic concernant get_nb_vaches(int carte) s’affiche :

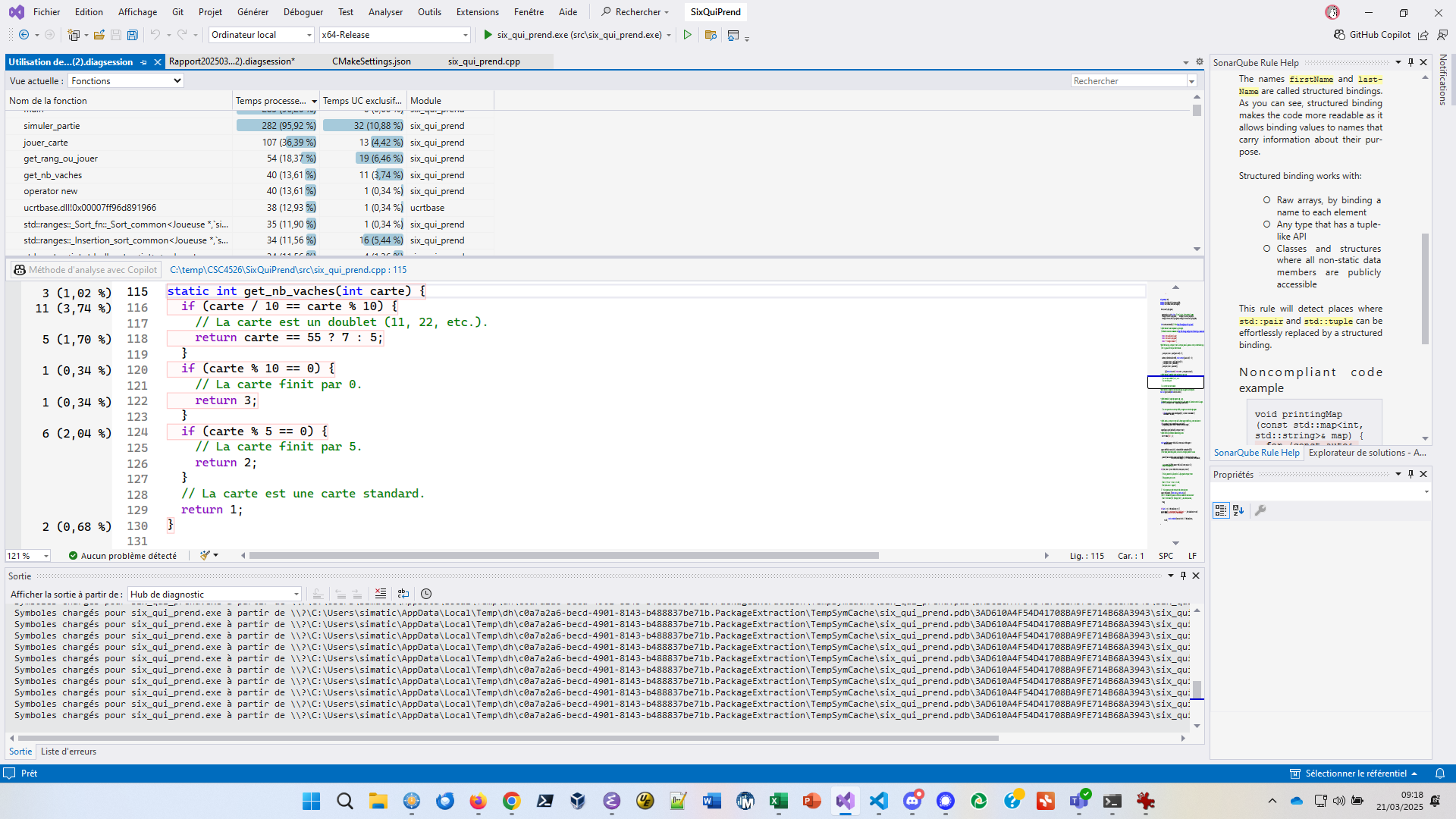
Les différents tests effectués dans cette fonction représentent 10% de l’ensemble de la CPU du programme ! Que proposez-vous pour réduire drastiquement ce pourcentage ?

NB : Si vous souhaitez vérifier, avec les tests GoogleTest, que vos modifications sont correctes, pensez à modifier src/test/CmakeLists.txt pour remplacer sa ligne target_link_libraries(tests GTest::gtest_main lib_simulateur) par target_link_libraries(tests GTest::gtest_main lib_simulateur_optimise) pour tester la version optimisée de votre bibliothèque.

// Pensez a ajouter #include <array>

int get_nb_vaches(int carte) {
  static array<int, kNb_total_cartes + 1> carte2nb_vaches{
                       -1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 3, 5, 1, 1, 1, 2, 1, 1, 1,
                        1, 3, 1, 5, 1, 1, 2, 1, 1, 1, 1, 3, 1, 1, 5, 1, 2, 1,
                        1, 1, 1, 3, 1, 1, 1, 5, 2, 1, 1, 1, 1, 3, 1, 1, 1, 1,
                        7, 1, 1, 1, 1, 3, 1, 1, 1, 1, 2, 5, 1, 1, 1, 3, 1, 1,
                        1, 1, 2, 1, 5, 1, 1, 3, 1, 1, 1, 1, 2, 1, 1, 5, 1, 3,
                        1, 1, 1, 1, 2, 1, 1, 1, 5, 3, 1, 1, 1, 1};
  return carte2nb_vaches[carte];
}

Dans la fenêtre de diagnostic initial, cliquez maintenant sur choisir_carte. Une fenêtre de diagnostic concernant choisir_carte(Joueuse &j) s’affiche :

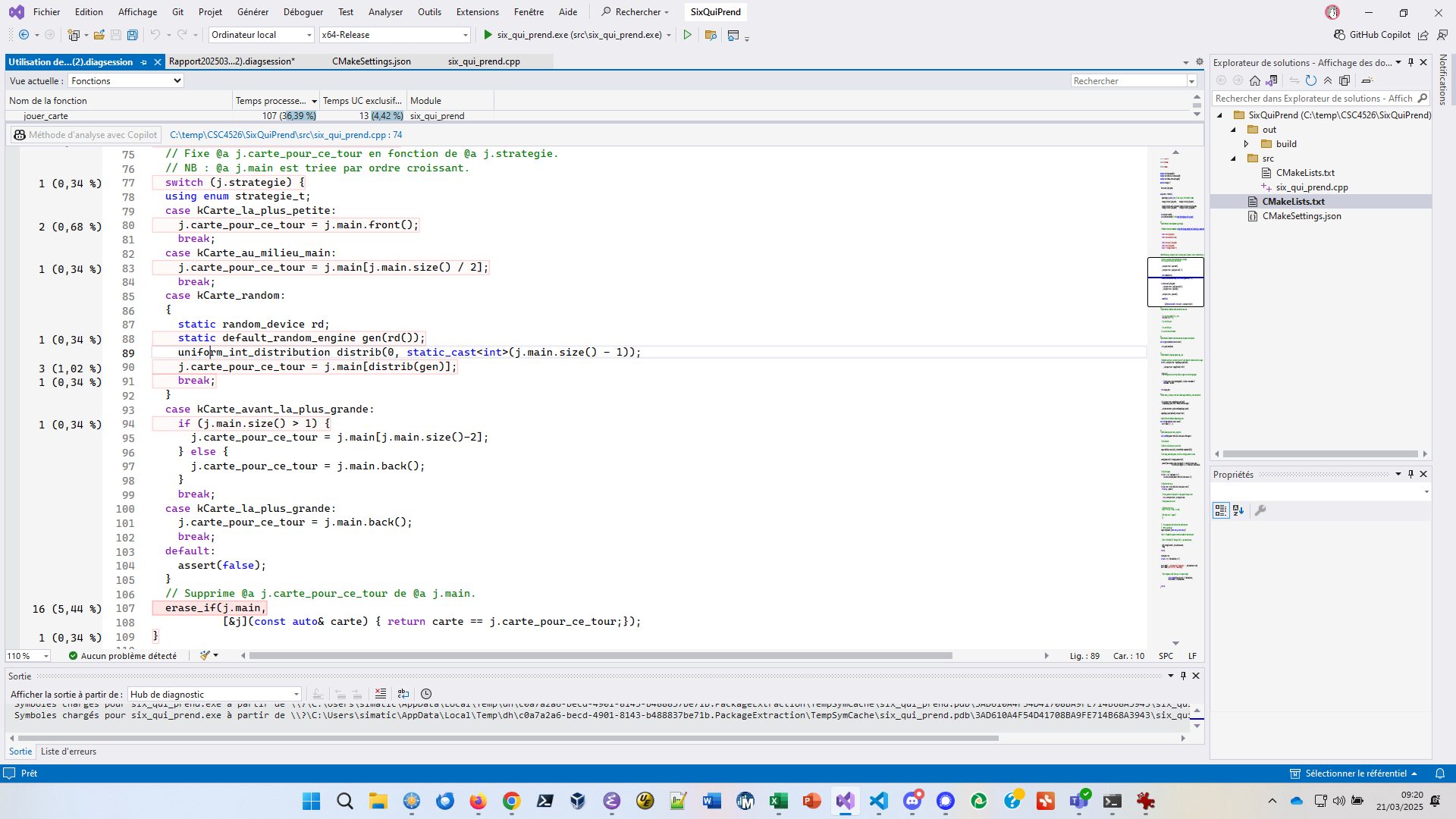
Que proposez-vous pour réduire les différents pourcentages ?

void choisir_carte(Joueuse& j) {
  // Fixe @a j.carte_pour_ce_tour en fonction de @a j.strategie.
  // NB : @a j.main est triee par ordre croissant.
  size_t index{0};
  switch (j.strategie) {
  using enum strategie_t;
  case kCarte_la_plus_petite:
    index = 0;
    break;
  case kCarte_au_milieu_main:
    index = j.main.size() / 2;
    break;
  case kCarte_random:
  {
    static random_device rd;
    static default_random_engine gen(rd());
    uniform_int_distribution distrib(0, static_cast<int>(j.main.size() - 1));
    index = distrib(gen);
    break;
  }
  case kCarte_avant_la_plus_grande:
    index = j.main.size() - (j.main.size() > 1 ? 2 : 1);
    break;
  case kCarte_la_plus_grande:
    index = j.main.size() - 1;
    break;
  default:
    assert(false);
  }
  j.carte_pour_ce_tour = j.main[index];
  // Supprime @a j.carte_pour_ce_tour de @a j.main.
  j.main.erase(j.main.begin() + index);
}

Fort de ces modifications de code, faisons un nouveau profiling pour voir le résultat de nos optimisations :

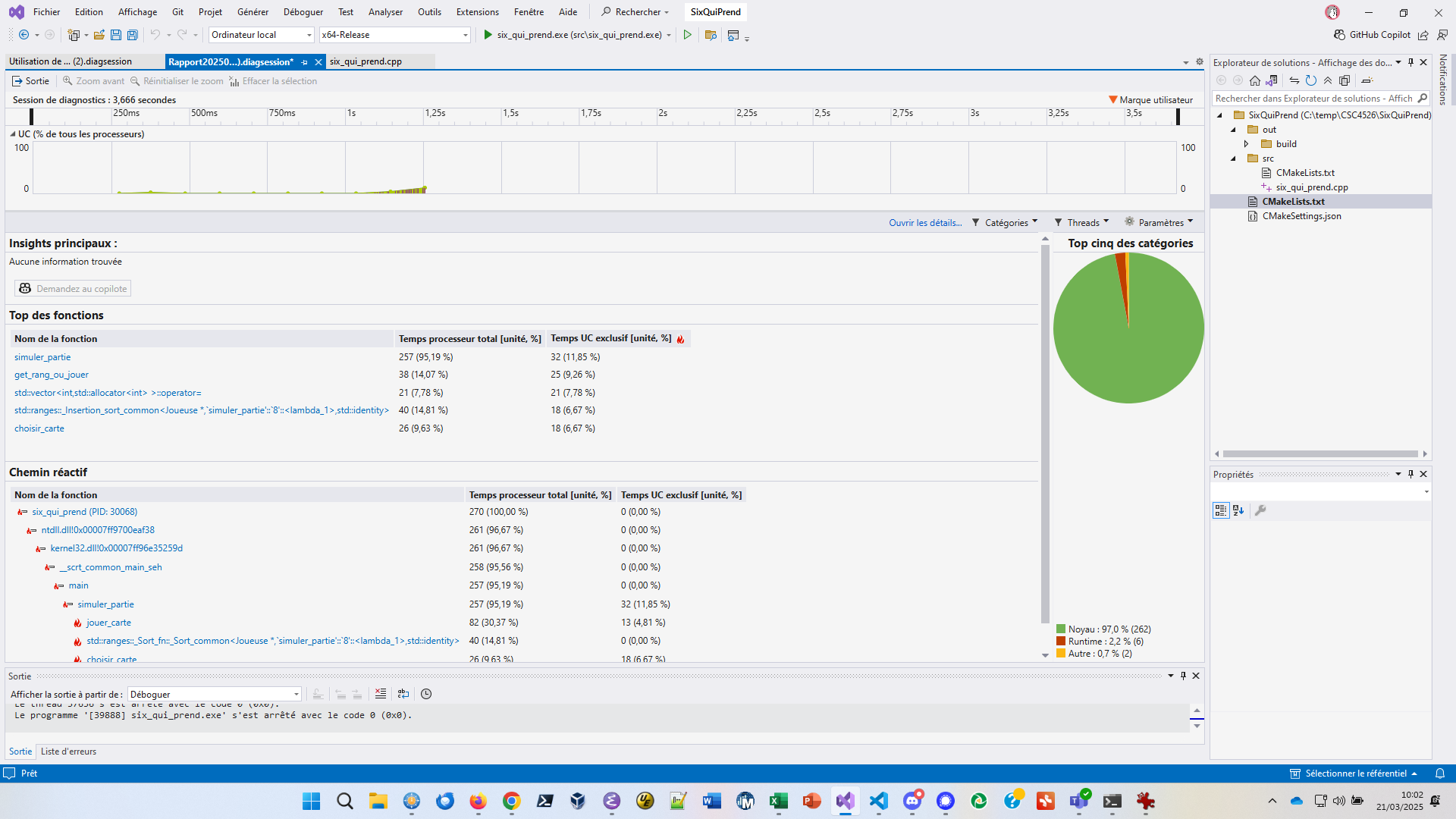
Ce nouveau rapport montre que get_rang_ou_jouer représente exclusivement 9,26%.

Cliquez sur get_rang_ou_jouer. Une fenêtre de diagnostic concernant get_rang_ou_jouer(const Joueuse &j, rangees_t &rangees) s’affiche :

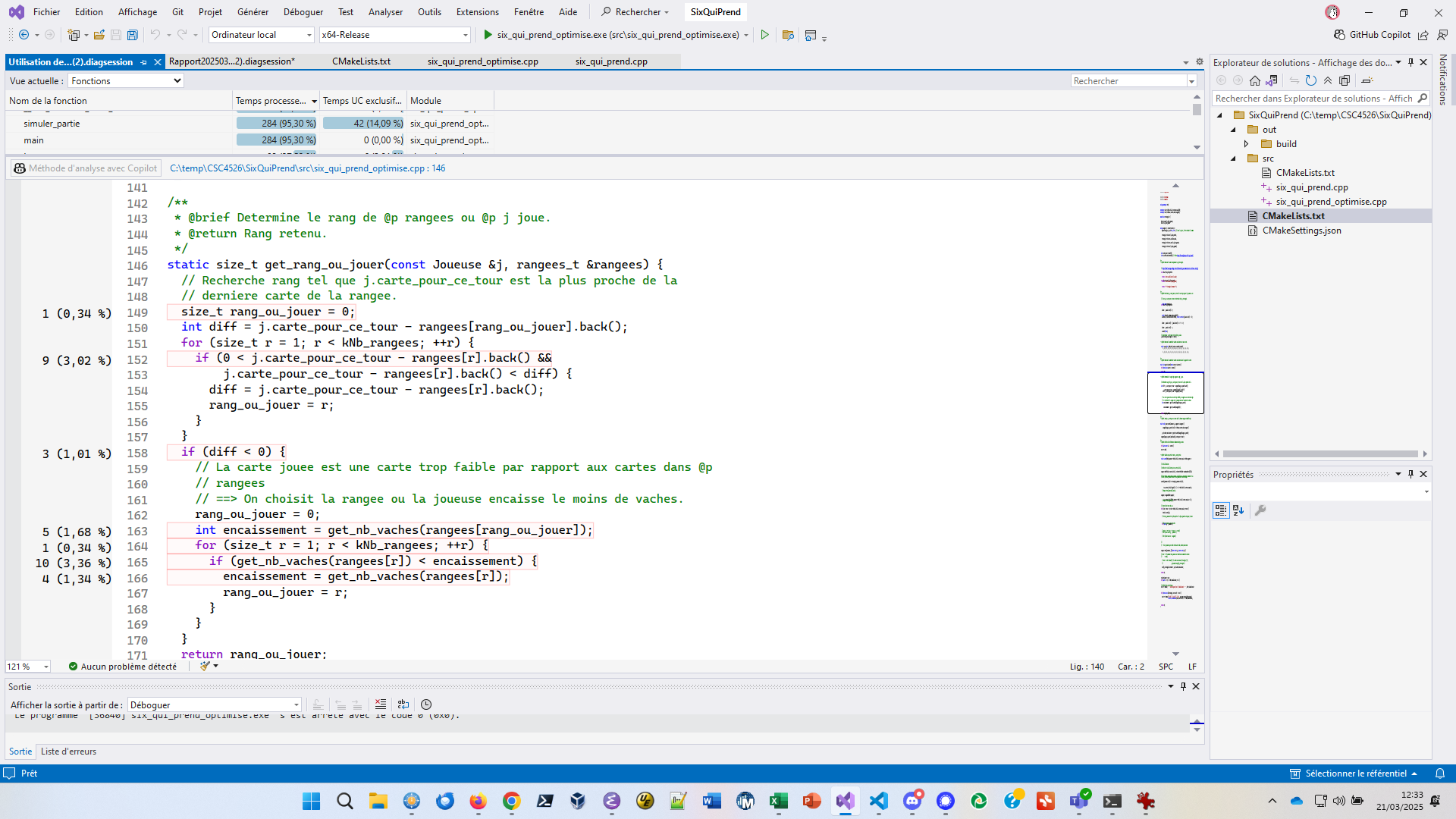
Il permet de constater que :

1. Le test if (0 < j.carte_pour_ce_tour - rangees[r].back() && j.carte_pour_ce_tour - rangees[r].back() < diff) { consomme 5,56% de CPU.
2. Le test if (get_nb_vaches(rangees[r]) < encaissement) { et la ligne encaissement = get_nb_vaches(rangees[r]); consomme 3,36% + 1,34 = 4,50% de CPU.

Que proposez-vous ?

//
// Fichier src/code/simulateur.h
//

#ifndef SIMULATEUR_OPTIMISE
using rangees_t = std::vector<cartes_t>;
#else // SIMULATEUR_OPTIMISE
using rangees_t = std::vector<std::pair<cartes_t,int>>; // first correspond aux cartes de la rangee,
                                                        // second correspond aux vaches encaissable dans cette rangee.
#endif// SIMULATEUR_OPTIMISE

//
// Fichier src/code/simulateur_optimise.cpp
//

#define SIMULATEUR_OPTIMISE // Ce #define est ajoute **avant** le #include "simulateur.h" pour influencer les lignes incluses.
#include "simulateur.h"

size_t get_rang_ou_jouer(const Joueuse &j, rangees_t &rangees) {
  // Recherche rang tel que j.carte_pour_ce_tour est la plus proche de la
  // derniere carte de la rangee.
  size_t rang_ou_jouer = 0;
  int diff = j.carte_pour_ce_tour - rangees[rang_ou_jouer].first.back();
  for (size_t r = 1; r < kNb_rangees; ++r) {
    if (auto diff_r = j.carte_pour_ce_tour - rangees[r].first.back();
        0 < diff_r && diff_r < diff) {
      diff = diff_r;
      rang_ou_jouer = r;
    }
  }
  if (diff < 0) {
    // La carte jouee est une carte trop faible par rapport aux cartes dans @p
    // rangees
    // ==> On choisit la rangee ou la joueuse encaisse le moins de vaches.
    rang_ou_jouer = 0;
    for (size_t r = 1; r < kNb_rangees; ++r) {
      if (rangees[r].second < rangees[rang_ou_jouer].second) {
        rang_ou_jouer = r;
      }
    }
  }
  return rang_ou_jouer;
}

//
// // jouer_carte() est modifiee
//
void jouer_carte(Joueuse &j, rangees_t &rangees) {
  size_t rang_ou_jouer{get_rang_ou_jouer(j, rangees)};
  if (j.carte_pour_ce_tour < rangees[rang_ou_jouer].first.back() ||
      rangees[rang_ou_jouer].first.size() >= kNb_max_cartes_dans_rangee) {
    j.cartes_encaissees.insert(j.cartes_encaissees.end(),
                               rangees[rang_ou_jouer].first.begin(),
                               rangees[rang_ou_jouer].first.end());
    j.nb_vaches_encaissees += rangees[rang_ou_jouer].second;
    rangees[rang_ou_jouer].first.clear();
    rangees[rang_ou_jouer].second = 0;
  }
  rangees[rang_ou_jouer].first.push_back(j.carte_pour_ce_tour);
  rangees[rang_ou_jouer].second += get_nb_vaches(j.carte_pour_ce_tour);
}

//
// L'initialisation de rangees est modifiee
//
  for (size_t i = 0; i < kNb_rangees; ++i) {
    rangees[i].first.push_back(
        tas_cartes_initial[kNb_joueuses * kNb_initial_cartes_en_main + i]);
    rangees[i].second = get_nb_vaches(rangees[i].first.front());
    // dump_cartes(rangees[i]);
  }

//
// Fichier src/code/unitTests.cpp
//

#define SIMULATEUR_OPTIMISE // Ce #define est ajoute **avant** le #include "simulateur.h" pour influencer les lignes incluses.
#include "simulateur.h"

TEST(get_rang_ou_jouer, la_carte_peut_etre_ajoutee_a_une_rangee) {
  const Joueuse j{
    strategie_t::kCarte_la_plus_grande,
    {2, 4, 6},
    42,
    {},
    0
  };
#ifndef SIMULATEUR_OPTIMISE
  const rangees_t rangees{
    {6, 7, 8},
    {38, 39, 40},
    {50, 60},
    {103, 104}
  };
#else // SIMULATEUR_OPTIMISE
  const rangees_t rangees{
      {{6, 7, 8}, 3},
      {{38, 39, 40}, 5},
      {{50, 60}, 6},
      {{103, 104}, 2}
  };
#endif // SIMULATEUR_OPTIMISE

  EXPECT_EQ(1, get_rang_ou_jouer(j, rangees));
}

TEST(get_rang_ou_jouer, la_carte_est_trop_petite_et_doit_se_substituer_a_la_rangee_qui_rapporte_le_moins_de_vaches) {
  const Joueuse j{
    strategie_t::kCarte_la_plus_grande,
    {2, 4, 6},
    42,
    {},
    0
  };
#ifndef SIMULATEUR_OPTIMISE
  const rangees_t rangees{
      {6, 7, 8, 98}, // Nombre de vaches = 4
      {38, 39, 90},  // Nombre de vaches = 5
      {50, 60}, // Nombre de vaches = 6
      {103, 104} // Nombre de vaches = 2
  };
#else // SIMULATEUR_OPTIMISE
  const rangees_t rangees{
        {{6, 7, 8, 98}, 4}, // Nombre de vaches = 4
        {{38, 39, 90}, 5}, // Nombre de vaches = 5
        {{50, 60}, 6},// Nombre de vaches = 6
        {{103, 104}, 2} // Nombre de vaches = 2
  };
#endif // SIMULATEUR_OPTIMISE

  EXPECT_EQ(3, get_rang_ou_jouer(j, rangees));
}

TEST(jouer_carte, la_carte_est_ajoutee_a_une_rangee_de_moins_de_5_cartes) {
  const Joueuse j_init{
    strategie_t::kCarte_la_plus_grande,
    {2, 4, 6},
    42,
    {12, 13},
    2
  };
  Joueuse j{j_init};
#ifndef SIMULATEUR_OPTIMISE
  const rangees_t rangees_init{
      {6, 7, 8},
      {38, 39, 40},
      {50, 60},
      {103, 104}
  };
#else // SIMULATEUR_OPTIMISE
  const rangees_t rangees_init{
        {{6, 7, 8}, 3},
        {{38, 39, 40}, 5},
        {{50, 60}, 6},
        {{103, 104}, 2}
  };
#endif // SIMULATEUR_OPTIMISE
  rangees_t rangees{rangees_init};

  jouer_carte(j, rangees);

  EXPECT_EQ(j_init.main, j.main);
  EXPECT_EQ(j_init.cartes_encaissees, j.cartes_encaissees);
  EXPECT_EQ(j_init.nb_vaches_encaissees, j.nb_vaches_encaissees);
  EXPECT_EQ(rangees_init[0], rangees[0]);
#ifndef SIMULATEUR_OPTIMISE
  EXPECT_EQ(cartes_t({38, 39, 40, 42}), rangees[1]);
#else // SIMULATEUR_OPTIMISE
  EXPECT_EQ(make_pair(cartes_t({38, 39, 40, 42}), 6), rangees[1]);
#endif // SIMULATEUR_OPTIMISE
  EXPECT_EQ(rangees_init[2], rangees[2]);
  EXPECT_EQ(rangees_init[3], rangees[3]);
}

  TEST(jouer_carte, la_carte_est_ajoutee_a_une_rangee_de_5_cartes) {
  const Joueuse j_init{
    strategie_t::kCarte_la_plus_grande,
    {2, 4, 6},
    42,
    {12, 13},
    2
  };
  Joueuse j{j_init};
#ifndef SIMULATEUR_OPTIMISE
  const rangees_t rangees_init{
          {6, 7, 8},
          {35, 36, 38, 39, 40},
          {50, 60},
          {103, 104}
  };
#else // SIMULATEUR_OPTIMISE
  const rangees_t rangees_init{
            {{6, 7, 8}, 3},
            {{35, 36, 38, 39, 40}, 8},
            {{50, 60}, 6},
            {{103, 104}, 2}
  };
#endif // SIMULATEUR_OPTIMISE
  rangees_t rangees{rangees_init};

  jouer_carte(j, rangees);

  EXPECT_EQ(j_init.main, j.main);
  EXPECT_EQ(cartes_t({12, 13, 35, 36, 38, 39, 40}), j.cartes_encaissees);
  EXPECT_EQ(10, j.nb_vaches_encaissees);
  EXPECT_EQ(rangees_init[0], rangees[0]);
#ifndef SIMULATEUR_OPTIMISE
  EXPECT_EQ(cartes_t({42}), rangees[1]);
#else // SIMULATEUR_OPTIMISE
  EXPECT_EQ(make_pair(cartes_t({42}), 1), rangees[1]);
#endif // SIMULATEUR_OPTIMISE
  EXPECT_EQ(rangees_init[2], rangees[2]);
  EXPECT_EQ(rangees_init[3], rangees[3]);
}

  TEST(jouer_carte, la_carte_se_substitue_a_une_rangee_de_cartes) {
  const Joueuse j_init{
    strategie_t::kCarte_la_plus_grande,
    {2, 4, 6},
    42,
    {12, 13},
    2
  };
  Joueuse j{j_init};
#ifndef SIMULATEUR_OPTIMISE
  const rangees_t rangees_init{
        {6, 7, 8, 98}, // Nombre de vaches = 4
        {38, 39, 90},  // Nombre de vaches = 5
        {50, 60}, // Nombre de vaches = 6
        {103, 104} // Nombre de vaches = 2
  };
#else // SIMULATEUR_OPTIMISE
  const rangees_t rangees_init{
          {{6, 7, 8, 98}, 4},// Nombre de vaches = 4
          {{38, 39, 90}, 5}, // Nombre de vaches = 5
          {{50, 60}, 6}, // Nombre de vaches = 6
          {{103, 104}, 2} // Nombre de vaches = 2
  };
#endif // SIMULATEUR_OPTIMISE
  rangees_t rangees{rangees_init};

  jouer_carte(j, rangees);

  EXPECT_EQ(j_init.main, j.main);
  EXPECT_EQ(cartes_t({12, 13, 103, 104}), j.cartes_encaissees);
  EXPECT_EQ(4, j.nb_vaches_encaissees);
  EXPECT_EQ(rangees_init[0], rangees[0]);
  EXPECT_EQ(rangees_init[1], rangees[1]);
  EXPECT_EQ(rangees_init[2], rangees[2]);
#ifndef SIMULATEUR_OPTIMISE
  EXPECT_EQ(cartes_t({42}), rangees[3]);
#else // SIMULATEUR_OPTIMISE
  EXPECT_EQ(std::make_pair(cartes_t({42}), 1), rangees[3]);
#endif // SIMULATEUR_OPTIMISE
}

Fort de ces nouvelles modifications de code, faisons un nouveau profiling pour voir le résultat de nos optimisations :

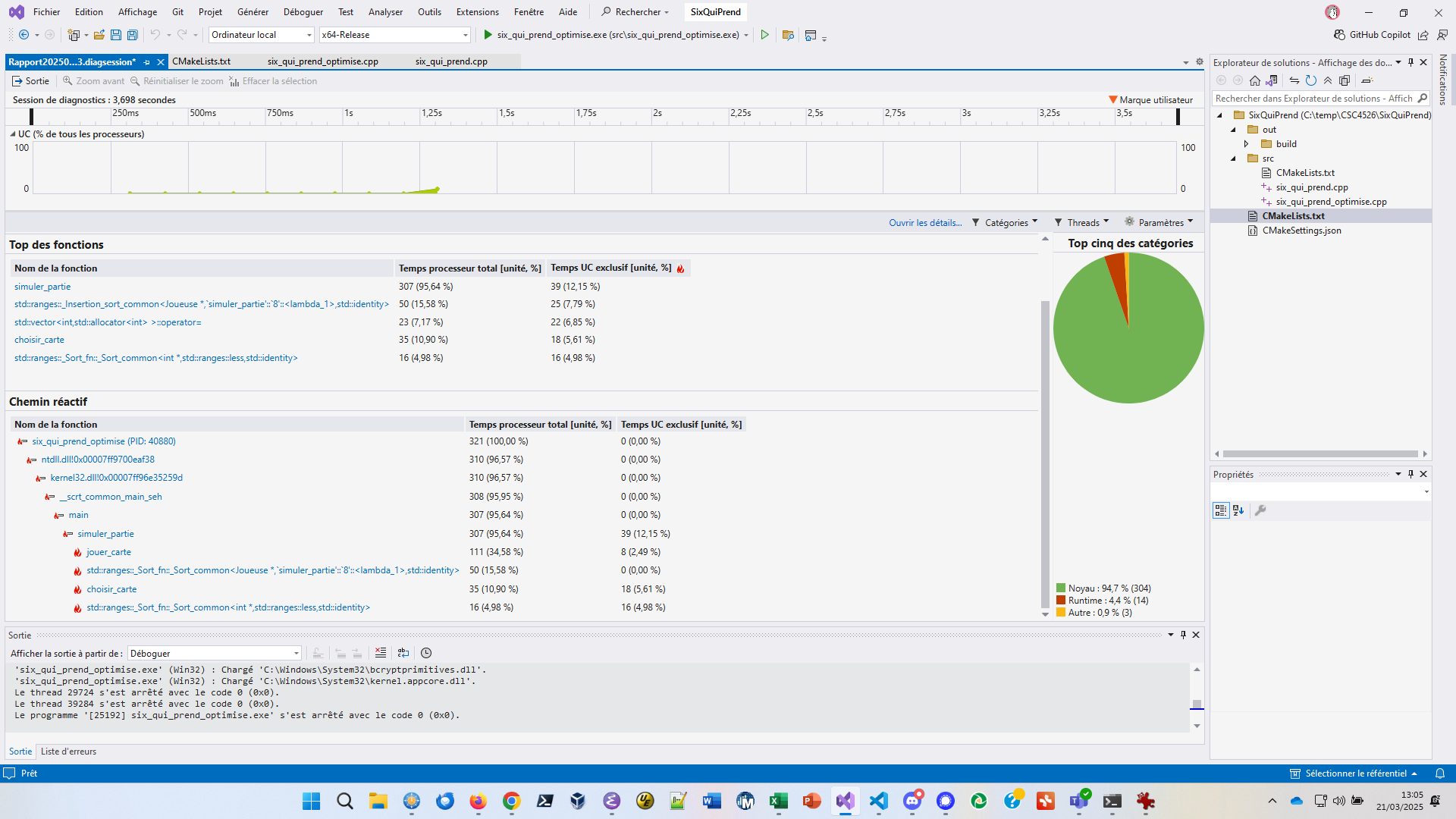
Ce nouveau rapport montre que les get_rang_ou_jouer représente exclusivement 9,26%.

La sous-fenêtre “Chemin réactif” montre que le temps passé dans simuler_partie est lié au temps passé dans jouer_carte et dans std::ranges::_Sort_fn :

Cliquer sur jouer_carte montre qu’on ne peut plus vraiment améliorer ce code :

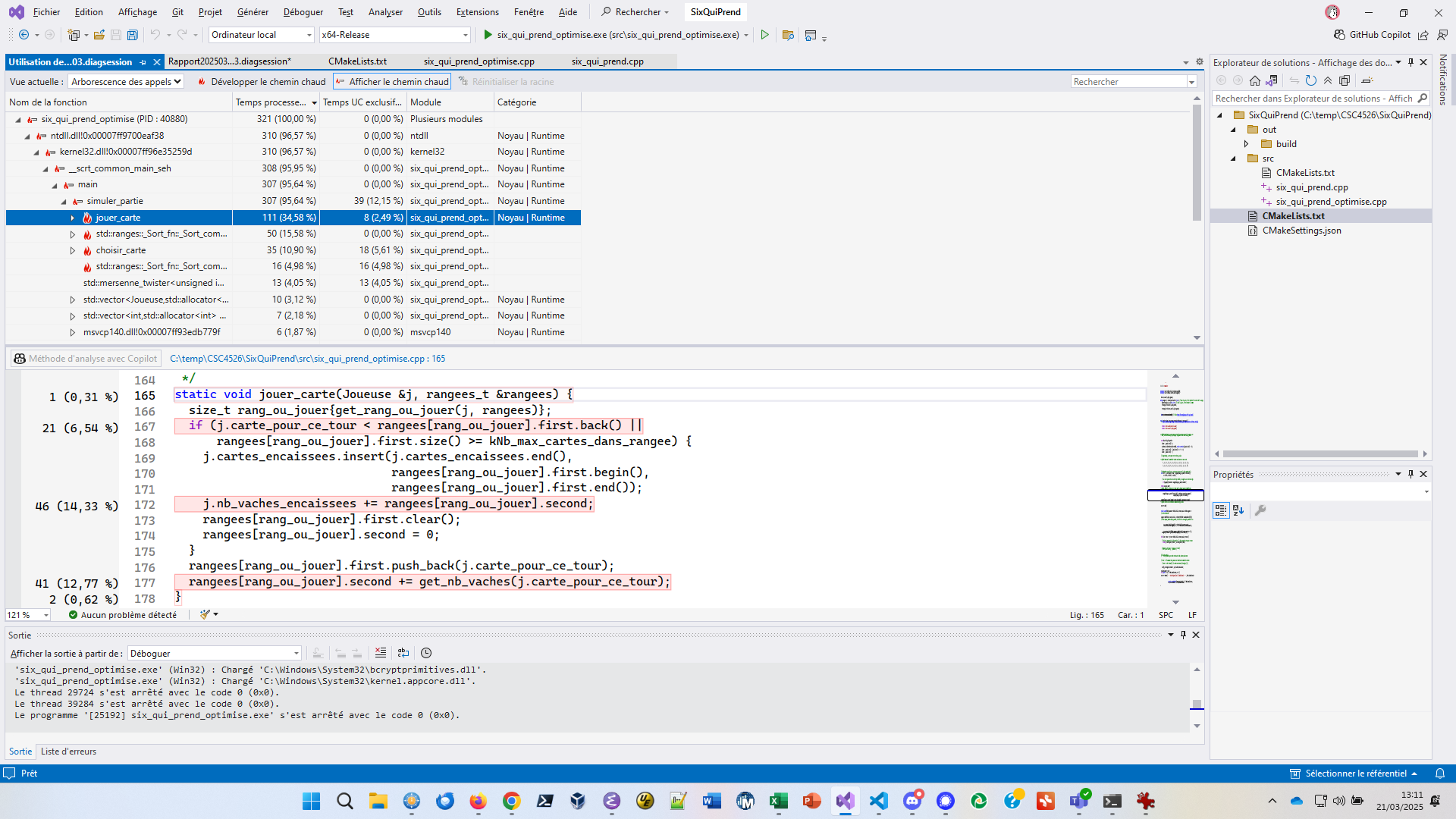
En revanche, pour std::ranges::_Sort_fn, en cliquant sur son diagnostic :

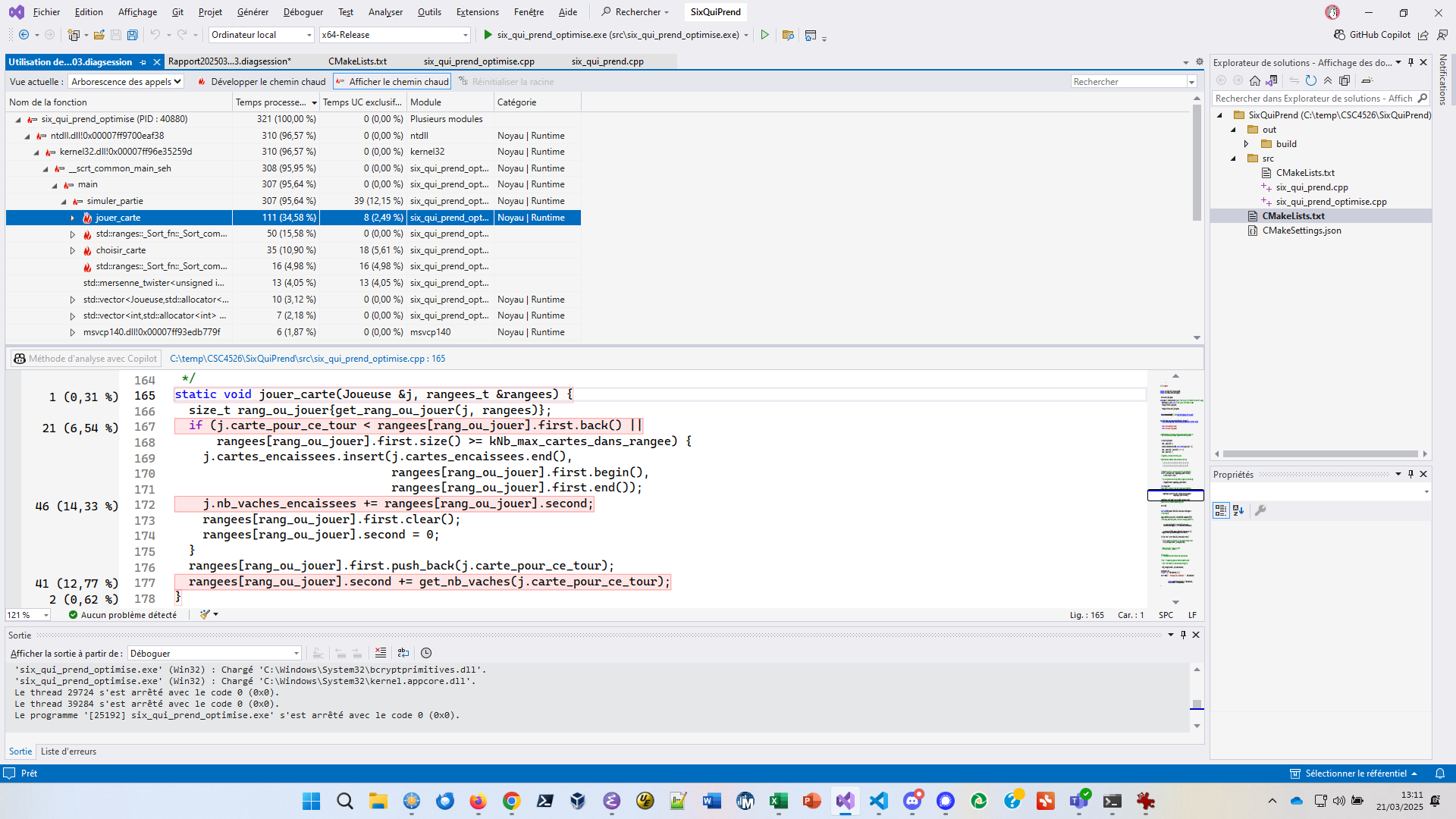
on constate que le tri qui consomme de la CPU est un tri. Cliquez droit sur ce tri et demandez l’affichage du “Flame graph” :

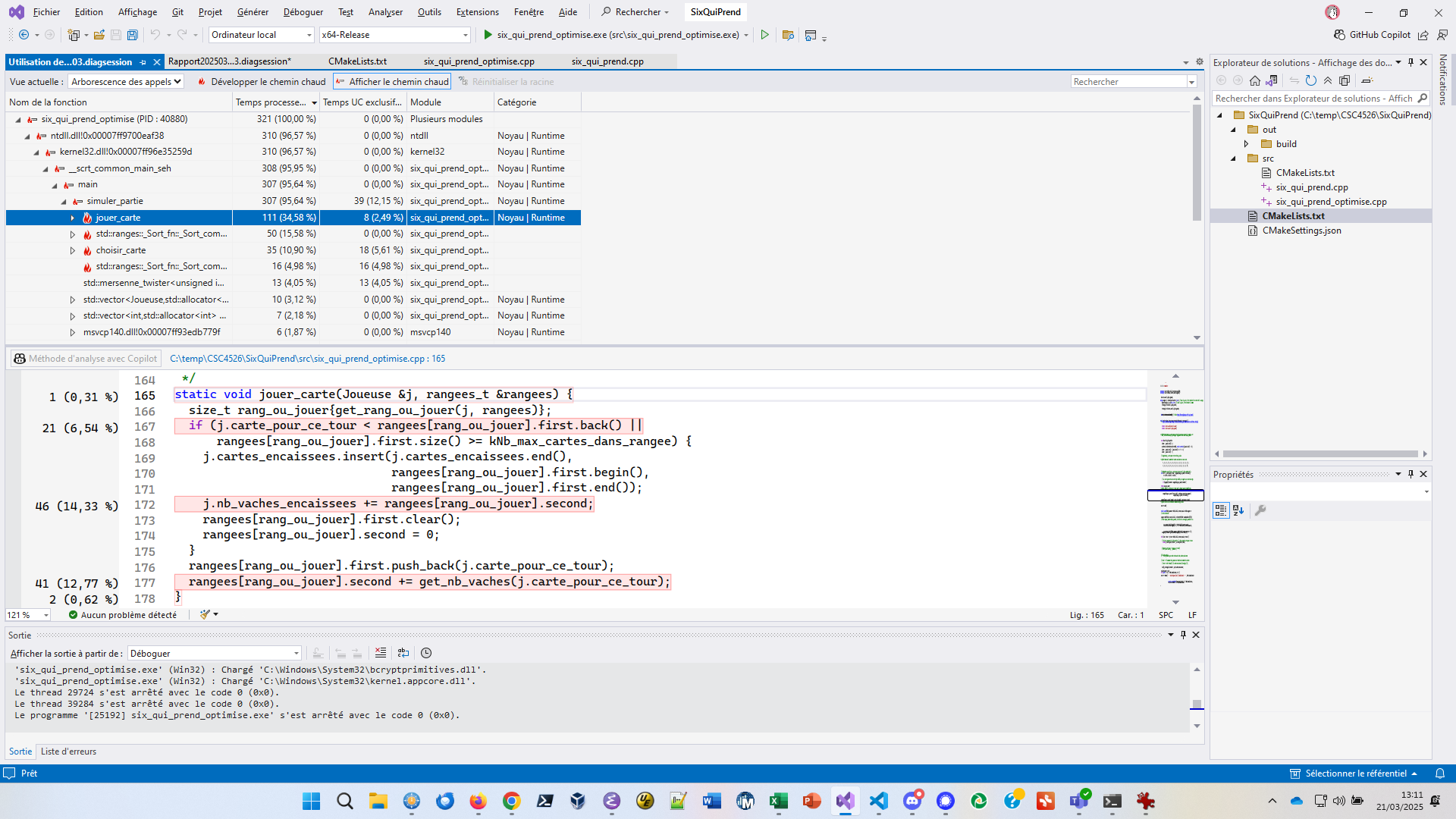
Le tri qui pose souci est celui de joueuses. En effet, pour trier joueuses, nous avons besoin de faire des permutations de Joueuse_t, ce qui est coûteux en CPU et en mémoire. Il serait plus efficace de trier un tableau d’index sur joueuses.

  // Initialisation d'un vecteur contenant des index dans @a joueuses. C'est ce
  // vecteur qu'on trie pour obtenir @a joueuses trie sans utiliser
  // ranges::sort(joueuses...)
  vector<size_t>index_pour_joueuses_triees(kNb_joueuses);
  iota(index_pour_joueuses_triees.begin(), index_pour_joueuses_triees.end(), 0);

  //
  // Simulation des tours de jeu.
  //
  for (size_t tour = 1; tour <= kNb_initial_cartes_en_main; ++tour) {
    // Chaque joueuse choisit sa carte.
    for (auto &j : joueuses) {
      choisir_carte(j);
    }

    // Trie @a index_pour_joueuses_triees pour connaitre @a joueuses trie
    // de la plus petite à la plus grande carte_pour_ce_tour.
    ranges::sort(index_pour_joueuses_triees, [&joueuses](const auto &i1, const auto &i2) {
      return joueuses[i1].carte_pour_ce_tour < joueuses[i2].carte_pour_ce_tour;
    });

    // Chaque joueuse joue sa carte.
    for (const auto &i : index_pour_joueuses_triees) {
      jouer_carte(joueuses[index_pour_joueuses_triees[i]], rangees);
    }

    [...]
  }

Par ailleurs, pour le mélange, peut-être aviez-vous la ligne ranges::shuffle(tas_cartes_initial, std::mt19937{std::random_device{}()});. Si c’est le cas, remplacez-la par les lignes :

  static random_device rd;
  static mt19937 gen(rd());
  ranges::shuffle(tas_cartes_initial, gen);

Au final, après ces différentes optimisations, pour 100.000 simulations compilées en mode Release :

• Measure-Command { .\main.exe | Out-Default } (/usr/bin/time ./.\main.exe sous Linux, time ./.\six_qui_prend.exe sous macOS) affiche un temps d’exécution de 2700 millisecondes.
• Measure-Command { .\main_optimise.exe | Out-Default } affiche un temps d’exécution de 1800 millisecondes, soit une réduction de 33% du temps d’exécution .

Corrigé (à exploiter selon la procédure cmake de ce document).