Langage C : Tableaux et structures
L'objectif de cette session d'exercices est de manipuler des tableaux et des structures.
Le triangle de Sierpiński (~ 3h)
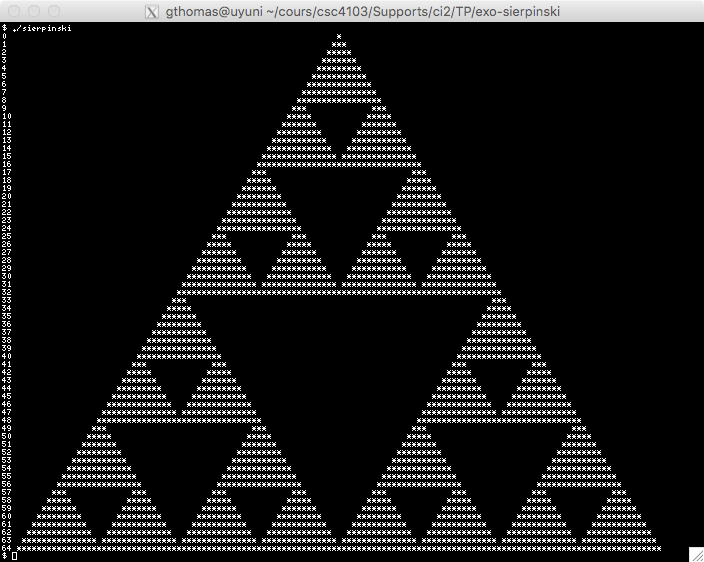
Le but de cet exercice est de créer une approximation du triangle de Sierpiński. La figure ci-dessous vous présente
cette approximation.
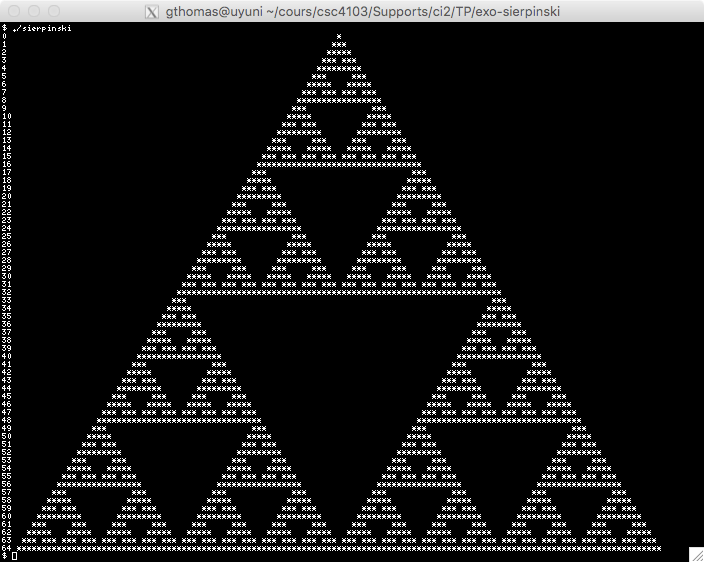 Ce triangle est une fractale.
On peut l'obtenir en appliquant l'algorithme illustré dans la figure ci-dessous.
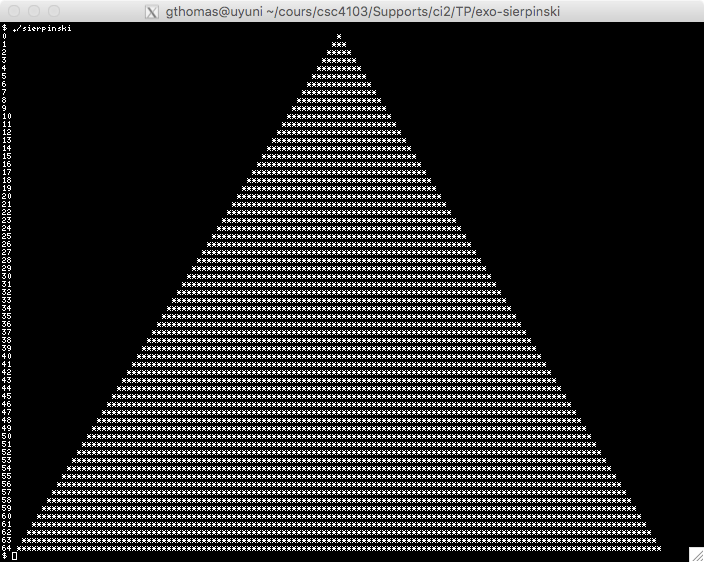
À l'étape 0, on commence par dessiner un triangle.
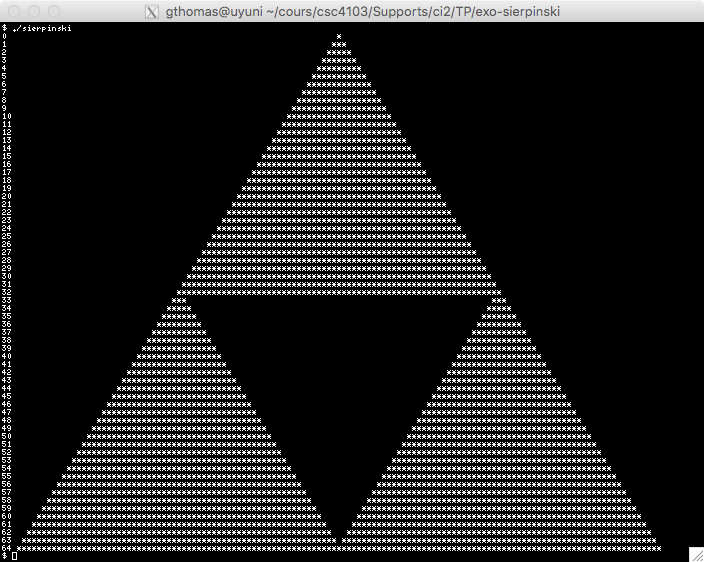
Ensuite, à l'étape 1, on supprime le triangle central, ce qui laisse donc 3 triangles.
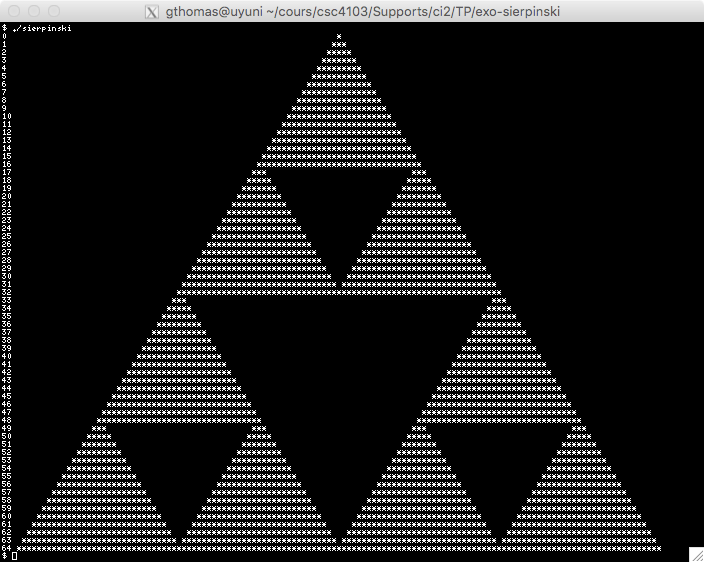
À l'étape 2, on recommence le procédé sur les trois triangles, ce qui construit donc 9 triangles.
Pour passer de l'étape n à l'étape n + 1, on applique le même algorithme :
on supprime les triangles centraux des 3n triangles de l'étape n.
Le triangle de Sierpiński est défini comme étant la figure résultant de l'application de cet algorithme
une infinité de fois.
Ce triangle est une fractale.
On peut l'obtenir en appliquant l'algorithme illustré dans la figure ci-dessous.
À l'étape 0, on commence par dessiner un triangle.
Ensuite, à l'étape 1, on supprime le triangle central, ce qui laisse donc 3 triangles.
À l'étape 2, on recommence le procédé sur les trois triangles, ce qui construit donc 9 triangles.
Pour passer de l'étape n à l'étape n + 1, on applique le même algorithme :
on supprime les triangles centraux des 3n triangles de l'étape n.
Le triangle de Sierpiński est défini comme étant la figure résultant de l'application de cet algorithme
une infinité de fois.
Dans l'exercice, nous construisons l'approximation à l'étape n du triangle.
Pour cela, nous appliquons un algorithme légèrement différent, consistant à dessiner directement
les 3n triangles.
L'exercice est divisé en 5 étapes. Faire les trois premières est obligatoire.
Il faut aussi que vous commenciez la quatrième étape, mais il n'est pas forcément réaliste
que tous les étudiants puissent la finir dans le temps imparti.
Enfin, la cinquième étape, relativement rapide, ne vous fera pas assimiler de nouvelle
notion. Cette étape n'est donc pas obligatoire, mais elle permet de voir ce triangle
apparaître, ce qui est relativement satisfaisant.
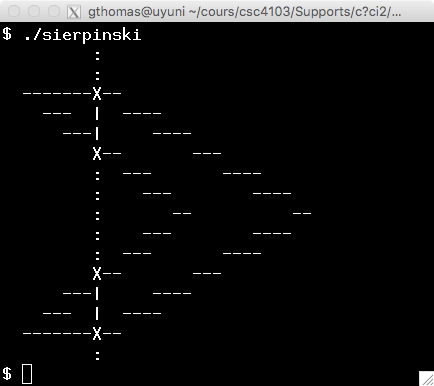
Pour effectuer le remplissage du polygone, nous balayons la figure en suivant l'axe des abscisses.
La figure b représente le balayage de l'axe 9.
Lorsqu'on balaye un axe, on commence par identifier toutes les intersections
entre l'axe balayé et les côtés du polygone.
Sur notre figure, en balayant l'axe 9, on obtient les points
(9, 1), (9, 3.625), (9, 10.375) et (9, 13) représentés par le symbole X
sur la figure.
En triant ces points suivant l'axe y, on observe que cette suite donne exactement
les lignes verticales à tracer si on prend les points 2 à 2 :
dans notre cas, il suffit de tracer les lignes (9, 1) à (9, 3.625) et
(9, 10.325) à (9, 13).

|
|
|
|
| Étape 0 | Étape 1 | Étape 2 | Étape 3 |
Je trie, tu tries (∼ 40mn, obligatoire)
Pour construire le triangle de Sierpiński, nous aurons besoin de trier un tableau de nombres
flottants.
Dans cette première partie, nous mettons donc en œuvre l'algorithme de tri.
Nous utilisons l'algorithme de tri par insertion.
Cet algorithme n'est pas très efficace pour trier des grandes séquences, mais
s'avère être particulièrement efficace sur de petites séquences.
Le principe de l'algorithme est illustré dans la figure ci-dessous.
Pour commencer, avec l'algorithme de tri par insertion, on s'assure qu'un tableau est toujours
trié.
Pour insérer un élément n, on parcourt le tableau (étape b) en cherchant
l'emplacement de n (étape c).
Une fois cet emplacement i trouvé, on déplace d'une case à droite tous les éléments
du tableau se trouvant à droite de la case i (étape d).
Enfin, on insère le nombre n dans la case i (étape e).
+-----------------------+
| 1 | 3 | 5 | 7 | | |
+-----------------------+
|
+-----------------------+
| 1 | 3 | 5 | 7 | | |
+-----------------------+
↑ |
+-----------------------+
| 1 | 3 | 5 | 7 | | |
+-----------------------+
↑ |
| a. Tableau de départ | b. Cherche emplacement pour 4 | c. Trouve emplacement pour 4 |
+-----------------------+
| 1 | 3 | 5 | 5 | 7 | |
+-----------------------+
↑ |
+-----------------------+
| 1 | 3 | 4 | 5 | 7 | |
+-----------------------+
↑ |
| d. Déplace d'un cran à droite | e. Insère 4 |
Pour commencer, dans une votre fonction main, déclarez
un tableau nommé tab de nombres flottants de 5 cases initialisé aux valeurs 1, 3, 5, 7, 0.
Ensuite, affichez les 5 cases du tableau à l'aide d'une boucle.
Nous mettons maintenant en œuvre la fonction de recherche.
Écrivez une fonction sort_get_index prenant en argument :
- un tableau de flottants nommé tab,
- l'indice maximal actuel du tableau top,
- un nombre flottant à insérer val.
- L'indice, compris entre 0 et top-1, contenant la première valeur supérieure à val si elle existe,
- L'indice top sinon.
$ ./sierpinski
Insert 0 at 0, 3.5 at 2, 10 at 4
1.000000 3.000000 5.000000 7.000000 0.000000
Conservez le code d'affichage du tableau qui vous servira aux prochaines questions.
Nous mettons maintenant en œuvre la fonction de déplacement à droite et d'insertion.
Écrivez une fonction sort_insert_at prenant en argument :
- un tableau de flottants nommé tab,
- l'indice d'insertion i,
- l'indice maximal actuel du tableau top,
- le nombre flottant à insérer val.
$ ./sierpinski
Insert 0 at 0, 3.5 at 2, 10 at 4
1.000000 3.000000 3.500000 5.000000 7.000000
Nous pouvons maintenant écrire la fonction d'insertion.
Écrivez une fonction nommée sort_insert prenant les mêmes arguments
que sort_get_index. Cette fonction doit utiliser
sort_get_index et sort_insert_at pour insérer
le nouvel élément.
Testez votre fonction en remplaçant le test de sort_insert_at
par l'insertion de l'élément 2.
Des grilles et des points (∼ 30mn, obligatoire)
Dans cette partie, nous créons une grille finie.
Nous représentons une grille de n colonnes par m lignes
avec un tableau de caractères de taille n * m.
Les n premiers éléments contiennent la première ligne, les n
suivants la seconde, etc.
De façon à modifier facilement la taille de notre grille ultérieurement, nous définissons
deux fonctions nommées
int nb_columns() et int nb_lines() qui renvoient respectivement
les valeurs 32 et 16.
Après avoir supprimé le code testant les fonctions de tri de la fonction main,
affichez les dimensions de la grille dans la fonction main
de façon à vérifier que vos fonctions sont correctes.
Dans la fonction main, supprimez l'affichage, et créez à la place
un tableau nommé grid de nb_lines() * nb_columns() caractères.
Affectez le premier élément de la grille à la valeur * et affichez
ce caractère.
Maintenant que la grille est en place, nous pouvons l'initialiser.
Écrivez une fonction grid_init prenant en argument :
(i) un tableau de caractères grid et (ii) un caractère pixel.
Cette fonction doit initialiser les nb_lines() * nb_columns() cases du tableau grid à la
valeur pixel.
Dans la fonction main, remplacez l'initialisation du premier caractère à la valeur
* par une initialisation de la grille complète avec le caractère *.
Conservez l'affichage du premier élément de la grille de façon à vérifier que votre programme
est correct.
Le but de cette question est d'écrire une fonction affichant la grille.
Écrivez une fonction grid_display prenant en paramètre
un tableau de caractères grid.
Cette fonction doit afficher, sur chaque ligne du terminal, une ligne de la grille.
Dans la fonction main, remplacez l'affichage du premier élément de la grille
par l'affichage de toute la grille.
Écrivez une fonction nommée plot_point prenant en paramètre :
(i) une grille grid, (ii) une coordonnée entière x,
(iii) une coordonnée entière y et (iv) un caractère pixel.
Cette fonction doit placer le caractère pixel en (x, y) dans la grille.
De façon à éviter une gymnastique intellectuelle infernale, nous considérons
que le point en bas à gauche de la grille correspond au point de coordonnées
(0, 0). Pour cette raison, placer le caractère pixel
de coordonnées (x, y) revient à mettre le caractère pixel
à l'intersection entre la ligne nb_lines() - y - 1 et la colonne x.
Pour tester votre programme, dans la fonction main,
placez le caractère espace (' ') en (3, 1), et
vérifiez soigneusement que votre repère est bien orienté dans le sens direct.
Vous devriez obtenir l'affichage suivant:
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
********************************
*** ****************************
********************************
De façon à vous prémunir contre les bugs que vous allez peut-être rencontrer,
modifiez votre fonction plot_point de façon à afficher
un message d'erreur et à quitter si x ou y
tombent en dehors de la grille.
Vérifiez que votre code est correct en essayant d'afficher le point
de coordonnées (3, 100).
Pour quitter un programme C, il faut ajouter la ligne #include <stdlib.h>
au début du fichier et appeler la fonction exit(EXIT_FAILURE) à l'endroit
où vous souhaitez quitter.
Des lignes verticales (∼ 20mn, obligatoire)
Pour pouvoir dessiner le triangle de Sierpiński, il faut être capable de dessiner des
polygones pleins.
Et pour dessiner des polygones pleins, nous aurons besoin de dessiner des lignes
verticales.
Dessiner une ligne verticale ne représente pas de difficulté majeure, mais le problème
se complique légèrement car les coordonnées des polygones vont être représentées
par des nombres flottants.
Il faut donc être capable de projeter une ligne verticale représentée par des coordonnées
flottantes sur une grille utilisant des coordonnées entières.
Écrivez une fonction plot_vline prenant
en paramètre :
- un tableau de caractères grid,
- une abscisse entière x,
- une ordonnée flottante fy0,
- une ordonnée flottante fy1,
- un caractère pixel.
Nous nous occupons maintenant de convertir correctement les flottants en entiers.
Dans un premier temps, nous souhaitons arrondir le flottant vers la valeur entière
la plus proche. De cette façon, le segment [1.2, 3.8] va être
converti en [1, 4] et le segment [1.7, 3.3] en
[2,3]. Cet arrondi donne un rendu graphique relativement esthétique.
Malheureusement, la conversion d'un flottant vers un entier en C tronque simplement
la partie décimale du nombre flottant. Donc, actuellement, le nombre 3.8 est
converti en 3, ce qui n'est pas ce que nous attendons.
Toutefois, vous pouvez remarquer que si nous arrondissons un nombre flottant
f en tronquant la partie décimale de f + 0.5,
vous avez exactement l'arrondi que nous attendons : 1.2 est converti
en E(1.2 + 0.5) = 1 et 3.8 en E(3.8 + 0.5) = 4.
Modifiez votre fonction plot_vline pour effectuer cet arrondi.
Testez vos arrondis en dessinant, après la ligne (1, 2) à (1, 3), les lignes
(2, 1.7) à (2, 3.3) et (3, 1.2) à (3, 3.8).
Se pose maintenant le problème de savoir comment arrondir les nombres
ayant pour partie décimale 0.5. En effet, on pourrait projeter
le segment [0.5, 1.5] en [0, 2], [0, 1], [1, 2] ou [1, 1].
Toutes ces solutions sont bien entendu correctes, mais il est plus esthétique
de se restreindre à des projections symétriques autour de 1 :
soit [0, 2], soit [1, 1].
Avec notre algorithme actuel, le nombre 0.5 est converti en 1 et le nombre
1.5 en 2, ce qui ne convient donc pas.
Pour adopter la première solution, nous vous proposons de retirer donc 1 à y0 si
fy0 est égal y0 - 0.5, c'est à dire si la partie décimale de fy0 est égale à 0.5.
Testez votre fonction en ajoutant la ligne allant de (7, 0.5) à (7, 1.5) à votre grille.
La figure que vous devriez obtenir à cette étape est la suivante :
|
|||
||| |
| |
|
De jolis polygones (∼ 1h10, obligatoire jusqu'à la question p)
Nous pouvons maintenant commencer à dessiner les polygones qui permettront de dessiner
le triangle de Sierpiński.
La figure ci-dessous présente le principe.
Un polygone est défini par un ensemble de points appelés les coins du polygone.
Le but de cette partie est de remplir un polygone à partir de ses points.
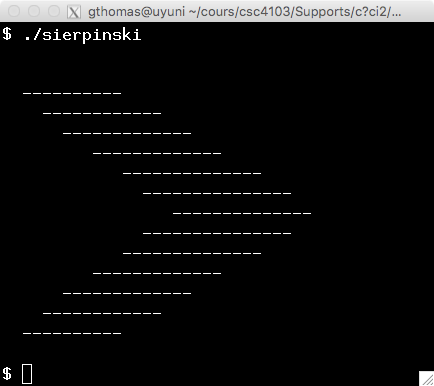
Par exemple, le polygone représenté sur l'illustration est défini par les points
(2, 13), (10, 13), (30, 7), (10, 1), (2, 1), (18, 7).
|
|
| a. Le polygone plein | b. Balayage de l'axe 9 |
Nous commençons par mettre en place la définition d'un polygone et l'algorithme de balayage.
Pour cela, vous devez :
- Définir une structure nommée point et contenant deux champs flottants nommés respectivement x et y.
- Écrire une fonction nommée plot_poly_sweep prenant en paramètre une grille, un tableau de points, le nombre de points du tableau, l'abscisse de l'axe balayé (un entier) et un pixel (un caractère). Pour le moment, cette fonction doit afficher l'axe balayé.
- Écrire une fonction nommée plot_poly et prenant en paramètre une grille, un tableau de points, le nombre de points du tableau et un pixel (un caractère). Cette fonction doit itérer avec une variable x sur les valeurs 0 à nb_columns() et appeler plot_poly_sweep pour chaque axe balayé.
- Supprimer de la fonction main la construction des lignes demandées dans la partie précédente, mais conserver la définition de la grille, son initialisation et son affichage.
- Créer un tableau de points nommé p dans la fonction main. Ce tableau doit être initialisé avec les points suivants : { 2, 13 }, { 10, 13 }, { 30, 7 }, { 10, 1 }, { 2, 1 }, { 18, 7 } (pensez à copier/coller cette ligne dans votre programme).
- Appeler la fonction plot_poly à partir de la fonction main, entre l'initialisation et l'affichage de la grille.
$ ./sierpinski
sweep 0:
sweep 1:
...
sweep 30:
sweep 31:
...
De façon à trouver les points d'intersections entre l'axe x balayé et les côtés du polygone,
nous allons itérer sur chaque côté du polygone dans la fonction plot_poly_sweep.
Techniquement, itérer sur les côtés du polygone revient à itérer sur l'ensemble des couples :
(p[n-1], p[0]), (p[0], p[1]), (p[1], p[2]), ..., (p[n-2], p[n-1]), où n est le nombre de points
du polygone.
À chaque itération, la variable j doit être égale à l'index de l'élément de gauche d'un couple
et la variable i à celui de droite.
Dans cette question, nous n'allons qu'afficher ces couples.
Pour cela, nous vous proposons de mettre en œuvre l'algorithme simple suivant :
L'affichage produit par votre programme devrait maintenant être similaire à celui-ci :
j prend la valeur de nombre de points - 1
Pour i va de 0 à nombre de points non inclus
affiche le couple (j, i)
j prend la valeur de i
Fin Pour
$ ./sierpinski
sweep 0: (5, 0) (0, 1) (1, 2) (2, 3) (3, 4) (4, 5)
sweep 1: (5, 0) (0, 1) (1, 2) (2, 3) (3, 4) (4, 5)
...
Pour chaque côté, nous souhaitons savoir si l'axe x traverse ce côté,
et en quel point :
- Pour savoir si l'axe x traverse le côté, il suffit de vérifier que x est bien compris entre p[i].x et p[j].x ou entre p[j].x et p[i].x.
- Pour connaître l'éventuel point d'intersection entre un côté et un axe x, un peu de géométrie de base s'impose. Si vous preniez le temps de poser le problème, vous trouveriez facilement (nous espérons) que ce point d'intersection n'est autre que p[i].y + (x - p[i].x) * (p[j].y - p[i].y) / (p[j].x - p[i].x) puisque la pente de la droite passant par p[i] et p[j] n'est autre que (p[j].y - p[i].x) / (p[j].x - p[i].x).
...
sweep 2: 13.000000 13.000000 1.000000 1.000000
sweep 3: 12.625000 13.000000 1.000000 1.375000
...
sweep 9: 10.375000 13.000000 1.000000 3.625000
sweep 10: 10.000000 13.000000 13.000000 1.000000 1.000000 4.000000
sweep 11: 9.625000 12.700000 1.300000 4.375000
...
sweep 28: 7.600000 6.400000
sweep 29: 7.300000 6.700000
sweep 30: 7.000000 7.000000
...
L'algorithme que vous venez de mettre œuvre n'est pas encore totalement correct car certains
points (les coins) apparaissent plusieurs fois. Dans certains cas, il faut effectivement qu'ils
apparaissent, dans d'autre, il ne faut pas (en particulier sur l'axe 10).
Toutefois, avant de corriger ce problème, nous allons dessiner les lignes verticales :
il est beaucoup plus commode de raisonner et de corriger un dessin plutôt qu'une série de points.
Avant de pouvoir dessiner nos lignes, il faut les trier. Pour cela, nous réutilisons
la fonction sort_insert définie à la première étape.
Modifiez votre fonction plot_poly_sweep de façon à :
- créer un tableau de n * 4 flottants nommés vlines non initialisé au début de la fonction (où n est le nombre de points passé en paramètre de la fonction),
- définir une variable nommée top servant à savoir combien de points se trouvent actuellement dans ce tableau,
- retirer l'affichage du point d'intersection et le remplacer par l'ajout du point d'intersection dans le tableau vlines avec la fonction sort_insert,
- afficher les points se trouvant dans le tableau après la boucle qui itère sur chaque côté. Vous devriez obtenir le même affichage que précédemment.
Nous pouvons maintenant dessiner le polygone. Après l'affichage des points d'intersections,
dessinez les lignes en prenant deux à deux les points du tableau.
Typiquement, si les points d'intersections sont { 1, 1.375, 12.625, 13 }, il faut
afficher les verticales [1, 1.375] et [12.625, 13] sur l'axe des x.
Vous pouvez remarquer que votre polygone est presque correct, sauf pour l'axe
10, dans lequel certaines lignes verticales se sont inversées:
----------
------ -----
---- --------
-------------
- --------------
- ---------------
- --------------
- ---------------
- --------------
-------------
---- --------
------ -----
----------
Nous corrigeons maintenant le problème de l'axe 10.
Le problème est que les points 1 et 13 apparaissent deux fois au lieu d'une.
Pour le point 1, par exemple, ce phénomène est
du au fait que l'axe 10 coupe la droite allant de (30, 7) à (10, 1), mais aussi
celle allant de (10, 1) à (2, 1).
De façon à ne compter qu'une unique fois ces points, il suffit de couper
le plan entre [0, x] et ]x, nb_columns()] : si
[p[i].x, p[j].x] coupe la partie droite du plan, on compte l'intersection, sinon, on l'ignore.
Pour le cas du point 1, on va donc compter le côté allant de (30, 7) à (10, 1),
mais pas celui allant de (2, 1) à (10, 1).
On peut reformuler cet invariant de la façon suivante :
- Si p[i].x <= p[j].x, alors on considère une intersection si p[i].x <= x et x < p[j].x,
- Si p[i].x >= p[j].x, alors on considère une intersection si p[i].x > x et x >= p[j].x
----------
------------
-------------
-------------
--------------
---------------
-------------
---------------
--------------
-------------
-------------
------------
----------
optionnel
Notre polygone est presque correct. Toutefois, certains coins ne sont plus dessinés,
en particulier le point (30, 7) puisque les côtés associés à ce point se trouvent à gauche dans
le plan. De la même façon, une droite verticale se trouvant à droite de la figure ne serait
plus dessinée. On peut se satisfaire de ce résultat si la résolution est grande.
Toutefois, si vous voulez corriger ce problème, vous pouvez enrichir légèrement votre algorithme
en dessinant les points et droites manquants dans la boucle qui itère
sur les côtés :
- Si p[i].x est égal à x, alors
- Si p[j].x est égal à x, nous sommes dans le cas d'un côté vertical. Nous dessinons directement ce côté en utilisant plot_vline. Pensez à considérer le cas où p[i].y < p[j].y et le cas inverse car plot_vline doit recevoir les arguments fy1 et fy2 dans l'ordre.
- Sinon, nous sommes dans le cas d'un coin. Nous dessinons directement le point en utilisant plot_vline de façon à dessiner une droite allant de p[i].y à p[i].y.
- Ensuite, que p[i].x soit on non égal à x, on s'occupe d'ajouter le point d'intersection comme dans la question précédente.
Le triangle (∼ 20mn, optionnel)
Étant maintenant capable de dessiner des polygones, nous pouvons enfin dessiner ce triangle
de Sierpiński.
Écrivez une fonction plot_triangle prenant en paramètre
une grille, trois points p1, p2 et p3
et un pixel. Cette fonction doit afficher le triangle plein en utilisant
plot_poly.
Supprimez les affichages effectués dans la fonction plot_poly.
Supprimez aussi les anciens tests de votre fonction main.
Enfin, modifiez la taille de votre grille pour avoir 65 lignes et 129 colonnes
et dessinez un triangle plein ayant pour coordonnées
(0, 0), (64, 64), (128, 0).
Comme il va falloir trouver les milieux des côtés des triangles, écrivez une fonction
nommé line_middle prenant en paramètre deux points et renvoyant
le point se trouvant au milieu du segment.
Pour finir, écrivez une fonction récursive sierpinski
prenant en paramètre une grille, trois points, un nombre n d'itération restant
et un pixel.
Cette fonction doit afficher le triangle si n est égal
à 1, sinon, cette fonction doit appeler trois fois sierpinski
avec comme argument chacun des triangles pleins restant à l'étape n-1.
Testez votre fonction avec 6 itérations.
Félicitation ! Vous venez d'écrire votre premier moteur graphique !

