Analyse des besoins et cas d'utilisation
- réponses
Instructions pour le QCM :
Pour chacune des questions, plusieurs réponses peuvent être
correctes, vous pouvez donc cocher plusieurs cases !
Les questions sont de trois niveaux de difficultés. Les niveaux
« intermédiaire » et « difficile » sont précédés
des signes « * » et « ** », respectivement.
-
L'affirmation suivante est-elle correcte ? Une association
binaire est une association bidirectionnelle.
| FAUX :
OUI
(
Le terme « binaire » indique le nombre de
classes liées par l'association. Le terme
« bidirectionnelle » concerne la navigabilité.
) |
| VRAI :
NON
(
Le terme « binaire » indique le nombre de
classes liées par l'association. Le terme
« bidirectionnelle » concerne la navigabilité.
) |
-
L'affirmation suivante est-elle correcte ? Pour une association,
le sens de lecture et la navigabilité sont deux concepts distincts.
| VRAI :
OUI
(
Le sens de lecture permet de prendre le nom de la classe d'origine
comme sujet, le nom de l'association comme proposition verbale, et le
nom de la classe destinatrice comme complément d'objet direct. La
navigabilité contraint le parcours de l'association.
) |
| FAUX :
NON
(
Le sens de lecture permet de prendre le nom de la classe d'origine
comme sujet, le nom de l'association comme proposition verbale, et le
nom de la classe destinatrice comme complément d'objet direct. La
navigabilité contraint le parcours de l'association.
) |
-
Voici le diagramme de classes utilisé par les questions qui suivent.
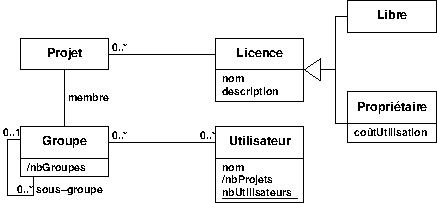
Un projet ne possède qu'une et une seule licence.
| VRAI :
Vrai.
(
La non-spécification explicite d'une multiplicité correspond à une
multiplicité implicite de valeur 1.
) |
| FAUX :
Faux.
(
La non-spécification explicite d'une multiplicité correspond à une
multiplicité implicite de valeur 1.
) |
-
Le libellé « sous-groupe » est-il un nom d'association ou un
nom de rôle ?
| FAUX :
Un nom d'association.
(
Tel que positionné volontairement à une extrémité de l'association,
« sous-groupe » est un nom de rôle.
) |
| VRAI :
Un nom de rôle.
(
Tel que positionné volontairement à une extrémité de l'association,
« sous-groupe » est un nom de rôle.
) |
-
Un groupe peut-il exister sans être inclus dans un groupe ?
| FAUX :
Vrai.
(
La cardinalité de l'association réflexive du côté opposé au nom de
rôle « sous-membre » autorise qu'un objet de classe
« Groupe » ne soit relié à aucun groupe. D'ailleurs, si la
cardinalité minimum était « 1 » alors le diagramme de
classes serait sans doute incohérent car comment concevoir que tout
groupe soit un sous-groupe d'un autre, sans racine. Il est possible de
dessiner un tel diagramme mais quelle serait sa signification dans ce
problème ?
) |
| VRAI :
Faux.
(
La cardinalité de l'association réflexive du côté opposé au nom de
rôle « sous-membre » autorise qu'un objet de classe
« Groupe » ne soit relié à aucun groupe. D'ailleurs, si la
cardinalité minimum était « 1 » alors le diagramme de
classes serait sans doute incohérent car comment concevoir que tout
groupe soit un sous-groupe d'un autre, sans racine. Il est possible de
dessiner un tel diagramme mais quelle serait sa signification dans ce
problème ?
) |
-
Un utilisateur peut-il appartenir à plusieurs groupes ?
| VRAI :
Vrai.
(
La cardinalité maximum du côté de la classe « Groupe » est
supérieure à « 1 ».
) |
| FAUX :
Faux.
(
La cardinalité maximum du côté de la classe « Groupe » est
supérieure à « 1 ».
) |
-
Le diagramme de classes permet-il de répondre à la question
suivante : quels sont les utilisateurs travaillant sur des
projets ayant une licence dite libre ?
| VRAI :
Vrai.
(
Le diagramme de classes définit un graphe permettant d'atteindre les
objets de la classes « Utilisateur » à partir de l'objet de
la classe « Libre », ceci via les objets des classes
« Projet », puis « Groupe ». Pour atteindre ces
objets de la classe « Utilisateur », les quatre associations
doivent pouvoir être parcourues.
) |
| FAUX :
Faux.
(
Le diagramme de classes définit un graphe permettant d'atteindre les
objets de la classes « Utilisateur » à partir de l'objet de
la classe « Libre », ceci via les objets des classes
« Projet », puis « Groupe ». Pour atteindre ces
objets de la classe « Utilisateur », les quatre associations
doivent pouvoir être parcourues.
) |
-
Soit quatre instances de la classe
« Utilisateur ». Considérons que les seuls attributs sont
ceux spécifiés dans le diagramme et qu'un attribut occupe une case
mémoire. Faut-il 8 cases mémoire pour stocker les attributs des quatre
instances ?
| FAUX :
Vrai.
(
L'attribut « nbUtilisateurs » est un attribut de classe. Il
est donc partagé entre les instances et ne constitue qu'une case
mémoire. Donc, pour les quatre instances, nous avons besoin de 9 cases
mémoire : 2 fois 4 pour les attributs d'instance + 1 pour l'attribut
de classe.
) |
| VRAI :
Faux.
(
L'attribut « nbUtilisateurs » est un attribut de classe. Il
est donc partagé entre les instances et ne constitue qu'une case
mémoire. Donc, pour les quatre instances, nous avons besoin de 9 cases
mémoire : 2 fois 4 pour les attributs d'instance + 1 pour l'attribut
de classe.
) |
-
L'attribut « nbProjets » de la classe
« Utilisateur » est-il un attribut dérivé ?
| VRAI :
Vrai.
(
C'est la signification du signe « / » devant le nom de
l'attribut.
) |
| FAUX :
Faux.
(
C'est la signification du signe « / » devant le nom de
l'attribut.
) |
-
Un objet licence de type « Libre » est-il une
« Licence » ?
| VRAI :
Vrai.
(
C'est ce qu'exprime la généralisation spécialisation.
) |
| FAUX :
Faux.
(
C'est ce qu'exprime la généralisation spécialisation.
) |
-
Soit deux instances de la classe « Libre » et deux instances
de la classe « Propriétaire ». Considérons que les seuls
attributs sont ceux spécifiés dans le diagramme et qu'un attribut
occupe une case mémoire. Le nombre de cases mémoire nécessaires pour
stocker les attributs des quatre instances est 10.
| VRAI :
Vrai.
(
Les attributs « nom » et « description » sont des
attributs de la classe parente. Les classes enfant les contiennent donc
aussi. Donc, pour les quatre instances, nous avons besoin de 10 cases
mémoire : 2 fois 4 pour les attributs de la classe parent + 2
fois 2 pour l'attribut spécifique aux deux instances de la classe
« Propriétaire ».
) |
| FAUX :
Faux.
(
Les attributs « nom » et « description » sont des
attributs de la classe parent. Les classes enfant les contiennent donc
aussi. Donc, pour les quatre instances, nous avons besoin de 10 cases
mémoire : 2 fois 4 pour les attributs de la classe parent + 2
fois 2 pour l'attribut spécifique aux deux instances de la classe
« Propriétaire ».
) |
-
Voici le diagramme d'objets utilisé par les questions qui suivent.
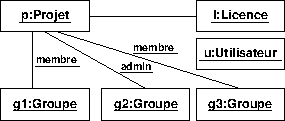
« p » est-il un objet ?
| VRAI :
Vrai.
|
| FAUX :
Faux.
|
-
La multiplicité de l'association « membre » du côté de la
classe « Groupe » peut-elle être « 0..2 » ?
| VRAI :
Vrai.
(
Le diagramme d'objets montre qu'un projet peut avoir deux groupes de
membres. Donc, la multiplicité maximum du côté de la classe
« Groupe » peut être « 2 ».
) |
| FAUX :
Faux.
(
Le diagramme d'objets montre qu'un projet peut avoir deux groupes de
membres. Donc, la multiplicité maximum du côté de la classe
« Groupe » peut être « 2 ».
) |
-
La multiplicité de l'association « membre » du côté de la
classe « Groupe » peut-elle être « 1..2 » ?
| VRAI :
Vrai.
(
La présence d'une instance d'association peut montrer que la
multiplicité maximum est supérieure à « 0 » (ici 2). Elle ne
dit rien sur la multiplicité minimum. Donc, la multiplicité minimum
« 1 » peut être acceptée comme contrainte.
) |
| FAUX :
Faux.
(
La présence d'une instance d'association peut montrer que la
multiplicité maximum est supérieure à « 0 » (ici 2). Elle ne
dit rien sur la multiplicité minimum. Donc, la multiplicité minimum
« 1 » peut être acceptée comme contrainte.
) |
-
UML interdit qu'un objet soit associé deux fois avec un autre objet
par la même association. Dans notre exemple, est-il interdit qu'un
objet « Groupe » soit associé deux fois avec le même objet
« Projet » par l'association « membre » ?
| VRAI :
Vrai.
(
Par définition, une association relie un objet de chaque extrémité au
plus une fois. Par conséquent, un même objet « Groupe » est
associé au maximum une fois à un objet « Projet » par
l'association « membre ».
) |
| FAUX :
Faux.
(
Par définition, une association relie un objet de chaque extrémité au
plus une fois. Par conséquent, un même objet « Groupe » est
associé au maximum une fois à un objet « Projet » par
l'association « membre ».
) |

